Chapter 13 Trigonometric Identities
Class 10th R. S. Aggarwal Maths Solution
CBSE Class 10 Maths
R. S. Aggarwal Solution
Trigonometric Identities Exercise Ex. 13A
Solution 1
L.H.S = sin4θ - cos4θ
= (sin2θ)2 - (cos2θ)2
= (sin2θ - cos2θ) (sin2θ + cos2θ) … ∵ a2 - b2 = (a - b)(a + b)
= 1 (sin2θ - cos2θ) …. ∵ sin2θ + cos2θ = 1
= 1 - cos2θ - cos2θ …. ∵ sin2θ = 1 - cos2θ
= 1 - 2 cos2θ
= R.H.S
Hence proved.
Solution 2
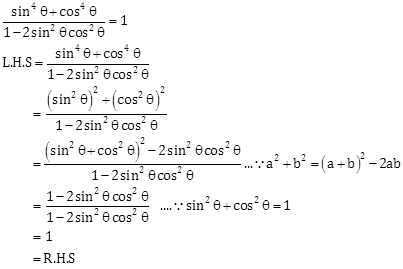
Hence proved.
Solution 3
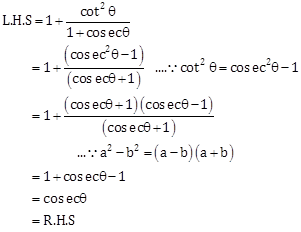
Hence proved.
Solution 4

Hence proved.
Solution 5
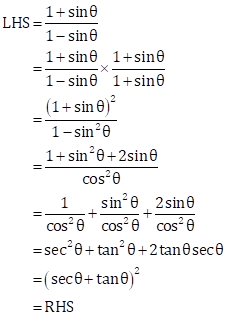
Solution 6

Hence proved.
Solution 7
L.H.S = sec4 θ - tan4 θ
= (sec2 θ)2 - (tan2 θ)2
= (sec2 θ - tan2 θ) (sec2 θ + tan2 θ)
= 1 × (sec2 θ + tan2 θ) …. ∵ sec2 θ - tan2 θ = 1
= 1 + tan2 θ + tan2 θ …. ∵ sec2 θ = 1 + tan2 θ
= 1 + 2 tan2 θ
= R.H.S
Hence proved.
Solution 8
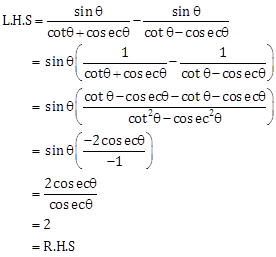
Hence proved.
Solution 9
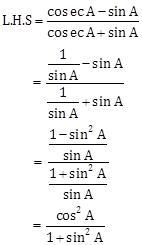
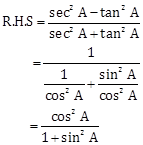
∵ L.H.S = R.H.S
![]()
Hence proved.
Solution 10
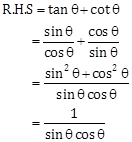
∵ L.H.S = R.H.S
⇒ sin2 θ tan θ + cos2 θ cot θ + 2 sin θ cos θ = tan θ + cot θ
Solution 11
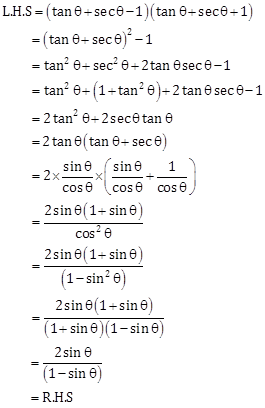
Hence proved.
Solution 12
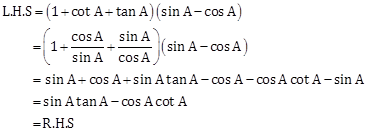
Hence proved.
Solution 13
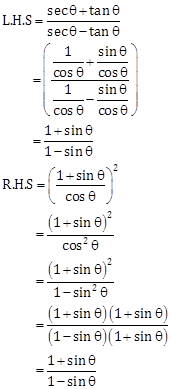
∵ L.H.S = R.H.S
⇒ ![]()
Solution 14
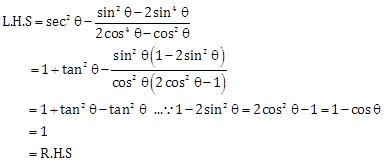
Hence proved.
Solution 15

Solution 16
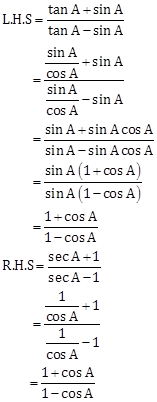
∵ L.H.S = R.H.S
![]()
Solution 17
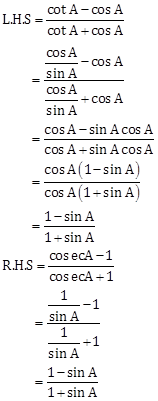
∵ L.H.S = R.H.S
![]()
Solution 18
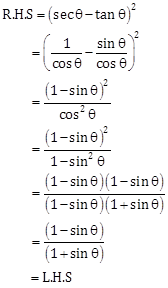
Hence proved.
Solution 19
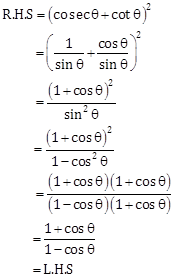
Hence proved.
Solution 20
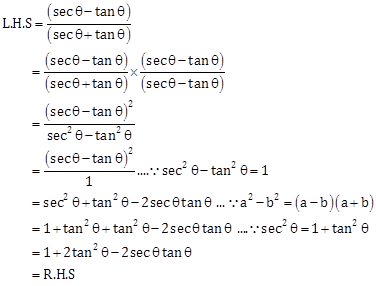
Hence proved.
Solution 21
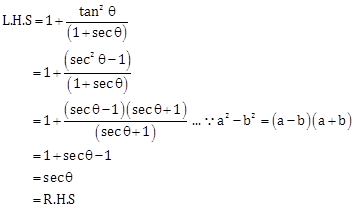
Hence proved.
Solution 22
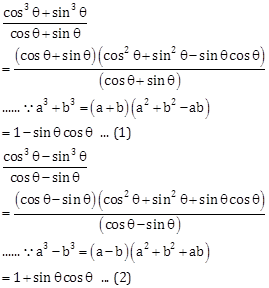
From (1) and (2), we get
L.H.S = ![]()
= 1 - sin θ cos θ + 1 + sin θ cos θ
= 2
= R.H.S
Hence proved.
Solution 23
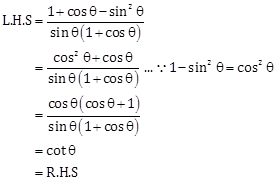
Hence proved.
Solution 24
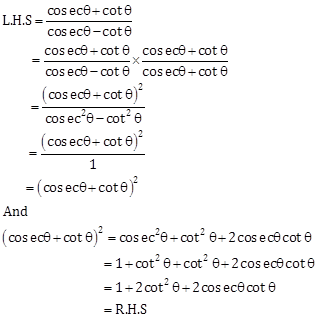
Hence proved.
Solution 25

Hence proved.
Solution 26

Hence proved.
Solution 27
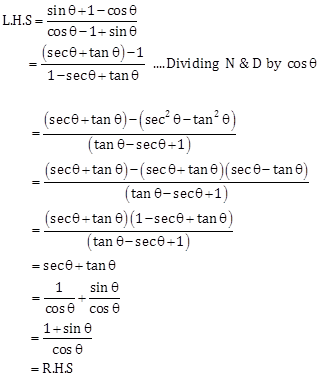
Solution 28
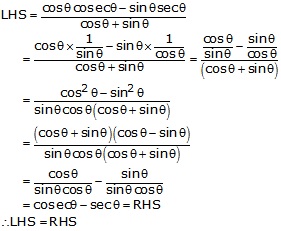
Solution 29

Solution 30

Solution 31(i)
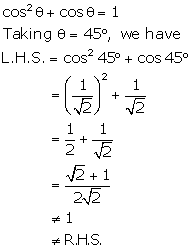
Solution 31(ii)
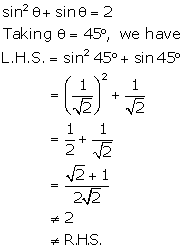
Solution 31(iii)
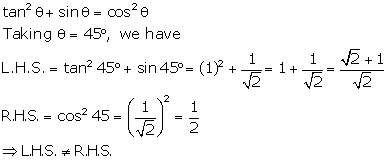
Trigonometric Identities Exercise Ex. 13B
Solution 1
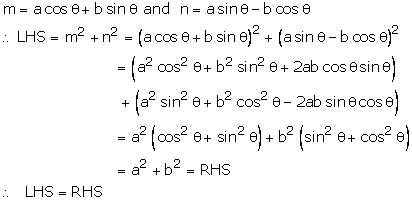
Solution 2
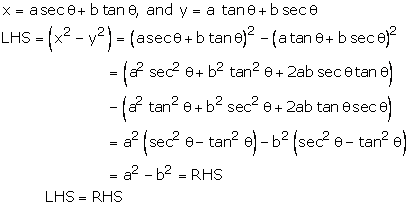
Solution 3
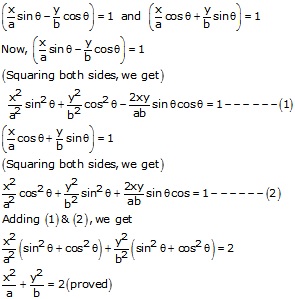
Solution 4

Solution 5
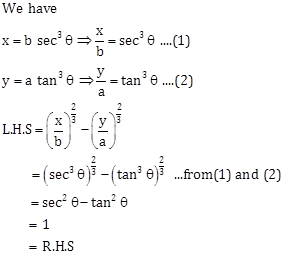
Hence proved.
Solution 6
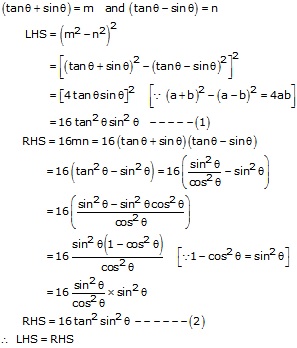
Solution 7

Solution 8
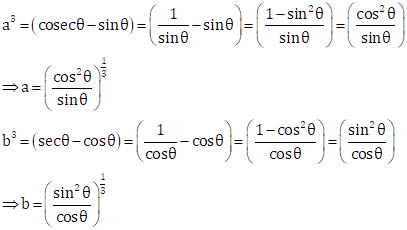
Now,
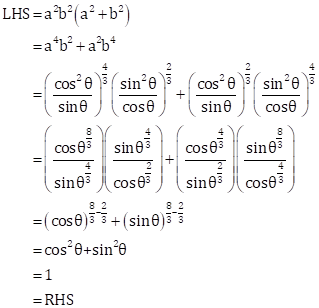
Solution 9
We have,
x = (sec A + sin A) and y = (sec A - sin A)
⇒ x + y = 2 sec A ⇒ sec A = ![]() ⇒
cos A =
⇒
cos A = ![]() …. (1)
…. (1)
And x - y = 2 sin A ⇒ sin A =
![]() ….. (2)
….. (2)
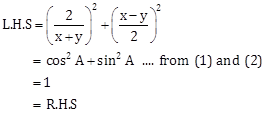
Solution 10
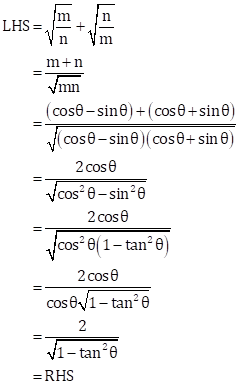
Solution 11
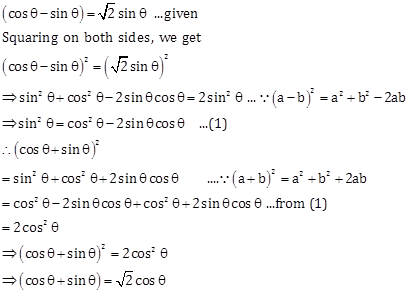
Hence proved.
Solution 12
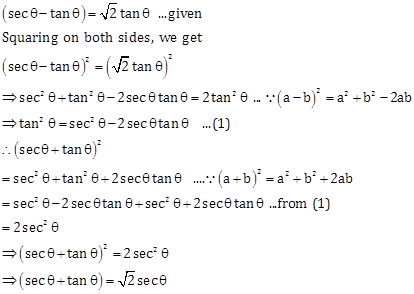
Hence proved.
Solution 13
We know that,
sec2 θ - tan2 θ = 1
⇒ (sec θ + tan θ) (sec θ - tan θ) = 1 … a2 - b2 = (a - b)(a + b)
⇒ p (sec θ - tan θ) = 1 …. ∵ (sec θ + tan θ) = p
⇒ (sec θ - tan θ) = ![]()
We have,
(sec θ + tan θ) = p …. (1) and (sec θ - tan θ) = ![]() …. (2)
…. (2)
Adding (1) and (2), we get
2 sec θ = ![]() ⇒ cos θ =
⇒ cos θ = ![]() …. (3)
…. (3)
Subtracting (2) from (1), we get
2 tan θ = ![]()
⇒ tan θ ![]()
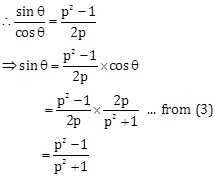
Solution 14

Hence proved.
Solution 15

Hence proved.
Solution 16
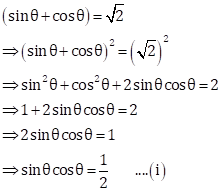
Now,
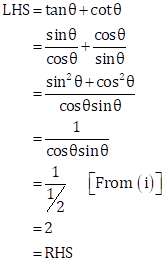
Trigonometric Identities Exercise MCQ
Solution 1
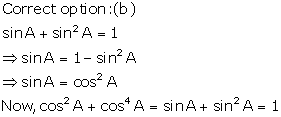
Solution 2
Correct Option: (c)
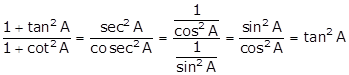
Solution 3
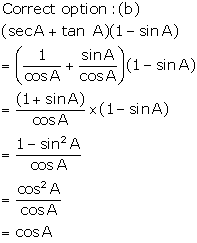
Solution 4
Correct Option: (d)
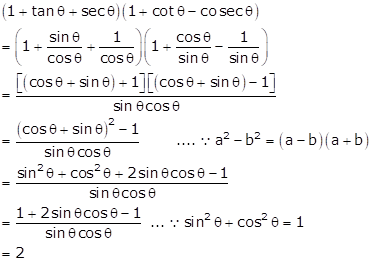
Solution 5
Correct Option: (b)
sin θ - cos θ = 0 …. Given
⇒ (sin θ - cos θ)2 = sin2 θ + cos2 θ - 2 sin θ cos θ
⇒ 0 = 1 - 2 sin θ cos θ …. ∵ sin2 θ + cos2 θ = 1
⇒ 2 sin θ cos θ = 1
⇒ sin θ cos θ = ![]()
⇒ sin2 θ cos2 θ = ![]()
∴ sin4 θ + cos4 θ
= (sin2 θ + cos2 θ)2 - 2 sin2 θ cos2 θ
= ![]()
Solution 6
Correct Option: (c)
cos 9α = sin α
⇒ sin(90˚- 9α) = sin α
∴ 90˚- 9α = α ⇒ 10α = 90˚ ⇒ α = 9˚
∴ tan 5α = tan 5(9˚) = tan 45˚ = 1
Solution 7
Correct Option: (d)
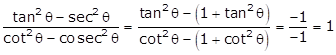
Solution 8
Correct option: (a)
Solution 9
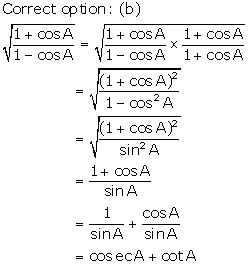
Solution 10
Correct Option: (b)
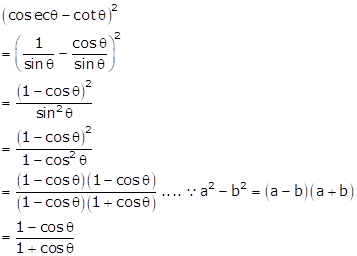
Solution 11
Correct option: (a)
Solution 12

Solution 13

Solution 14
Correct Option: (a)
![]()
cosec2 θ = 1 + cot2 θ = ![]()
∴ ![]()
Solution 15
Correct Option: (c)
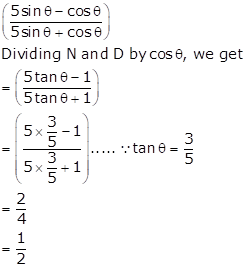
Solution 16
Correct Option: (a)
In a ∆ABC, ∠C = 90˚ ⇒ ∠A + ∠B = 90˚
∴ cos(A + B) = cos 90˚ = 0
Solution 17
Correct Option: (a)
We have, cos A + cos2 A = 1 … (1)
⇒ cos A = 1 - cos2 A = sin2 A ⇒ sin4 A = cos2 A
∴ (sin2 A + sin4 A) = cos A + cos2 A = 1 …from (1)
Solution 18

Solution 19
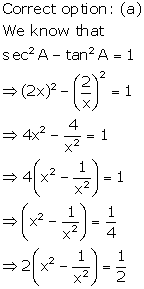
Solution 20
Correct option: (c)
We know that
cosec2 x - cot2 x = 1
Solution 21