Chapter 12 Trigonometric Ratios of Complementary Angles
Class 10th R. S. Aggarwal Maths Solution
CBSE Class 10 Maths
R. S. Aggarwal Solution
Trigonometric Ratios of Complementary Angles Exercise Ex. 12
Solution 1(i)
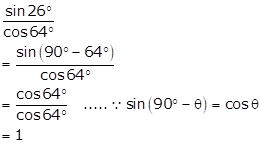
Solution 1(ii)
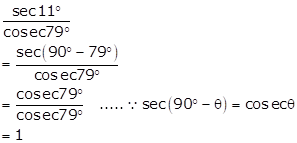
Solution 1(iii)
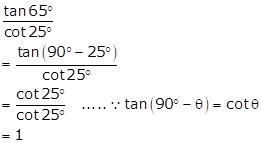
Solution 1(iv)
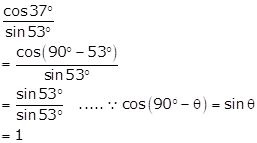
Solution 1(v)
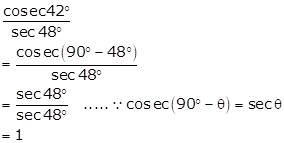
Solution 1(vi)
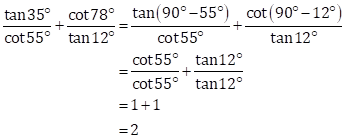
Solution 2(i)
L.H.S = cos81˚ - sin9˚
= cos(90˚- 9˚) - sin9˚
= sin9˚ - sin9˚ ….. ∵ cos(90˚- θ) = sin θ
= 0
= R.H.S
Hence proved.
Solution 2(ii)
L.H.S = tan71˚ - cot19˚
= tan(90˚- 19˚) - cot19˚
= cot19˚ - cot19˚ ….. ∵ tan(90˚- θ) = cot θ
= 0
= R.H.S
Hence proved.
Solution 2(iii)
L.H.S = cosec60˚ - sec30˚
= cosec(90˚- 30˚) - sec30˚
= sec30˚ - sec30˚ ….. ∵ cosec(90˚- θ) = sec θ
= 0
= R.H.S
Hence proved.
Solution 2(iv)
L.H.S = cot34˚ - tan56˚
= cot(90˚- 56˚) - tan56˚
= tan56˚ - tan56˚ ….. ∵ cot(90˚- θ) = tan θ
= 0
= R.H.S
Hence proved.
Solution 2(v)
L.H.S = sin2 48˚ + sin2 42˚
= sin2 (90˚- 42˚) + sin2 42˚
= cos2 42˚ + sin2 42˚ ….. ∵ sin(90˚- θ) = cos θ
= 1 ….. ∵ sin2 θ+ cos2θ= 1
= R.H.S
Hence proved.
Solution 2(vi)
L.H.S = cos2 72˚ + cos2 18˚
= cos2 (90˚- 18˚) + cos2 18˚
= sin2 18˚ + cos2 18˚ ….. ∵ cos(90˚- θ) = sin θ
= 1 ….. ∵ sin2 θ+ cos2θ= 1
= R.H.S
Hence proved.
Solution 3(i)
L.H.S = sin2 12˚ + sin2 78˚
= sin2 (90˚- 78˚) + sin2 78˚
= cos2 78˚ + sin2 78˚ ….. ∵ sin(90˚- θ) = cos θ
= 1 ….. ∵ sin2 θ+ cos2θ= 1
= R.H.S
Hence proved.
Solution 3(ii)
L.H.S = sec2 29˚- cot2 61˚
= sec2 29˚ - cot2 (90˚- 29˚)
= sec2 29˚ - tan229˚ ….. ∵ cot(90˚- θ) = tan θ
= 1 ….. ∵ sec2 θ - tan2θ= 1
= R.H.S
Hence proved.
Solution 3(iii)
L.H.S = tan2 56˚- cot2 34˚
= tan2 56˚- cot2 (90˚- 56˚)
= tan2 56˚- tan2 56˚ ….. ∵ cot(90˚- θ) = tan θ
= 0
= R.H.S
Solution 3(iv)
L.H.S = cos2 57˚ - sin2 33˚
= cos2 57˚ - sin2(90˚- 57˚)
= cos2 57˚ - cos2 57˚ ….. ∵ sin(90˚- θ) = cos θ
= 0
= R.H.S
Hence proved.
Solution 3(v)
L.H.S = sec2 50˚- cot2 40˚
= sec2 50˚ - cot2 (90˚- 50˚)
= sec2 50˚ - tan250˚ ….. ∵ cot(90˚- θ) = tan θ
= 1 ….. ∵ sec2 θ - tan2θ= 1
= R.H.S
Hence proved.
Solution 3(vi)
L.H.S = cosec2 72˚ - tan2 18˚
= cosec2 72˚ - tan2 (90˚- 72˚)
= cosec2 72˚ - cot2 72˚ ….. ∵ tan(90˚- θ) = cot θ
= 1 ….. ∵ cosec2 θ - cot2θ= 1
= R.H.S
Hence proved.
Solution 4(i)
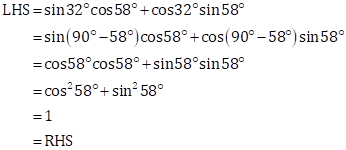
Solution 4(ii)

Solution 4(iii)
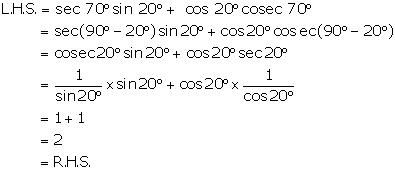
Solution 4(iv)
L.H.S = tan15˚ tan60˚ tan75˚
= (tan15˚ tan75˚) tan60˚
= [tan 15˚tan(90˚- 15˚)] tan60˚
= (tan 15˚cot 15˚) tan60˚ ……∵ tan(90˚- θ) = cot θ
= (tan 15˚×1/tan15˚) tan60˚ …… ∵ cot θ = 1/tan θ
= 1 × √3
= √3
= R.H.S
Hence proved.
Solution 4(v)
L.H.S = tan48˚ tan23˚ tan42˚ tan67˚ tan45˚
= (tan48˚ tan42˚) (tan23˚ tan67˚) tan45˚
= [tan 48˚tan(90˚- 48˚)] [tan 23˚tan(90˚- 23˚)] tan45˚
= (tan 48˚cot 48˚) (tan 23˚cot 23˚) tan45˚
……∵ tan(90˚- θ) = cot θ
= (tan 48˚×1/tan 48˚) (tan 23˚×1/tan 23˚) tan45˚
…… ∵ cot θ = 1/tan θ
= 1×1×1
= 1
= R.H.S
Hence proved.
Solution 4(vi)
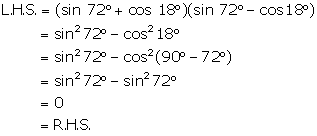
Solution 4(vii)
L.H.S = cosec 39˚cos51˚ + tan21˚ cot 69˚- sec2 21˚
= cosec 39˚cos(90˚- 39˚) + tan 21˚cot(90˚- 21˚) - sec2 21˚
= cosec 39˚sin 39˚+ tan 21˚tan 21˚- sec2 21˚
….. ∵ cot(90˚- θ) = tan θ and cos(90˚- θ) = sin θ
= 1 + tan221˚- sec2 21˚
= 1 - (sec2 21˚- tan221˚)
= 1 - 1 ……. ∵ sec2 θ - tan2θ = 1
= 0
= R.H.S
Hence proved.
Solution 5(i)
sin 72˚ + cosec 72˚
= sin(90˚- 18˚) + cosec(90˚- 18˚)
= cos 18˚+ sec 18˚
Solution 5(ii)
cosec 66˚ + tan 66˚
= cosec(90˚- 24˚) + tan(90˚- 24˚)
= sec 24˚+ cot 24˚
Solution 5(iii)
tan 68˚ + sec 68˚
= tan(90˚- 22˚) + sec(90˚- 22˚)
= cot 22˚+ cosec 22˚
Solution 5(iv)
cot 59˚ + cosec 59˚
= cot(90˚- 31˚) + cosec(90˚- 31˚)
= tan 31˚+ sec 31˚
Solution 5(v)
cos 51˚ + cot 49˚ - sec 47˚
= cos(90˚- 39˚) + cot(90˚- 41˚) - sec(90˚- 43˚)
= sin 39˚+ tan 41˚- cosec 43˚
Solution 5(vi)
sin 67˚ + cos 75˚
= sin(90˚- 23˚) + cos(90˚- 15˚)
= cos 23˚+ sin 15˚
Solution 6
sin 3A = cos (A - 10˚)
⇒ cos(90˚- 3A) = cos (A - 10˚) = ….. ∵ cos(90˚ - θ) = sin θ
∴ 90˚- 3A = A - 10˚
⇒ 4A = 100˚
⇒ A = 25˚
Solution 7
tan A = cot (A + 10˚)
⇒ cot(90˚- A) = cot(A + 10˚) = ….. ∵ cot(90˚ - θ) = tan θ
∴ 90˚- A = A + 10˚
⇒ 2A = 80˚
⇒ A = 40˚
Solution 8
cos 2A = sin (A - 15˚)
⇒ sin(90˚- 2A) = sin (A - 15˚) = ….. ∵ sin(90˚ - θ) = cos θ
∴ 90˚- 2A = A - 15˚
⇒ 3A = 105˚
⇒ A = 35˚
Solution 9
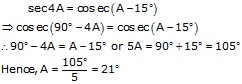
Solution 10
tan 2θ = cot (θ + 6˚)
⇒ cot (θ + 6˚) = cot(90˚- 2θ) ….. ∵ cot(90˚- θ) = tan θ
∴ θ + 6˚= 90˚- 2θ
⇒ 3θ = 84˚
⇒ θ = 28˚
Solution 11
sin (θ + 36˚) = cos θ
⇒ sin (θ + 36˚) = sin(90˚- θ) ….. ∵ sin(90˚ - θ) = cos θ
∴ θ + 36˚= 90˚- θ
⇒ 2θ = 54˚
⇒ θ = 27˚
Solution 12
3 cot 31˚tan 15˚cot 27˚tan 75˚cot 63˚cot 59˚
= 3 (cot 31˚cot 59˚)(tan 15˚tan 75˚)(cot 27˚cot 63˚)
= 3 [cot 31˚cot (90˚- 31˚)] [tan 15˚tan (90˚- 15˚)] [cot 27˚cot (90˚- 27˚)]
= 3 (cot 31˚tan 31˚)(tan 15˚cot 15˚)(cot 27˚tan 27˚)
….. ∵ tan(90˚- θ) = cot θ and cot(90˚- θ) = tan θ
= 3 …..∵ tan θ = 1/ cot θ and cot θ = 1/ tan θ
Solution 13
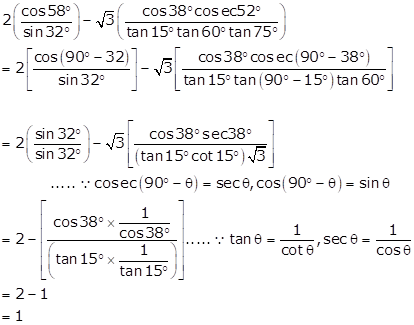
Solution 14
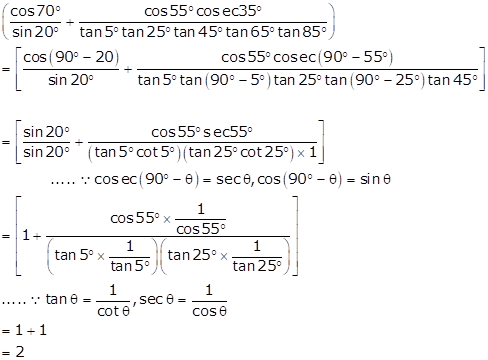
Solution 15
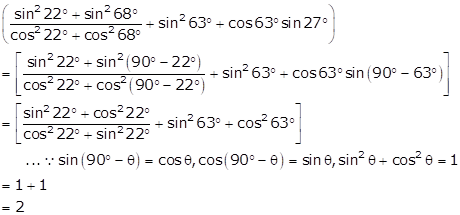
Solution 16
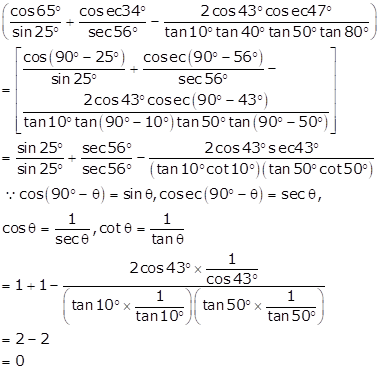
Solution 17
cot θ tan(90˚- θ) - sec(90˚- θ) cosec θ + sin2 65˚+ sin2 25˚+ √3 tan 5˚ tan 45˚ tan 85˚
= cot θ cot θ - cosec θ cosec θ + sin2 (90˚- 25˚)+ sin2 25˚+ √3 (tan 5˚ tan 85˚) tan 45˚
= (cot2θ - cosec2θ) + (cos2 25˚+ sin2 25˚) + √3 [tan 5˚ tan (90˚- 5˚) × 1
= - 1 + 1 + √3 (tan 5˚cot 5˚)
= 0 + √3
(tan 5˚× ![]() )
)
= √3
Solution 18
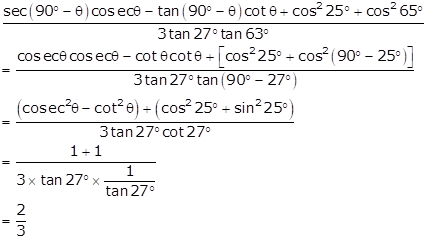
Solution 19
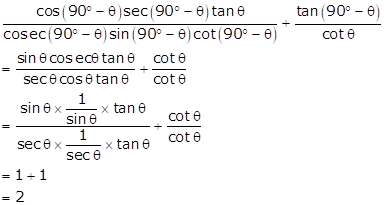
Solution 20
sin(50˚+ θ) - cos(40˚- θ) + tan1˚tan10˚tan20˚tan70˚tan80˚ tan89˚
= cos [90˚- (50˚- θ)] - cos(40˚- θ) + (tan1˚tan89˚) (tan10˚tan80˚) (tan20˚tan70˚) ….. ∵ sin θ = cos(90˚- θ)
= cos(40˚- θ)] - cos(40˚- θ) + [tan1˚tan(90˚- 1˚)] [tan10˚tan(90˚- 10˚)] [tan20˚tan(90˚- 20˚)]
= 0 + (tan1˚cot1˚)( tan10˚cot10˚)( tan20˚cot20˚) … ∵ tan(90˚- θ)= cot θ
= 1 × 1 × 1 …….∵ tan θ = ![]()
= 1
Solution 21
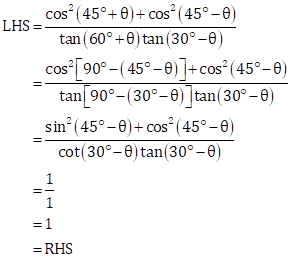
Trigonometric Ratios of Complementary Angles Exercise MCQ
Solution 1
Correct Option: (d)
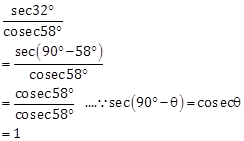
Solution 2
Correct Option: (c)
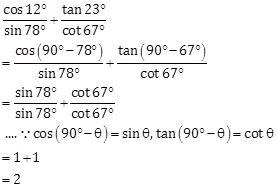
Solution 3
Correct Option: (b)
tan 10˚ tan 15˚ tan 75˚ tan 80˚
= tan 10˚ tan (90˚- 10˚) tan 15˚ tan (90˚- 15˚)
= (tan 10˚ cot 10˚)( tan 15˚ cot 15˚) ……∵ tan (90˚- θ) = cot θ
= (tan 10˚ × 1/tan 10˚)( tan 15˚× 1/tan 15˚) …∵ cot θ = 1/ tan θ
= 1
Solution 4
Correct Option: (c)
tan 5˚ tan 25˚ tan 30˚ tan 65˚ tan 85˚
= tan 5˚tan(90˚- 5˚) tan 25˚ tan(90˚- 25˚) tan 30˚
= (tan 5˚cot 5˚)( tan 25˚cot25˚) tan 30˚… ∵ tan (90˚- θ) = cot θ
= (tan 5˚× 1/tan
5˚)( tan 25˚× 1/tan
25˚) × ![]()
…… ∵ cot θ = 1/ tan θ
= ![]()
Solution 5
Correct Option: (a)
cos 1˚ cos 2˚ cos 3˚ …… cos 180˚
= cos 1˚ cos 2˚ cos 3˚ …… cos 90˚ ….. cos 180˚
= 0 ….. ∵ cos 90˚= 0
Solution 6
Correct Option: (b)
sin 43˚ cos 47˚ + cos 43˚ sin 47˚
= sin 43˚ cos(90˚ - 43˚) + cos 43˚ sin(90˚ - 43˚)
= sin 43˚ sin 43˚+ cos 43˚ cos 43˚ … ∵ cos(90˚- θ) = sin θ
= sin2 43˚+ cos2 43˚ …… ∵ sin2 θ + cos2 θ = 1
= 1
Solution 7
Correct Option: (c)
sec 70˚ sin 20˚ + cos 20˚ cosec 70˚
= sec (90˚- 20˚) sin 20˚ + cos 20˚ cosec (90˚- 20)
= cosec 20˚sin 20˚ + cos 20˚sec 20˚
…. ∵ sec (90˚- θ) = cosec θ, cosec (90˚- θ) = sec θ
= cosec 20˚× 1/cosec 20˚ + cos 20˚× 1/cos 20˚
…. ∵ sin θ = 1/ cosec θ, sec θ = 1/ cos θ
= 1 + 1
= 2
Solution 8
Correct Option: (a)
cosec2 57˚- tan2 33˚
= cosec2 57˚ - tan2 (90˚ - 57˚)
= cosec2 57˚ - cot2 57˚
= 1 …. ∵ cosec2 θ - cot2 θ = 1
Solution 9
Correct Option: (b)
sec2 10˚- cot2 80˚
= sec2 10˚ - cot2 (90˚ - 10˚)
= sec2 10˚ - tan2 10˚
= 1 …. ∵ sec2 θ - tan2 θ = 1
Solution 10
Correct Option: (d)
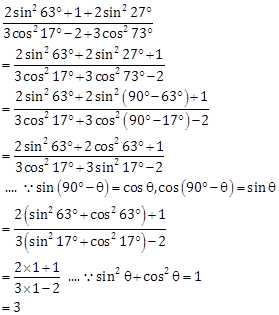
Solution 11
Correct Option: (a)
sin 38˚ - cos 52˚
= sin 38˚ - cos (90˚ - 38˚)
= sin 38˚- sin 38˚ …. ∵ cos (90˚ - θ) = sin θ
= 0
Solution 12
Correct Option: (b)
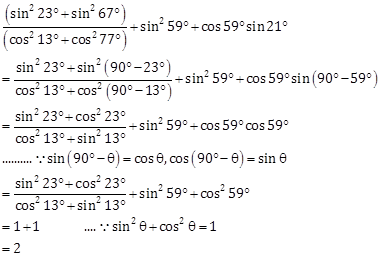
Solution 13
Correct Option: (c)
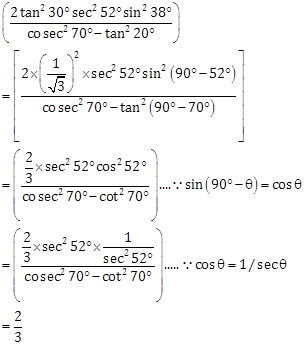
Solution 14
Correct Option: (b)
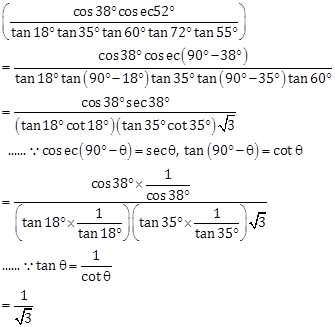
Solution 15
Correct Option: (c)
sin (60˚ + θ) - cos (30˚- θ)
= cos [90˚ - (60˚ + θ)] - cos (30˚- θ) …..∵ sin (90˚ + θ) = cos θ
= cos (30˚- θ) - cos (30˚- θ)
= 0
Solution 16
Correct Option: (d)
sin A = cos B
⇒ sin A = sin (90˚- B)
∴ A = 90˚- B ⇒ A + B = 90˚
Solution 17
Correct Option: (b)
cos (α + β) = 0
⇒ cos (α + β) = cos 90˚
∴ α + β = 90˚ ⇒ α = 90˚- β
∴ α - β = 90˚- β - β = 90˚- 2β
⇒ sin (α - β) = sin (90˚- 2β) = cos 2β … ∵ cos (90˚- θ) = sin θ
Solution 18
Correct Option: (a)
sin (45˚+ θ) - cos (45˚- θ)
= cos [90˚ - (45˚+ θ)] - cos (45˚- θ)
= cos (45˚- θ) - cos (45˚- θ) …. ∵ cos (90˚- θ) = sin θ
= 0
Solution 19
Correct Option: (a)
sec 4A = cosec (A - 10˚)
⇒ cosec (90˚ - 4A) = cosec (A - 10˚) ….∵ cosec (90˚ - θ) = sec θ
∴ 90˚ - 4A = A - 10˚
⇒ 5A = 100˚
⇒ A = 20˚
Solution 20
Correct Option: (c)
sin 3A = cos (A - 10˚)
⇒ cos (90˚ - 3A) = cos (A - 10˚) …. ∵ cos (90˚ - θ) = sin θ
∴ 90˚ - 3A = A - 10˚
⇒ 4A = 100˚
⇒ A = 25˚
Solution 21(i)
cot 34˚- tan 56˚
= cot (90˚- 56˚) - tan 56˚
= tan 56˚- tan 56˚ …. ∵ cot (90˚- θ) = tan θ
= 0
∴ cot 34˚- tan 56˚ = 0
Solution 21(ii)
cosec 31˚- sec 59˚
= cosec (90˚- 59˚) - sec 59˚
= sec 59˚- sec 59˚ …. ∵ cosec (90˚- θ) = sec θ
= 0
∴ cosec 31˚- sec 59˚ = 0
Solution 21(iii)
cos2 67˚+ cos2 23˚
= cos2 (90˚- 23˚) + cos2 23˚
= sin2 23˚ + cos2 23˚
= 1 ….. ∵ sin2 θ + cos2 θ = 1
∴ cos2 67˚+ cos2 23˚ = 1
Solution 21(iv)
cosec2 54˚- tan2 36˚
= cosec2 (90˚- 23˚) - tan2 36˚
= sin2 23˚ + cos2 23˚ …. ∵ cosec (90˚- θ) = sin θ
= 1 ….. ∵ sin2 θ + cos2 θ = 1
∴ cosec2 54˚- tan2 36˚ = 1
Solution 21(v)
sec2 40˚- cot2 50˚
= sec2 (90˚- 50˚) - cot2 50˚
= cosec2 50˚ - cot2 50˚
= 1 …. ∵ cosec2 50˚ - cot2 50˚ = 1
∴ sec2 40˚- cot2 50˚ = 1