ROUTERA

CBSE Chapter 8 Circles

Class 10th R. D. Sharma Maths Solution
CBSE Class 10 Maths
R. D. Sharma Solution

Circles Exercise Ex. 8.1

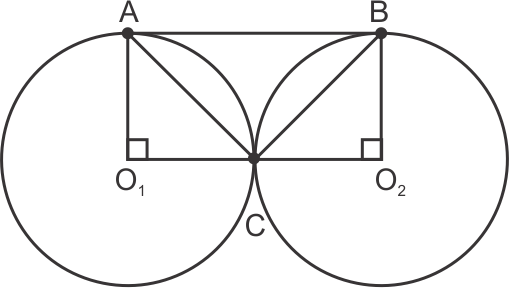
Solution 1

Fill in the blanks:

(i) The common point of a tangent and the circle is called point of contact .

(ii) A circle may have two parallel tangents.

(iii) A tangent to a circle intersects it in one point(s).

(iv) A line intesecting a circle in two points is called a secant .

(v) The angle between tangent at a point on a circle and the radius through the point is 90o .

Solution 2

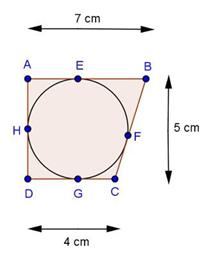
Solution 3

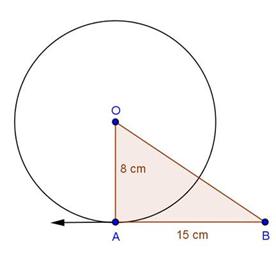
Solution 4

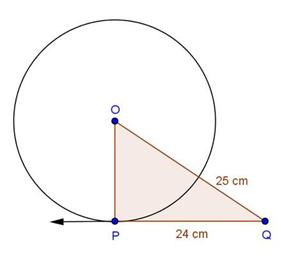
Circles Exercise Ex. 8.2

Solution 1

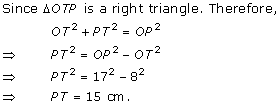
Solution 2

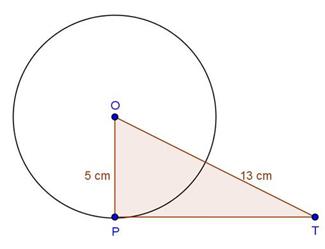
Solution 3

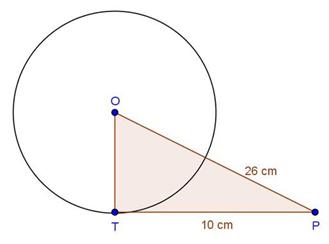
Solution 4

Solution 5

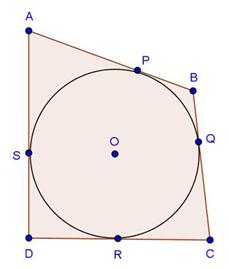
Solution 6

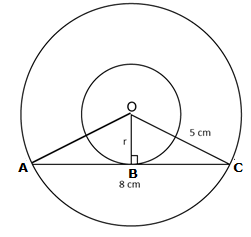
Solution 7

 

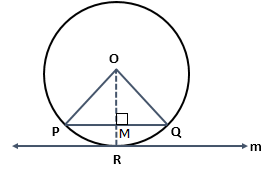
Solution 8

 

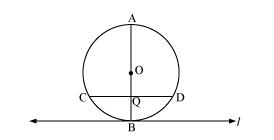
Solution 9



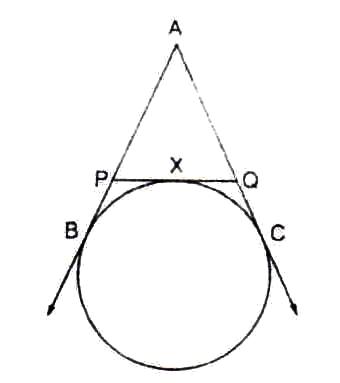
Solution 10

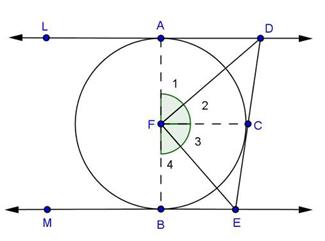
Solution 11



Solution 12

Solution 13

Solution 14

Solution 15



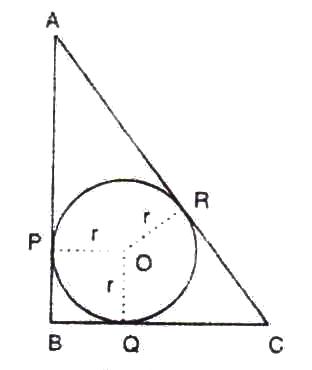
Solution 16

Solution 17

Solution 18

Solution 19

Solution 20

 

 

 

 

 

 

 

 

 

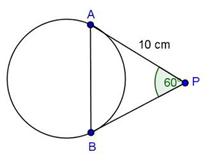
Solution 21


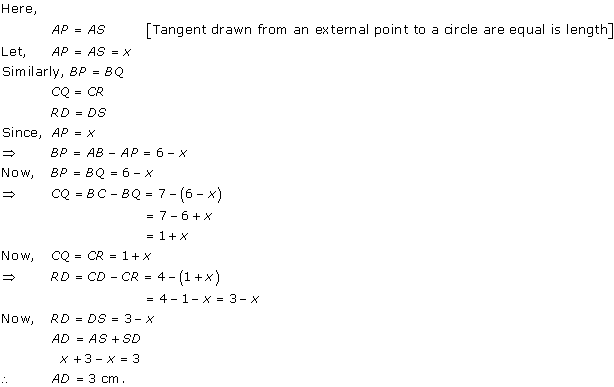
Solution 22

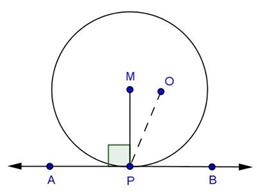
Solution 23



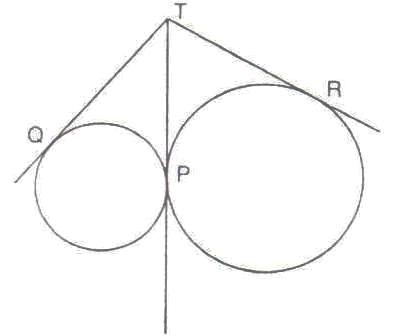
Solution 24

 

 

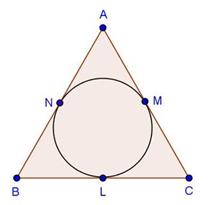
AP = AQ , BP = PR and CR = CQ (tangents from an external point)

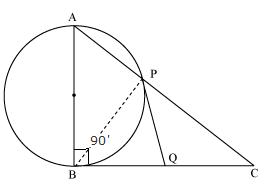
Perimeter of ∆ABC = AB + BR + RC + CA

= AB + BP + CQ + CA

= AP + AQ

= 2AP

∆APO is a right-angled triangle. AO2 = AP2 + PO2

132 = AP2 + 52

AP2 = 144

AP = 12

∴ Perimeter of ∆ABC = 24 cm

Solution 25

Solution 26

Solution 27

Solution 28

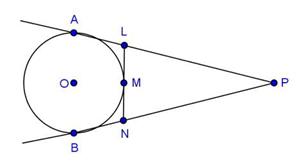
Solution 29

Solution 30

 

 



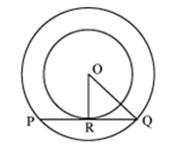
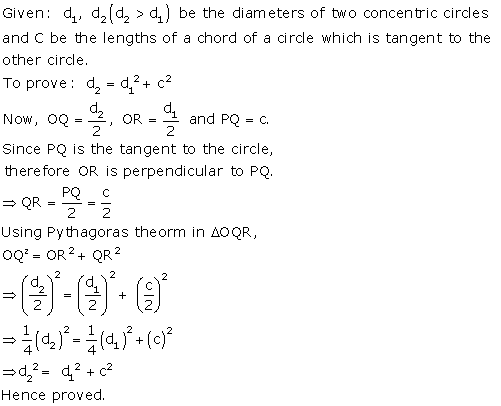
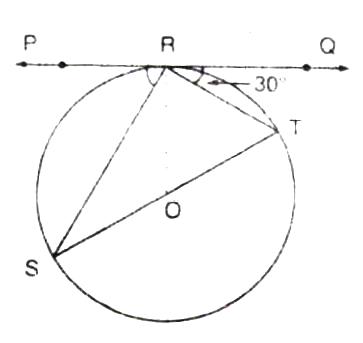
Solution 31

Since RS is drawn parallel to the tangent PQ,

∠SRQ = ∠PQR

Also, PQ = PR

⇒ ∠PQR = ∠PRQ

In ∆PQR,

∠PQR + ∠PRQ + ∠QPR = 180°

⇒∠PQR + ∠PQR + 30° = 180°

⇒2∠PQR = 150°

⇒∠PQR = 75°

⇒∠SRQ =∠PQR = 75° (alternate angles)

Also, ∠RSQ =∠RQP = 75° (the angle between a tangent and a chord through the point of contact is equal to an angle in the alternate segment.)

In ∆RSQ,

∠RSQ + ∠SRQ + ∠RQS = 180°

⇒75° + 75° + ∠RQS = 180°

⇒ ∠RQS =30° 

Solution 32

 

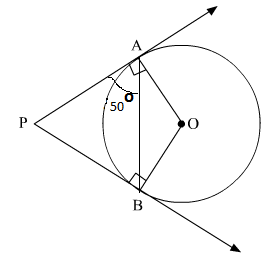
Solution 33

Solution 34

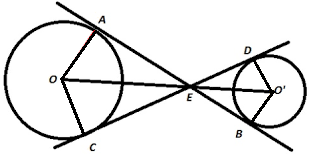
Solution 35

 

 

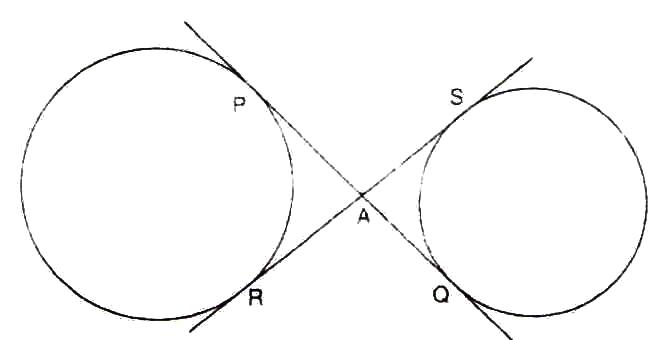
Solution 36



Solution 37

 

 

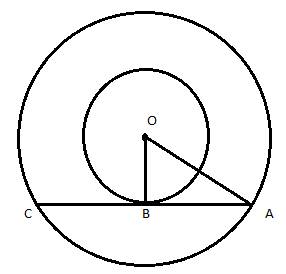
Since AC is the tangent to the circle with radius 9 cm, we have OB ⊥ AC.

Hence, by applying the Pythagoras Theorem, we have,

OA2 = OB2 + AB2

⇒ 152 = 92 + AB2

⇒ AB2 = 152 - 92

⇒ AB2 = 225 - 81 = 144

∴ AB = 12 cm

We know that the perpendicular drawn from the centre of a circle to any chord of the circle bisects the chord.

Here, OB is the perpendicular and AC is the length of the chord of the circle with radius 15 cm.

So,

AC = 2 × AB = 2 × 12 = 24 cm

 

Length of the chord of the larger circle which touches the smaller circle = 24 cm.

Solution 38

 

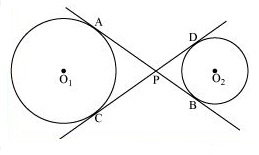
Solution 39

 

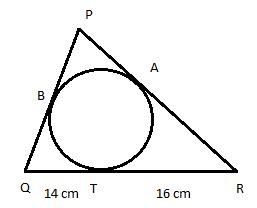
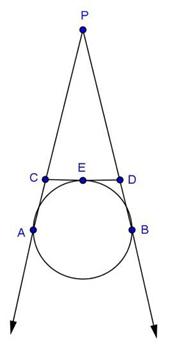
Let PA = PB = x

Tangents drawn from an external point are equal in length. QB = QT = 14 cm , RA = RT = 16 cm

 

PR = (x + 16) cm, PQ = (x + 14)cm,

QR = 30 cm

 

= x + 30

 

Area of ∆PQR

 

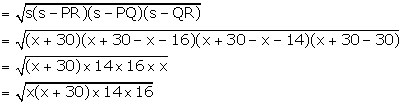
Area of ∆PQR = 336 cm2

 

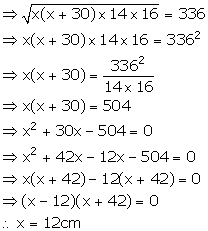
Side PR = (12 + 16) = 28 cm

Side PQ = (12 + 14) = 26 cm

Solution 40

Solution 41

 

 

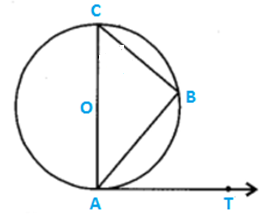
Solution 42

Let M and N be the points where AB and AC touch the circle respectively.

 

 

 

 

 

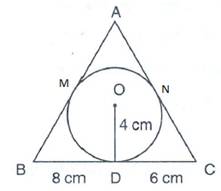
Tangents drawn from an external point to a circle are equal

⇒ AM=AN

BD=BM=8 cm and DC=NC=6 cm

 

 

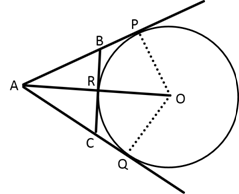
Solution 43

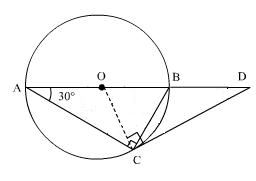
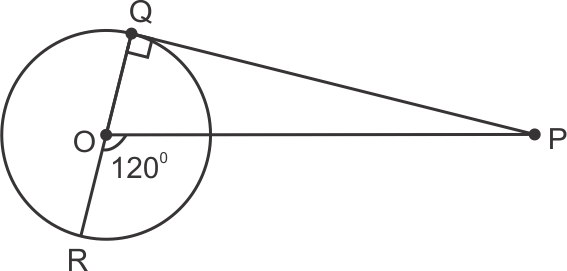
∠AOQ=58° (given)

In right ∆BAT,

∠ABT + ∠BAT + ∠ATB=180°

29° + 90° + ∠ATB=180° 

∠ATB = 61° 

that is, ∠ATQ = 61° 

Solution 44

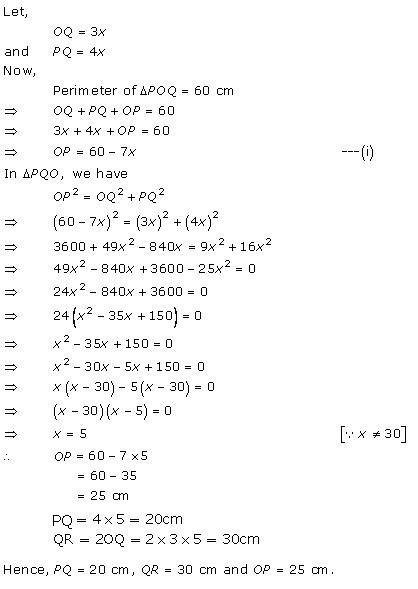
Solution 45

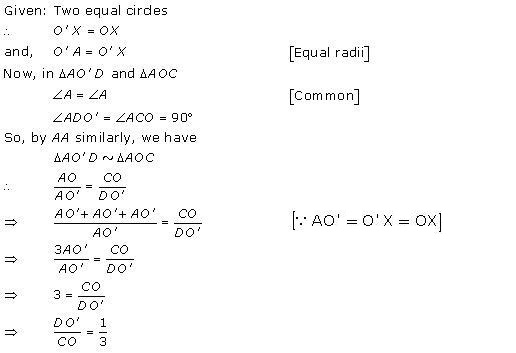
Solution 46

In ∆AOP,

OA = OP (radii) ∆AOP is an isosceles triangle. OE is a median.

In an isosceles triangle,the median drawn∴∠OEA = 90o

In ∆AOE and ∆ABC,

∠ABC = ∠OEA = 90o

∠A is common.

∆AEO ~ ∆ABC…(AA test)

Solution 47

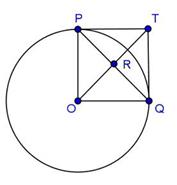
Solution 48

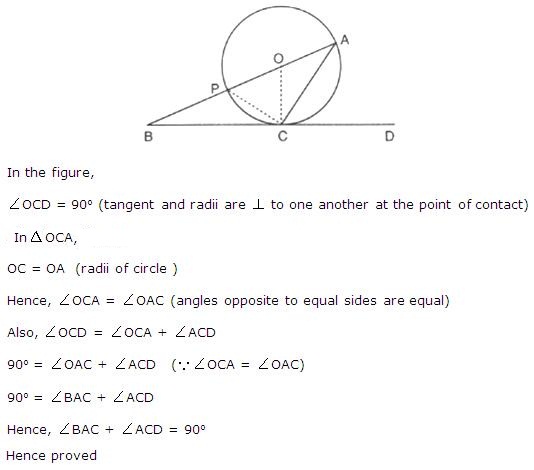
Solution 49

 

 

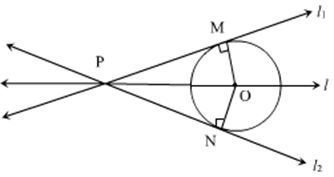
Solution 50

PR = PQ…(tangents fromexternal points)

PQ = 5 cm

Also,

OQ is perpendicular to PS …(tangent is perpendicular to the radius)

Now, in a circle,a perpendicular drawn from the centre of a circle bisects the chord.

So, OQ bisects PS.

PQ = QS

QS = 5 cm

PS = 10 cm

Solution 51

In DPQR,

∠POR is an external angle.

So,

∠POR = ∠PQO + ∠OPQ

Now, PQ is tangent to the circle with radius OQ.

∠PQO = 90o

130˚ = 90˚ + ∠OPQ

∠OPQ = 40o

∠1 = 40o

Now,

Minor arc RT subtends a 130˚ angle at the centre.

So, it will subtend a 65˚angle at any other point on the circle.∠RST = 65˚

∠2 = 65˚

∠1 + ∠2 =105˚

Solution 52

AP = PB = 12 cm, AC = CQ = 3 cm and QD = DB = 3 cm …(tangent from external point)

PA = 12 cm, PC + CA = 12

PC + 3 = 12

PC= 9 …(i)

Now,

PB = 12

PD + DB = 12

PD + 3 = 12

PD = 9 …(ii)

PC + PD = 18 cm…from (i) and (ii)

Circles Exercise 8.48

Solution 1

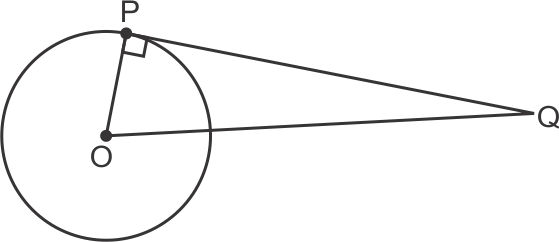
radius = 5 cm

So, OP = 5 cm

OQ = 12 cm

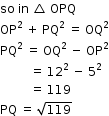
begin mathsize 12px style so space in space triangle space OPQ OP squared space plus space PQ squared space equals space OQ squared PQ squared space equals space OQ squared space minus space OP squared space space space space space space space space space space equals space 12 squared space minus space 5 squared space space space space space space space space space space equals space 119 PQ space equals space square root of 119 end style

So, the correct option is (d).

Solution 2

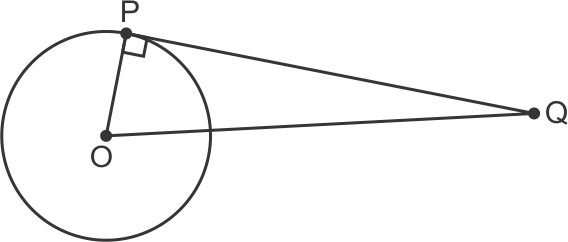
PQ is a tangent to the circle

So, OP2 + PQ2 = OQ2

OP2 = OQ2 - PQ2

      = (25)2 - (24)2

      = 49

OP = 7

So, the correct option is (a).

Solution 3

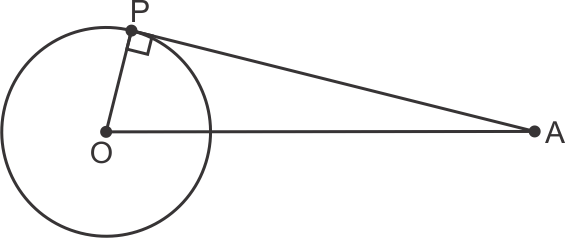
Given OP = 3 cm

         PA = 4 cm

Hence, OA2 = OP2 + PA2

OA2 = 32 + 42

      = 25

OA = 5 cm

So, the correct option is (c).

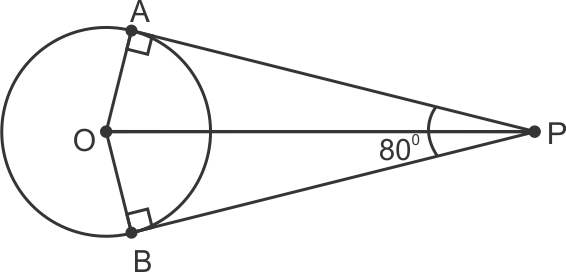
Solution 4

begin mathsize 12px style We space know space tangents space from space same space point space to space circle space are space inclined space at space same space angle. Hnece space angle APO space equals space angle BPO space space space space space space space space space space space space space angle APO space equals space 1 half angle straight P space space space space space space space space space space space space space space angle APO space equals space 40 degree In space triangle OAP angle straight A space plus space angle POA space plus space angle APO space equals space 180 degree space space space space space space space space space space space space space angle POA space equals space 180 degree space minus space 90 degree space minus space 40 degree space space space space space space space space space space space space space space space space space space space space space space space space space space space equals space 50 degree So comma space the space correct space option space is space left parenthesis straight a right parenthesis. end style

Circles Exercise 8.49

Solution 5

begin mathsize 12px style PTQO space is space straight a space quadrilateral space sum space of space all space angles space equals space 360 degree angle straight P space plus space angle straight Q space plus space angle POQ space plus space angle PTQ space equals space 360 degree 90 degree space plus space 90 degree space plus space 110 degree space plus space angle PTQ space equals space 360 degree angle PTQ space plus space 290 degree space equals space 360 degree angle PTQ space equals space 70 degree So comma space the space correct space option space is space left parenthesis straight b right parenthesis. end style

Solution 6

begin mathsize 12px style triangle OPQ space is space an space isoceles space triangle so comma space OP space equals space PQ and space angle straight P space equals space 90 degree and space angle straight O space equals space angle straight Q also space angle straight P space plus space angle straight O space plus space angle straight Q space equals space 180 degree 2 angle straight Q space equals space 180 degree space minus space 90 degree angle straight Q space equals space 45 degree So comma space the space correct space option space is space left parenthesis straight b right parenthesis. end style

Solution 7

begin mathsize 12px style AO subscript 1 space equals space straight O subscript 1 straight C space and space straight O subscript 2 straight B space equals space CO subscript 2 so space angle CBO subscript 2 space equals space angle BCO subscript 2 space equals space 45 degree space space space space.... open parentheses 1 close parentheses and space angle CAO subscript 1 space equals space angle straight O subscript 1 CA space equals space 45 degree space space space.... open parentheses 2 close parentheses also space angle straight O subscript 1 CO subscript 2 space equals space 180 degree space space space space space space space space space space space..... open parentheses 3 close parentheses so space from space open parentheses 1 close parentheses comma space open parentheses 2 close parentheses comma space open parentheses 3 close parentheses angle straight O subscript 1 CA space plus space angle straight O subscript 2 CB space plus space angle ACB space equals space 180 degree 45 degree space plus space 45 degree space plus space angle ACB space equals space 180 degree angle ACB space equals space 90 degree So comma space the space correct space option space is space left parenthesis straight d right parenthesis. end style

Solution 8

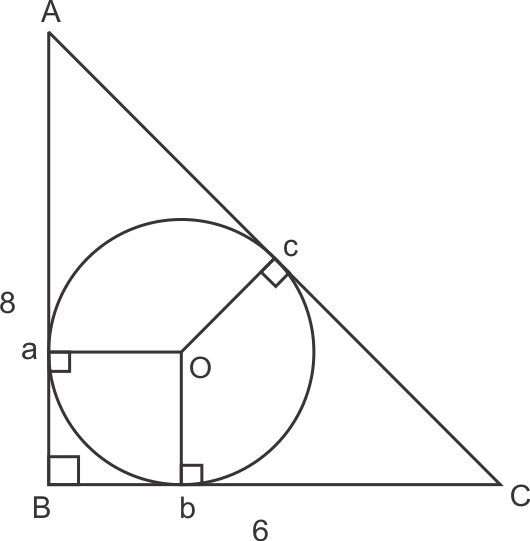
Tangents from same point to circle have equal length.

Hence Bb = Ba

          bC = Cc

          Ac = Aa

Let Ba = x    then Bb = x

bc = 6 - x     and Aa = 8 - x

and Cc = 6 - x and Ac = 8 - x

So AC = AC + cC

         = 6 - x + 8 - x

AC = 14 - 2x       ......(1)

Also AC2 = AB2 + BC2

             = 82 + 62 

             = 100

AC = 10    .....(2)

from (1) & (2)

14 - 2x = 10

4 = 2x

x = 2           also aB = Ob = radius = 2 cm

So, the correct option is (b).

Solution 9

begin mathsize 12px style angle POR space equals space 120 degree so space angle POQ space equals space 180 degree space minus space angle POR space space space space space space space space space space space space space space space space space space space space equals space 60 degree angle OPQ space plus space angle straight Q space plus space angle POQ space equals space 180 degree angle OPQ space plus space 90 degree space plus space 60 degree space equals space 180 degree angle OPQ space equals space 30 degree So comma space the space correct space option space is space left parenthesis straight c right parenthesis. end style

Solution 10

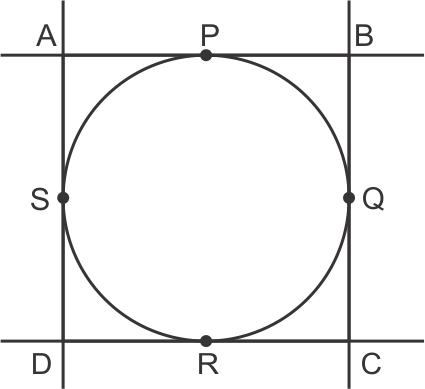
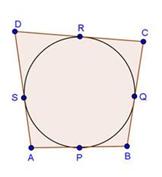
Tangents from same point are of equal length.

AP = AS, PB = BQ

QC = CR, RD = DS

AB = AP + PB      .....(1)

BC = BQ + QC   ......(2)

CD = CR + RD   .....(3)

AD = AS + DS .....(4)

Adding (1) & (3)

AB + CD = AP + BP + CR + RD

            = AS + BQ + CQ + DS

            = (AS + DS) + (BQ + CQ)

from (2) & (4)

AB + CD = AD + BC

So, the correct option is (b).

Solution 11

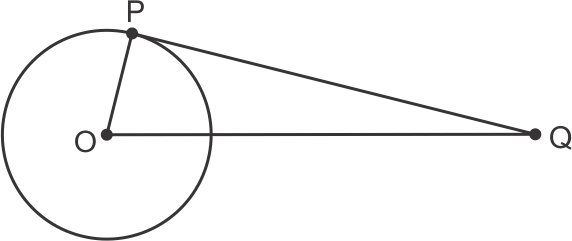
Given OQ = 8 cm

         OP = 6 cm

OP2 + PQ2 = OQ2

62 + PQ2 = 82

       PQ2 = 64 - 36

             = 28

PQ = begin mathsize 12px style 2 square root of 7 end style

So, the correct option is (b).

Solution 12

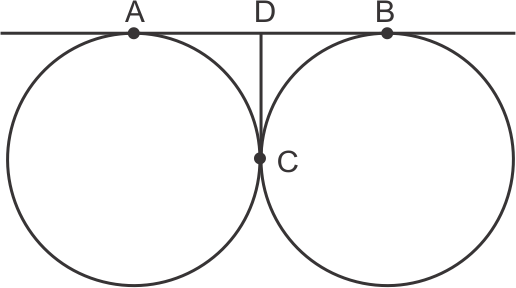
DA and DC are tangents to circle from same point

so, DA = DC ......(1)

similarly DB = DC   ......(2)

(1) + (2)

2DC = DA + DB

2DC = AB

AB = 2 × 4

     = 8 cm

So, the correct option is (c).

Solution 13

AD = AE        .......(1)

CD = CF    ......(2)

BF = BE   .....(3)

from (1)

2AD = 2AE

       = AE + AD

       = (AB + BE) + (AC + CD)

       = AB + BF + AC + CF

       = AB + AC + BC

So, the correct option is (b).

Solution 14

begin mathsize 12px style SQ space is space diameter and space SQ space equals space 6 space cm so space OQ space equals space SQ over 2 space equals space 3 space cm and space QR equals space 4 space cm OR squared space equals space OQ squared space plus space QR squared space space space space space space space space space space equals space 4 squared space plus space 3 squared space space space space space space space space space space equals space 25 OR space equals space 5 space cm So comma space the space correct space option space is space left parenthesis straight d right parenthesis. end style

Circles Exercise 8.50

Solution 15

begin mathsize 12px style AQ space equals space 4 space cm space space PC space equals space 5 space cm space space BR space equals space 6 space cm space space AQ space and space AR space are space tangent space to space circle space from space same space point. space space Hence space AQ space equals space AR space equals space 4 space cm space space space..... left parenthesis 1 right parenthesis space space similarly space space BR space equals space BP space equals space 6 space cm space space space space space..... left parenthesis 2 right parenthesis space space and space PC space equals space CQ space equals space 5 space cm space space space space...... left parenthesis 3 right parenthesis space space perimeter space of space triangle ABC space equals space AB space plus space BC space plus space CA space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space equals space left parenthesis AR space plus space RB right parenthesis space plus space left parenthesis BP space plus space PC right parenthesis space plus space open parentheses CQ space plus space QA close parentheses space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space equals space open parentheses AQ space plus space AR close parentheses space plus space open parentheses RB space plus space BP close parentheses space plus space open parentheses CP space plus space CQ close parentheses space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space equals space open parentheses 4 space plus space 4 close parentheses space plus space open parentheses 6 space plus space 6 close parentheses space plus space open parentheses 5 space plus space 5 close parentheses space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space equals space 8 space plus space 12 space plus space 10 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space equals space 30 space cm So comma space the space correct space option space is space left parenthesis straight a right parenthesis. end style

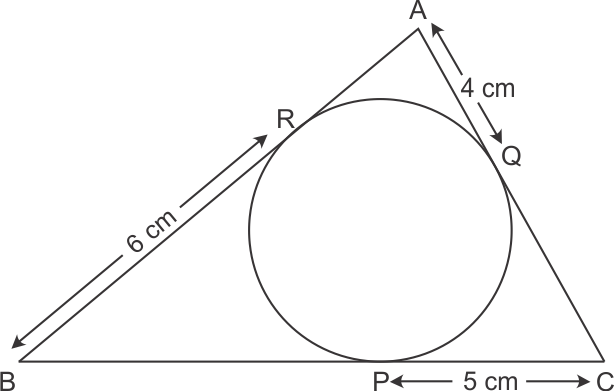
Solution 16

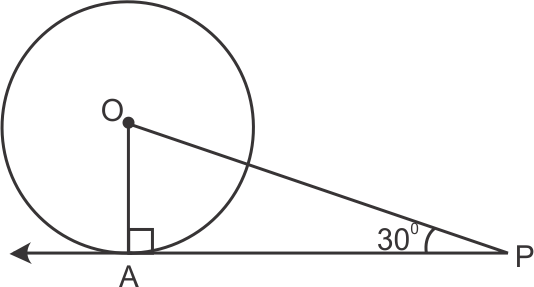
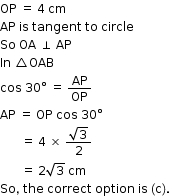
begin mathsize 12px style OP space equals space 4 space cm AP space is space tangent space to space circle So space OA space perpendicular space AP In space triangle OAB cos space 30 degree space equals space AP over OP AP space equals space OP space cos space 30 degree space space space space space space space equals space 4 space cross times space fraction numerator square root of 3 over denominator 2 end fraction space space space space space space space equals space 2 square root of 3 space cm So comma space the space correct space option space is space left parenthesis straight c right parenthesis. end style

Solution 17

AP = PQ    ....(1)

and OA2 = OP2  + PA2

      (15)2 = (9)2 + AP2

       AP2 = 225 - 81

             = 144

       AP = 12

AP + AQ = 2AP

             = 24 cm

So, the correct option is (c).

Solution 18

begin mathsize 12px style radius space equals space 5 space cm OP space perpendicular space XY space and space XY space parallel to space AB so space OQ space perpendicular space AB and space PE space equals space 8 space cm also space AB space equals space AE space plus space EB space space space space space space space space space space space space space space space space equals space 2 AE space space space space space space space space space space space space space space space space space space open curly brackets AE space equals space EB close curly brackets PE space equals space 8 space cm OP space equals space 5 space cm OE space equals space 3 space cm space and space OA space equals space 5 space cm OA squared space equals space OE squared space plus space AE squared AE squared space equals space 5 squared space minus space 3 squared space space space space rightwards double arrow space AE space equals space 4 space cm Hence space AB space equals space 8 space cm So comma space the space correct space option space is space left parenthesis straight d right parenthesis. end style

Solution 19

begin mathsize 12px style In space triangle OPT angle POT space plus space angle OPT space plus space angle straight T space equals space 180 degree angle POT space plus space angle OPT space equals space 180 degree space minus space angle straight T space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space equals space 180 degree space minus space 90 degree space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space equals space 90 degree So comma space the space correct space option space is space left parenthesis straight c right parenthesis. end style

Circles Exercise 8.51

Solution 20

AB = 12 cm

BC = 8 cm

AC = 10 cm

Let AD = x  

      AF = x

     BD = 12 - x

and BE = BD = 12 - x

CE = BC - BE

     = 8 - (12 - x)

     = x - 4

and CE = CF = x - 4

AC = AF + FC

     = x + x - 4

AC = 2x - 4

Given, AC = 10 cm

so 2x - 4 = 10

2x = 14

x = 7 cm

AD = 7 cm

So, the correct option is (d).

Solution 21

AP = BP     given

and AP = AQ

also BP = BR

from this, we conclude that

AQ = BR     .....(1)

We know CR = CQ    .....(2)

from (1) & (2)

AQ + CR = BR + CR

AQ + CQ = BR + CR

AC = BC

So, the correct option is (b).

Solution 22

AP = 10 cm

AO = 6 cm

OB = 3 cm

AP2 + OA2 = OP2

OP2 = 102 + 62

OP2 = 136

Also OB2 + BP2 = OP2 

        32 + BP2 = 136

        BP2 = 136 - 9

        begin mathsize 12px style BP space equals space square root of 127 end style

So, the correct option is (b).

Solution 23

begin mathsize 12px style angle RPO space equals space 90 degree given space angle RPQ space equals space 60 degree so space angle QPO space equals space angle RPO space minus space angle RPQ space space space space space space space space space space space space space space space space space space space space space equals space 90 degree space minus space 60 degree space space space space space space space space space space space space space space space space space space space space space equals space 30 degree In space triangle OPQ comma space OP comma space is space equal space to space OQ Hence space angle OPQ space equals space angle OQP... left parenthesis since space OP space equals space OQ space which space are space radii space of space the space same space circle right parenthesis space space space space space space space space space space space space space angle OPQ space equals space angle OQP space equals space 30 degree In space triangle OPQ angle straight O space plus space angle OPQ space plus space angle OQP space equals space 180 degree angle POQ space equals space 180 degree space minus space 30 degree space minus space 30 degree space space space space space space space space space space space space space space space equals space 120 degree So comma space the space correct space option space is space left parenthesis straight c right parenthesis. end style

Circles Exercise 8.52

Solution 24

PA = PD

AQ = QB

and PQ = PA + AQ

PQ = PD + QB

Hence PD + QB = PQ

So, the correct option is (a).

Solution 25

PQ = PT     .....(1)

and PT = PR     .....(2)

so from (1) & (2)

PQ = PR

PQ = PR = 4.5 cm

QR = PQ + PR

     = 4.5 + 4.5 = 9 cm

So, the correct option is (a).

Solution 26

begin mathsize 12px style APB space is space tangent so space OP space perpendicular space APB Hence space angle OPB space equals space 90 degree angle OPQ space equals space 90 degree space minus space 50 degree space space space space space space space space space space space space space space space equals space 40 degree In space triangle OPQ OP space equals space OQ Hence space angle OPQ space equals space angle OQP space equals space 40 degree so space angle POQ space equals space 180 degree space minus space angle OPQ space minus space angle OQP space space space space space space space space space space space space space space space space space space space space space equals space 180 degree space minus space 40 degree space minus space 40 degree space space space space space space space space space space space space space space space space space space space space space equals space 100 degree So comma space the space correct space option space is space left parenthesis straight a right parenthesis. end style

Solution 27

begin mathsize 12px style AC space parallel to space PB and space PA space equals space PB In space triangle PAB comma angle PAB space equals space angle PBA angle PAB space plus space angle PBA space plus space angle APB space equals space 180 degree angle PAB space equals space 75 degree AC space parallel to space BP By space alternative space interior space angle space property angle CAB space equals space angle ABP space equals space 75 degree OB space perpendicular space BP comma Hence space angle OBA space equals space angle OBP space minus space angle ABP space space space space space space space space space space space space space space space angle OBA space equals space angle OAB space equals space 15 degree so space angle AOB space equals space 180 degree space minus space angle OAB space minus space angle OBA space equals space 150 degree We space also space know space that space the space angle space made space by space any space chord space at space the space centre space is space twice space the space angle space made space by space same space chord space on space the space space circle. Hence space angle AOB space equals space 2 angle ACB space space space space space space space space space space space space space space space angle ACB space equals space 1 half cross times 150 degree space space space space space space space space space space space space space space space space space space space space space space space space space space space space equals space 75 degree In space triangle ABC comma space angle ACB space equals space 75 degree space and space angle CAB space equals space 75 degree angle ABC space equals space 180 degree space minus space angle ACB space minus space angle CAB space space space space space space space space space space space space space equals space 30 degree So comma space the space correct space option space is space left parenthesis straight c right parenthesis. end style

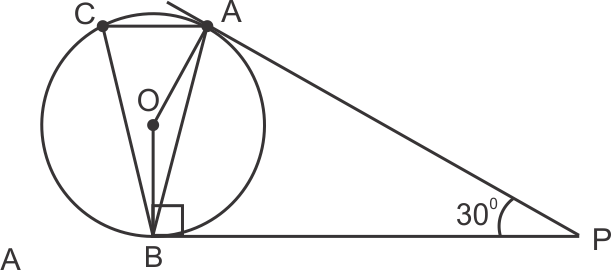
Circles Exercise 8.53

Solution 28

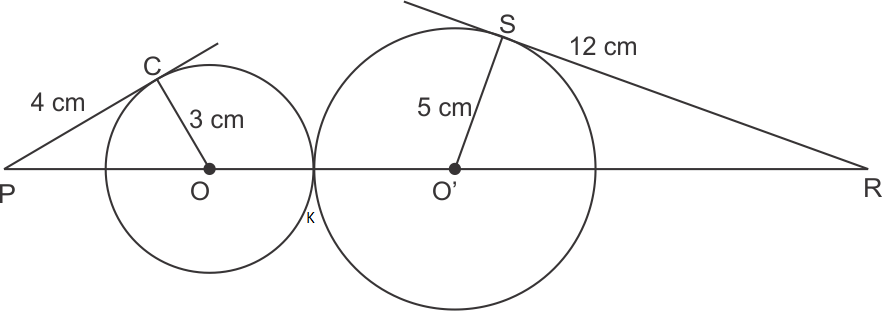
radius of circle 1 = 3 cm

radius of circle 2 = 5  cm

OP2 = OQ2 + QP2         and    O'S2 + SR2 = O'R2 

OP2 = 42 + 32                         O'R2 = 52 + 122     

      = 16 + 9                          O'R2 = 169                       

      = 25                                O'R' = 13 cm

OP = 5 cm

OO' = OK + KO'

       = 3 + 5

       = 8 cm

PR = PO + OK + KO' + O'R

     = 5 + 3 + 5 + 13

     = 26 cm

So, the correct option is (b).

Solution 29

begin mathsize 12px style AO space equals space AO apostrophe space plus space straight O apostrophe straight P space plus space PO space space space space space space space space equals space straight r space plus space straight r space plus space straight r space space space space space space space space equals space 3 straight r AO apostrophe space equals space straight r AO space colon space AO apostrophe space equals space fraction numerator 3 straight r over denominator straight r end fraction space equals space 3 space So comma space the space correct space option space is space left parenthesis straight c right parenthesis. end style

Solution 30

OB = OC = OA = 5 cm

OQ = OP = 3 cm

OB2 = OQ2 + BQ2

BQ2 = OB2 - OQ2

      = 52 - 32

      = 16

BQ = 4 cm

also BQ = BP

BP = 4 cm

In ΔOPC,

OP2 + PC2 = OC2

PC2  = OC2 - OP2

       = 52 - 32

       = 16

PC = 4 cm

BC = BP + PC = 4 + 4 = 8 cm

So, the correct option is (c).

Solution 31

Given PR = 7.5 cm

so PR = PQ

PQ = 7.5 cm

PS is the chord to the larger circle. We know that, perpendicular drawn from centre bisect the chords.

Hence PQ = QS

PS = PQ + QS

     = 2PQ

     = 2 × 7.5

     = 15 cm

So, the correct option is (c).

Circles Exercise 8.54

Solution 32

AC = AB      .....(1)

BD = DP     ......(2)

PE = EC    ......(3)

AB = 8 so AC = 8 cm

PE = 3 so EC = 3 cm

AE = AC - EC = 8 - 3 = 5 cm

So, the correct option is (c).

Solution 33

begin mathsize 12px style In space triangle space OPQ angle OQP space equals space 90 degree angle OPQ space equals space 35 degree also comma space angle OQP space plus space angle OPQ space plus space straight b space equals space 180 degree straight b space equals space 180 degree space minus space 90 degree space minus space 35 degree space space space space equals space 55 degree We space also space know comma space that space if space two space tangent space are space drawn space from space same space point space to space circle comma space touches space at space straight Q comma space straight R space then space angle QPR space is space bisected space by space OP. Hence space angle OPQ space equals space angle OPR space space space space space space space space space space space space space space space space space space space space 35 degree space equals space straight a straight a space equals space 35 degree space and space straight b space equals space 55 degree So comma space the space correct space option space is space left parenthesis straight b right parenthesis. end style

Solution 34

begin mathsize 12px style angle OQT space equals space 90 degree space as space OQ space perpendicular space to space TQ given space angle PQT space equals space 60 degree Hence space angle OQP space equals space angle OQT space minus space angle PQT space space space space space space space space space space space space space space space space space space space space space space space space space space equals space 30 degree increment OQP space is space isoceles space with space OP space equals space OQ Hence comma space angle OQP space equals space angle OPQ space equals space 30 degree So comma space the space correct space option space is space left parenthesis straight b right parenthesis. end style

Circles Exercise 8.55

Solution 35

PA = AR

AR = 4 cm

BP = BQ and QC = RC

BQ = 3 cm

Given AC = 11

AR + RC = 11

4 + RC = 11

RC = 7

so QC = 7 cm

BC = BQ + QC

     = 3 + 7

     = 10 cm

So, the correct option is (b).

Solution 36

EK = 9 cm

and EK = EM

Hence EM = 9 cm         .....(1)

Also EK = ED + DK

and DK = DH

EK = ED + HD     .......(2)

EM = EF + FM

and FM = FH

EM = EF + FH       ......(3)

(2) + (3)

EK + EM = ED + EF + DH + HF

18 = ED + DF + EF

perimeter = 18 cm

So, the correct option is (a).

Solution 37

begin mathsize 12px style DE space equals space DF space equals space 5 space cm We space know space AD space bisects space the space angle space EDF space since space straight D space is space the space intersection space of space the space two space tangents space and space AD space is space the space line space segment space joining space the centre space to space the space point space of space intersection space of space the space two space tangents. rightwards double arrow angle EDA space equals space 45 degree Hence space in space triangle AED comma AE space is space radius space of space circle Also space tan 45 degree space equals space AE over ED AE space equals space ED space tan 45 degree space space space space space space equals space ED space space space space space space equals space 5 space cm space So comma space the space correct space option space is space left parenthesis straight b right parenthesis. end style

Circles Exercise 8.56

Solution 38

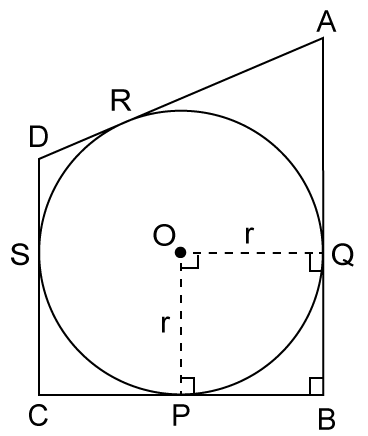
AB = 29 cm

AD = 23

DS = 5 cm

DS = DR

so DR = 5 cm

AR = AD - DR

     = 23 - 5

     = 18 cm

AR = AQ 

AQ = 18 cm

BQ = AB - AQ

     = 29 - 18

BQ = 11 cm

As OP || BQ and OQ || PB 

Hence, OP = BQ

OP = 11 cm

So, the correct option is (a).

Solution 39

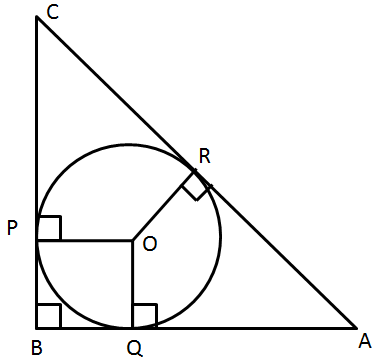
AB = 5 cm

BC = 12 cm

AB2  + BC2 = AC2

AC2 = 52 + 122

      = 169

AC = 13 cm

Let BQ = x

AQ = AR = 5 - x

CR = AC - AR

      = 13 - (5 - x)

      = x + 8

And CP = CR = x + 8

so BP = BC - PC

         = 12 - (x + 8)

         = 4 - x

But BP = BQ = x

4 - x = x

x = 2

and BQ || OP and OQ || PB

so BQ = PO

PO = 2 cm

So, the correct option is (c).

Solution 40

begin mathsize 12px style Let space angle OPA space equals space straight theta We space know space angle OPA space equals space angle OAP So comma angle AOP space equals space 180 degree space minus space open parentheses angle OPA space plus space angle OAP close parentheses angle AOP space equals space 180 degree space minus space 2 straight theta space space space space space.... open parentheses 1 close parentheses Let space angle straight O apostrophe PB space equals space straight alpha Hence space angle straight O apostrophe BP space equals space straight alpha So comma space angle BO apostrophe straight P space equals space 180 degree space minus space open parentheses angle straight O apostrophe PB space plus space angle straight O apostrophe BP close parentheses angle BO apostrophe straight P space equals space 180 degree space minus space 2 straight alpha space space space space space space space space.... open parentheses 2 close parentheses In space quadrilateral space ABO apostrophe straight O comma sum space of space all space angles space equals space 360 degree angle BAO space plus space angle ABO apostrophe space plus space angle AOO apostrophe space plus space angle BO apostrophe straight O space equals space 360 degree 90 degree space plus space 90 degree space plus space 180 space minus space 2 straight theta space plus space 180 space minus space 2 straight alpha space equals space 360 degree 540 degree space minus space 2 open parentheses straight alpha space plus space straight theta close parentheses straight alpha space plus space straight theta space equals space 90 degree space space space space... open parentheses 3 close parentheses Also space angle OPO apostrophe space equals space 180 degree angle APO space plus space angle APB space plus space angle BPO apostrophe space equals space 180 degree space straight theta plus space angle APB space plus straight alpha space space equals space 180 degree from space left parenthesis 3 right parenthesis space angle APB space equals space 180 degree space minus space 90 degree space space space space space space space space space space space space space space equals space 90 degree So comma space the space correct space option space is space left parenthesis straight d right parenthesis. end style

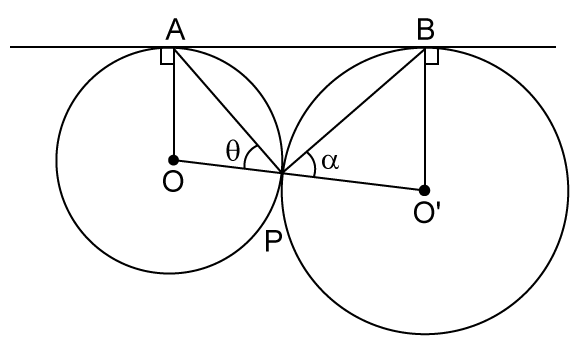
Solution 41

begin mathsize 12px style angle ORP space equals space angle OQP space equals space 90 degree Also space sum space of space all space angles space of space quadrilateral space PQOR space is space 360 degree angle ORP space plus space angle OQP space plus space angle QOR space plus space angle QPR space equals space 360 degree 90 degree space plus space 90 degree space plus space angle QOR space plus space 46 degree space equals space 360 degree angle QOR space equals space 360 degree space minus space open parentheses 180 degree space plus space 46 degree close parentheses angle QOR space equals space 134 degree So comma space the space correct space option space is space left parenthesis straight b right parenthesis. end style

Solution 42

PT = 3.8 cm

We know

PQ = PT and PT = PR

Hence PQ = 3.8 cm and PR = 3.8 cm

Now, QR = QP + PR

             = 3.8 + 3.8

QR = 7.6 cm

So, the correct option is (b).

Circles Exercise 8.57

Solution 43

AB = x cm

BC = 7 cm

CR = 3 cm

AS = 5 cm

CR = CQ

CQ = 3 cm

given BC = 7 cm

BQ = BC - QC

       = 7 - 3

       = 4 cm

And BQ = BP

so BP = 4 cm

Also AS = AP

Hence AP = 5 cm

AB = AP + BP

     = 5 + 4

     = 9 cm

x = 9 cm

So, the correct option is (b).

Solution 44

 

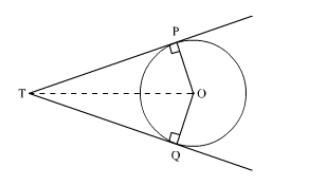
Solution 45

 

 

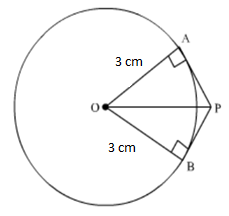
Solution 46

 

 

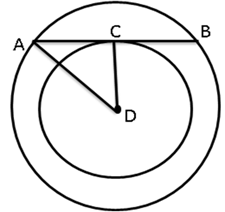
Solution 47

 

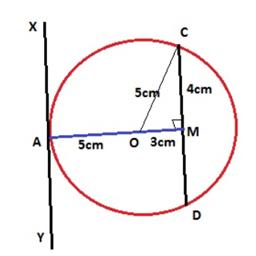
Solution 48

 

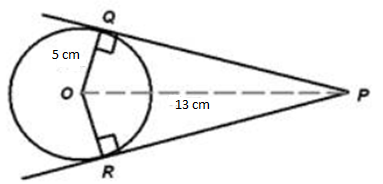
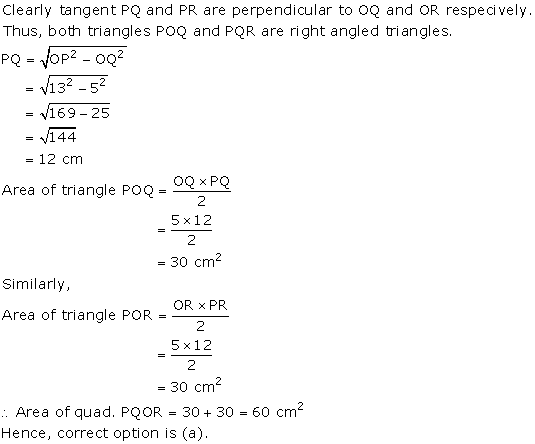
Solution 49

 

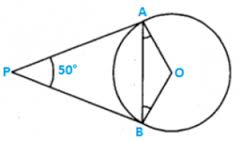
Solution 50

 

Circles Exercise 8.58

Solution 51

Solution 52