Chapter 1: Real Numbers
Class 10th R. D. Sharma Maths Solution
CBSE Class 10 Maths
R. D. Sharma Solution
Co-ordinate Geometry Exercise Ex. 6.1
Solution 1

Solution 2
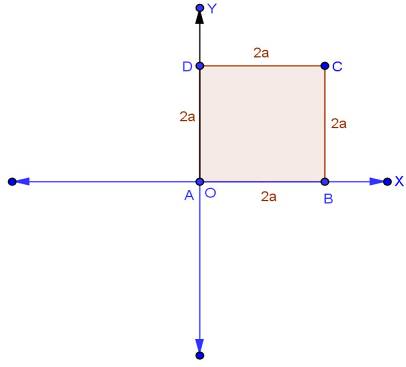
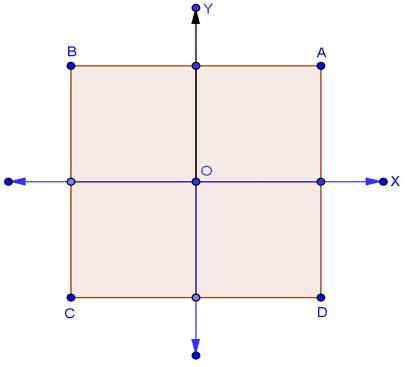

Solution 3
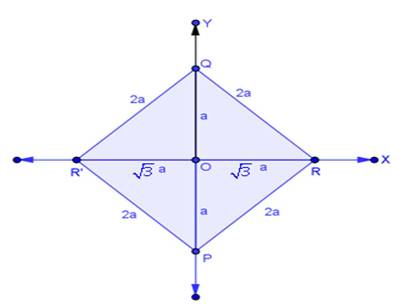

Co-ordinate Geometry Exercise Ex. 6.2
Solution 1 (i)

Solution 1 (ii)
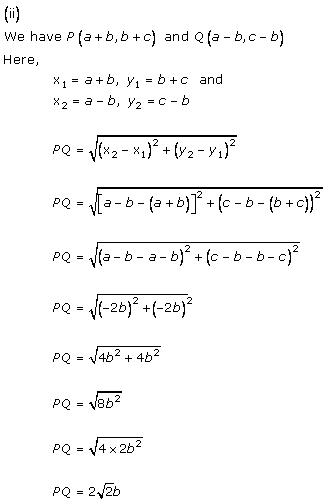
Solution 1 (iii)

Solution 1 (iv)

Solution 2

Solution 3

Solution 4

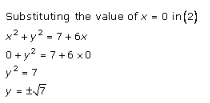
Solution 5

Solution 6
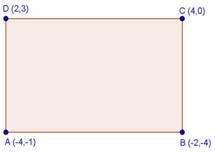
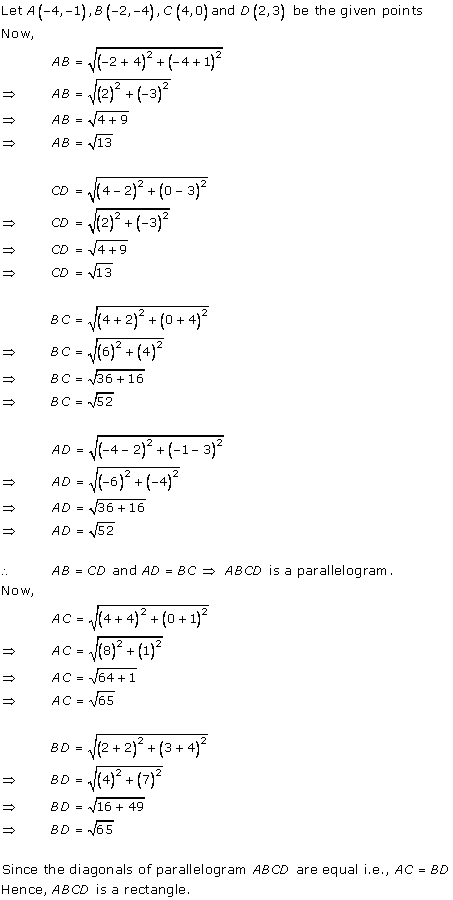
Solution 7
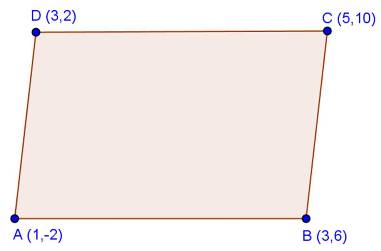
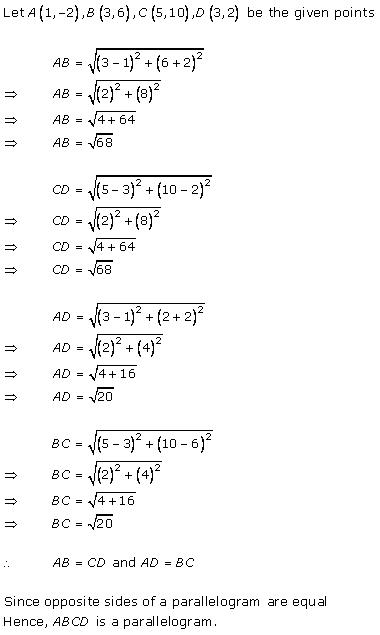
Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13

Solution 14
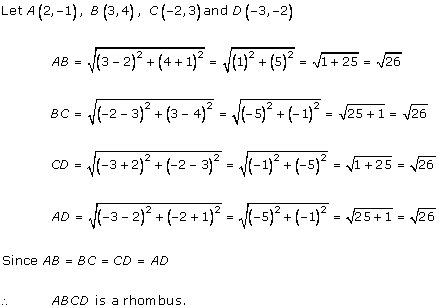
Solution 15

Solution 16
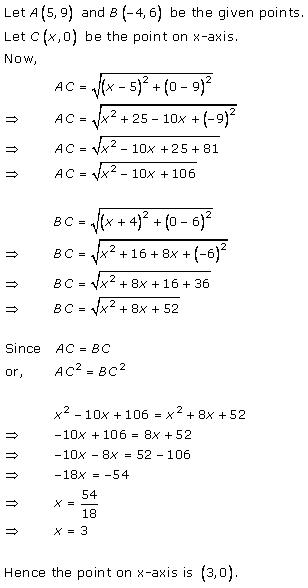
Solution 17

Solution 18
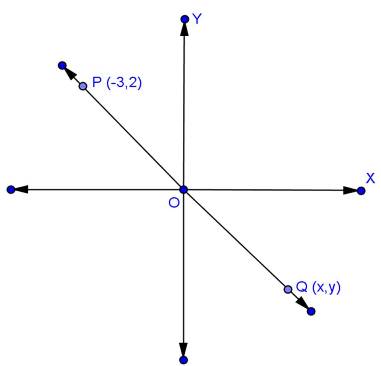

Solution 19
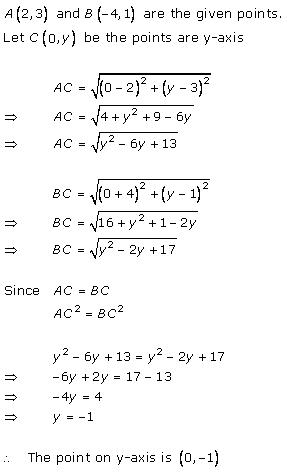
Solution 20


Solution 21

Solution 22
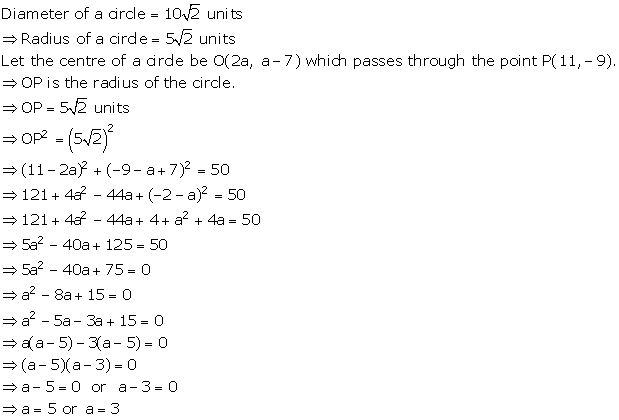
Solution 23

Solution 24

Solution 25

Solution 26
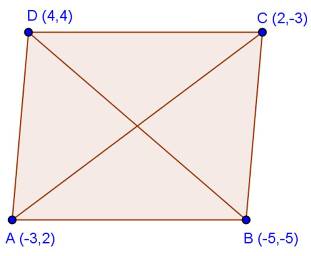


Solution 27
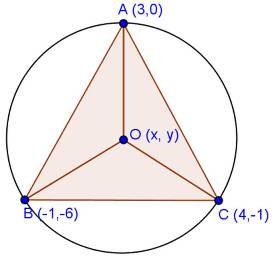

Solution 28

Solution 29(i)
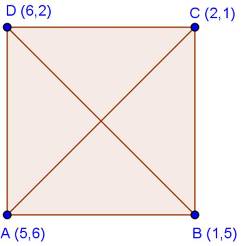
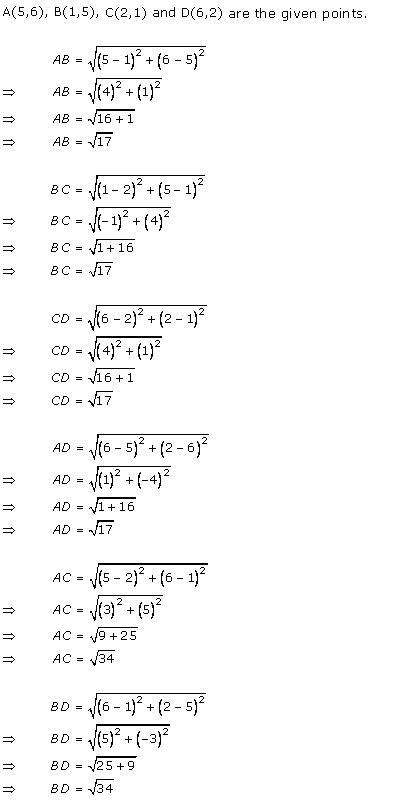

Solution 29(ii)
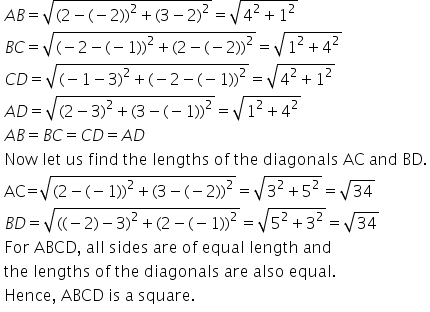
Solution 29(iii)
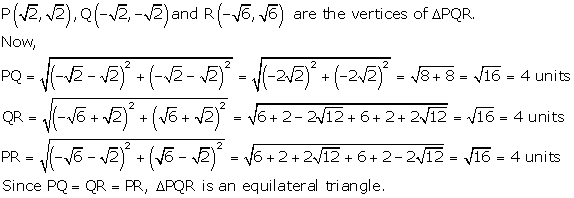
Solution 30

Solution 31

Solution 32

Solution 33
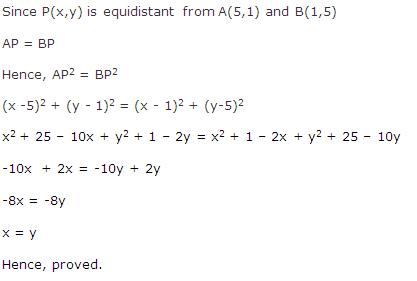
Solution 34
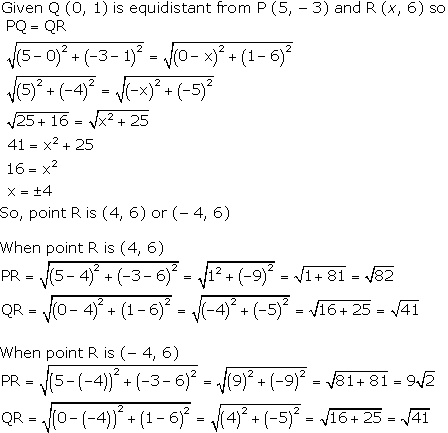
Solution 35
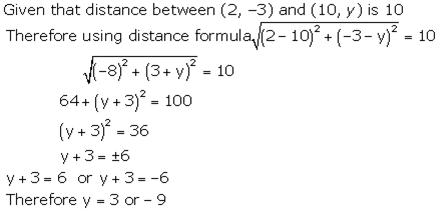
Solution 36
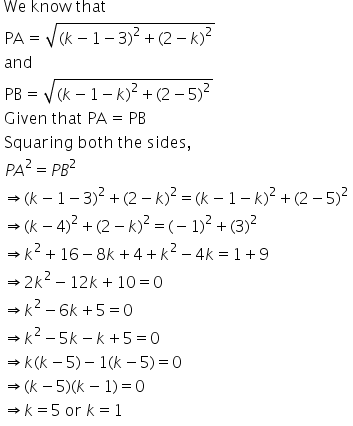
Solution 37

Solution 38
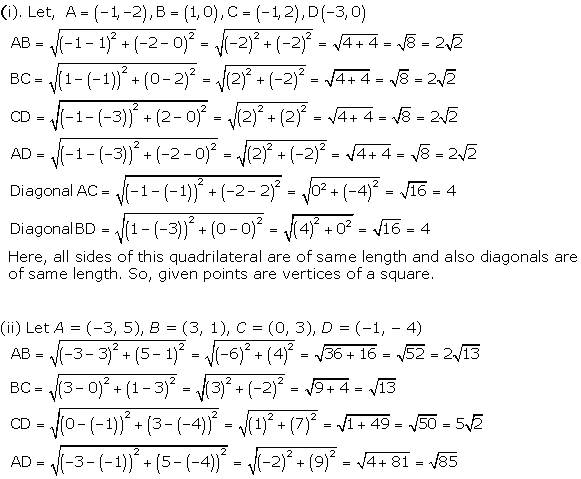

Solution 39

Solution 40

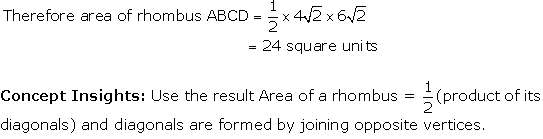
Solution 41

Solution 42

Solution 43
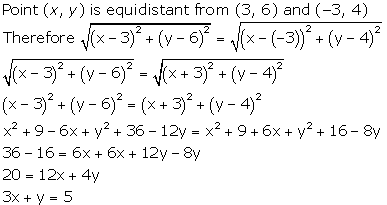
Solution 44
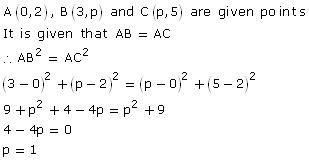
Solution 45
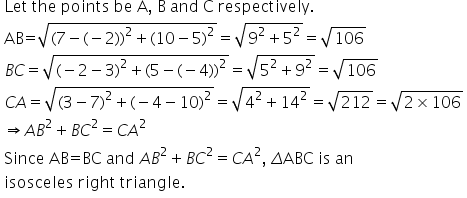
Solution 46
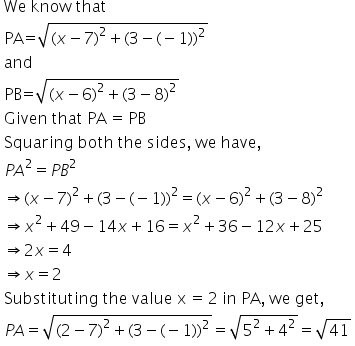
Solution 47

Solution 48
For an equilateral triangle, the perpendicular bisector of any side passes through the opposite vertex.
Both the points, (0, -3) and (0, 3), lie on the y-axis equidistant from the origin. Hence, the perpendicular bisector joining these two points is the x-axis.
Any point on the x-axis has the coordinates (a, 0).
The distance between (0, -3) and (0, 3) is 6.
Hence, the distance between (a, 0) and (0, 3) should also be 6.
62 = (a - 0)2 + (0 - 3)2
36 = a2 + 9
a2 = 27
![]()
![]()
Solution 49
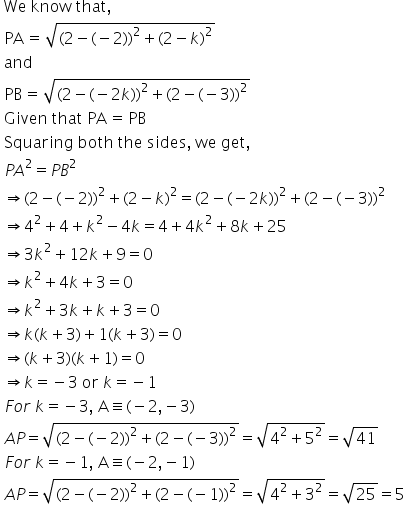
Solution 50
Using the distance formula,
AB=![]()
AC=![]()
BC=![]()
PQ=![]()
PR=![]()
QR=![]()
Now,
![]()
ΔABC ~ ΔPQR
by the SSS test.
Solution 51


Solution 52
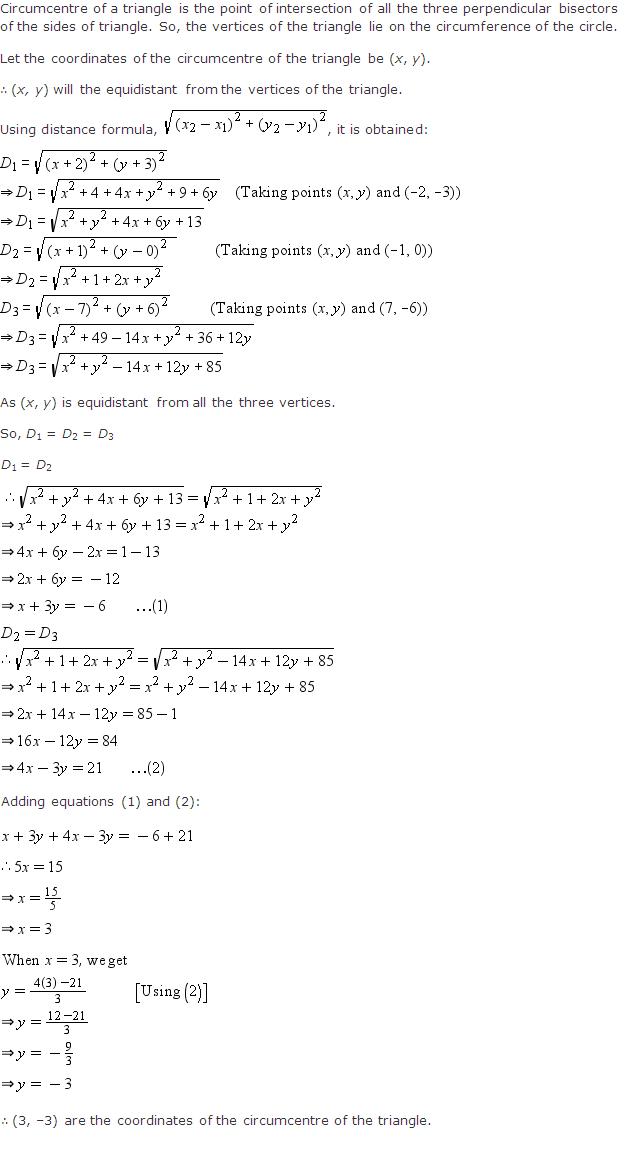
Solution 53
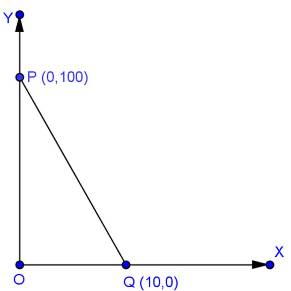

Solution 54

Solution 55


Solution 56
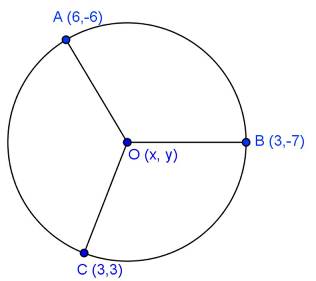

Solution 57
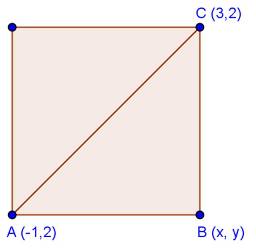

Co-ordinate Geometry Exercise Ex. 6.3
Solution 1
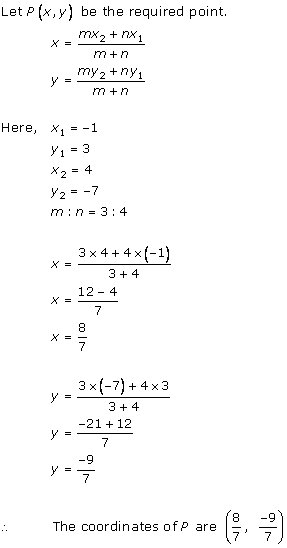
Solution 2
(i)

(ii)

(iii)

Solution 3
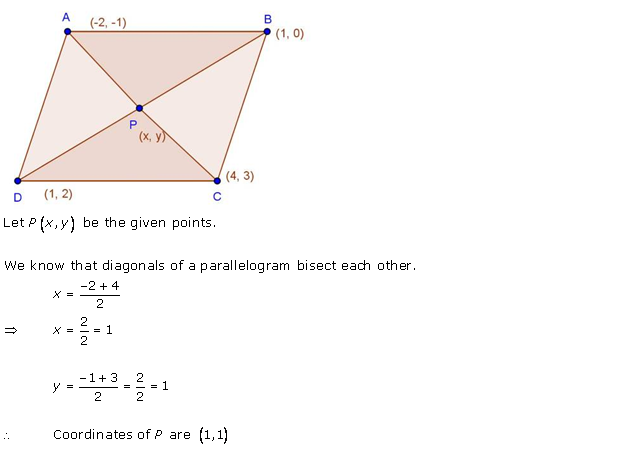
Solution 4
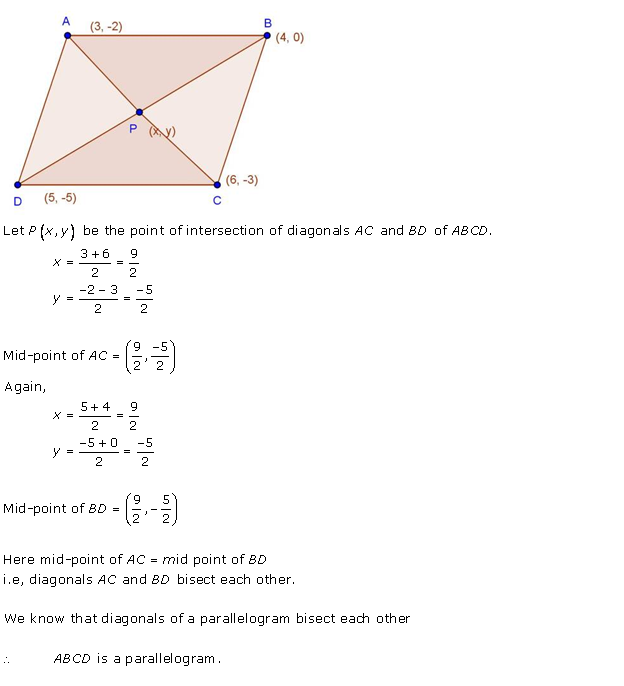
Solution 5

Solution 6

Solution 7

Solution 8
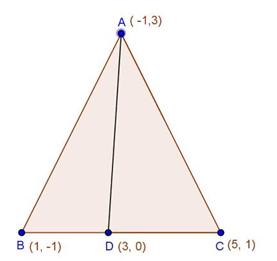

Solution 9
![]()

Solution 10
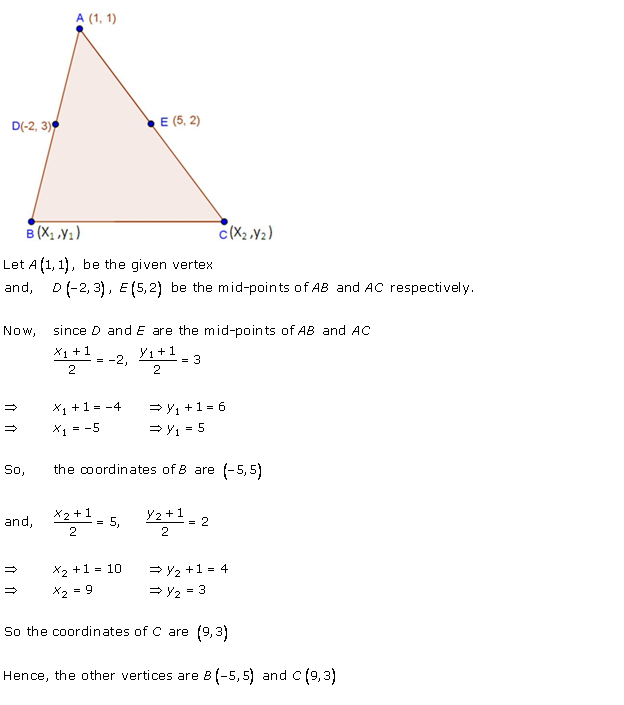
Solution 11(i)
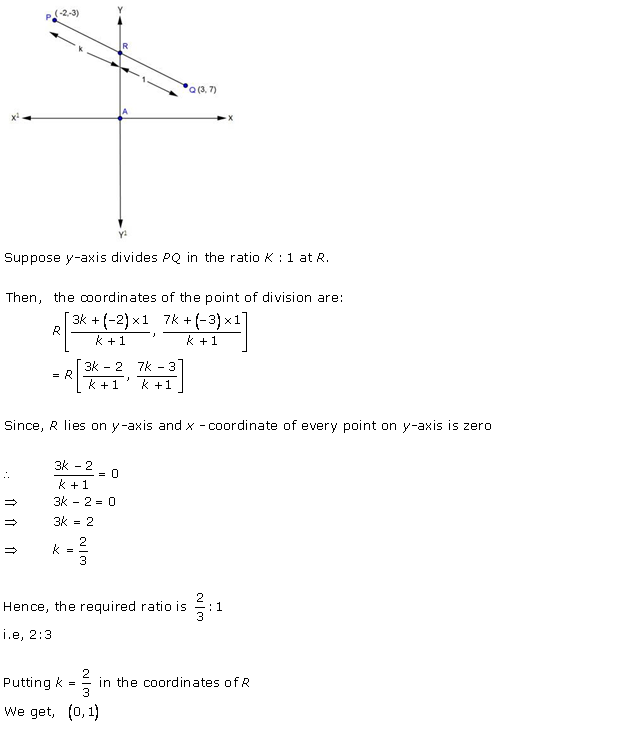
Solution 11(ii)
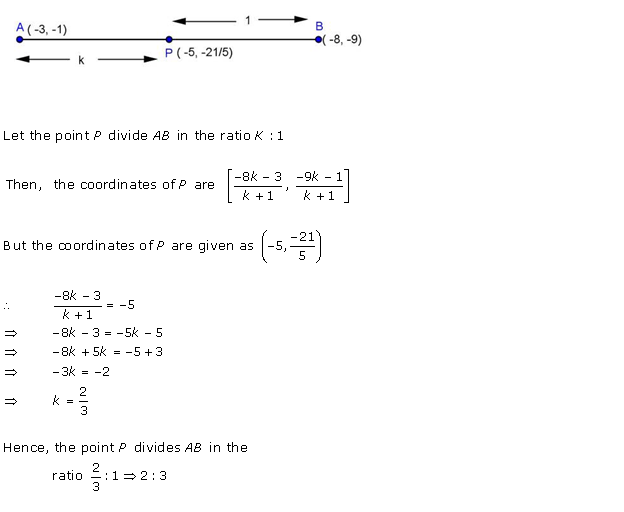
Solution 12
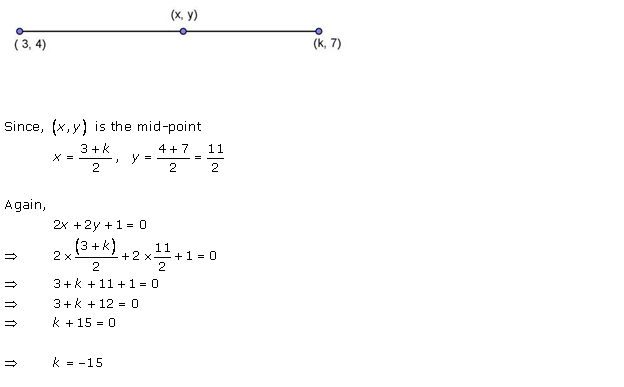
Solution 13

Solution 14


Solution 15
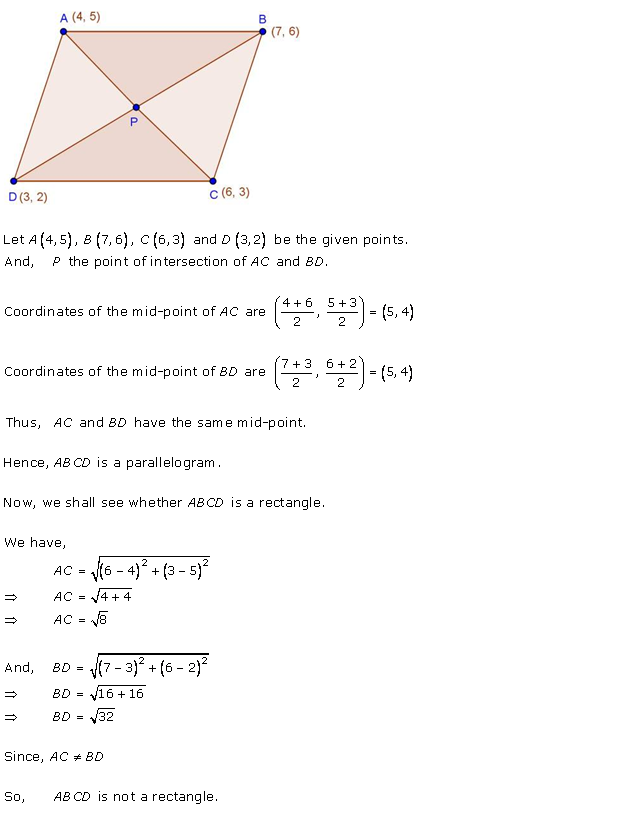
Solution 16
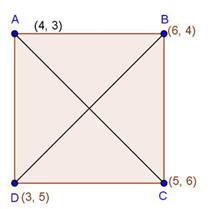
Solution 17
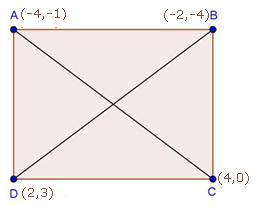

Solution 18
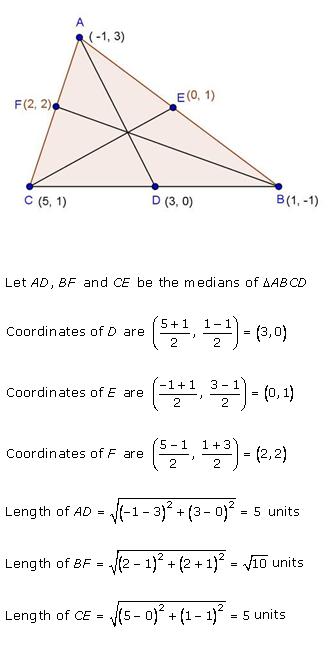
Solution 19
Let the point on the x-axis be (a, 0).
Let this point divide the line segment AB in the ratio of r : 1.
Using the section formula for the y-coordinate, we get

Solution 20

Solution 21

Solution 22
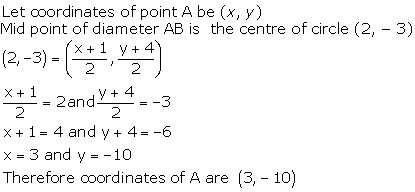
Solution 23
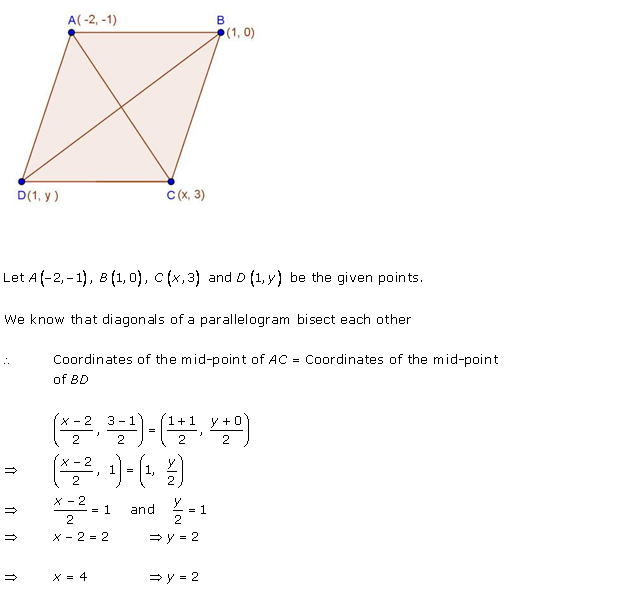
Solution 24
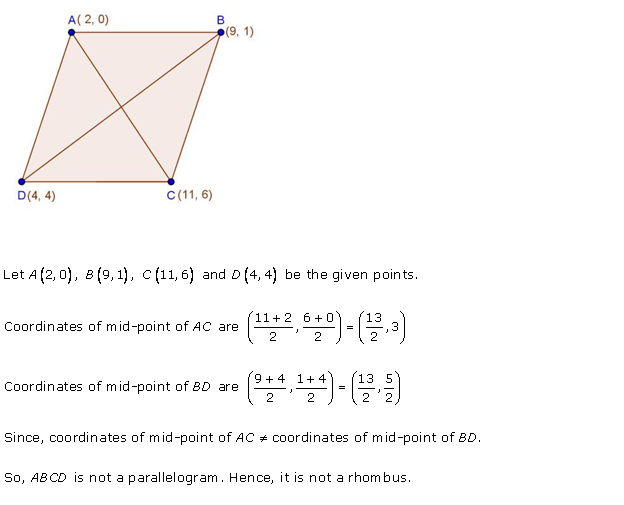
Solution 25
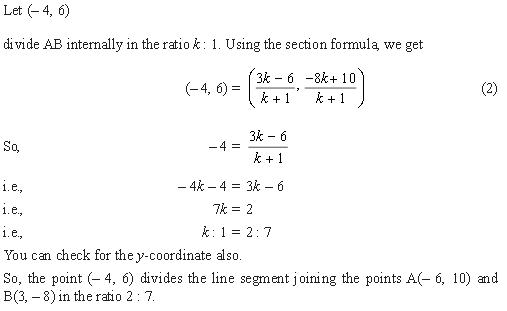
Solution 26

Solution 27
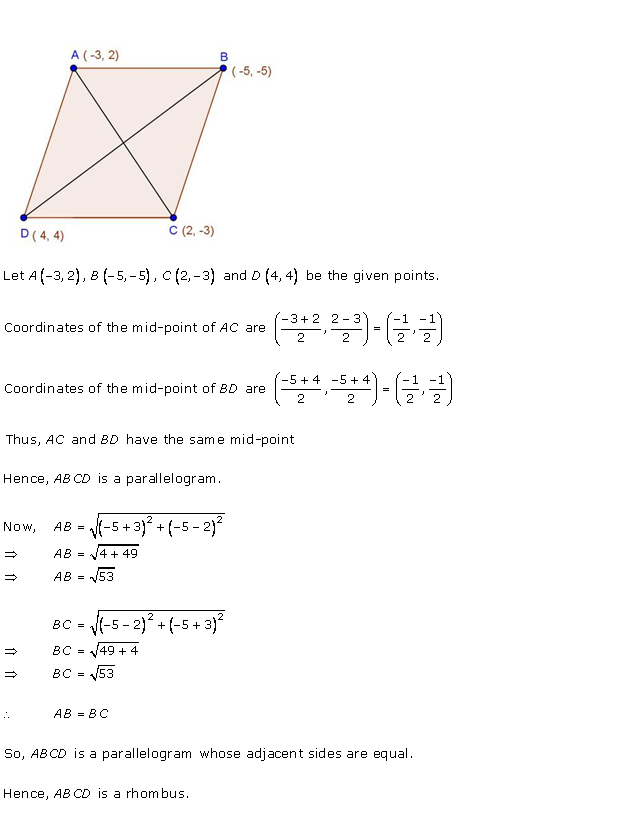
Solution 28
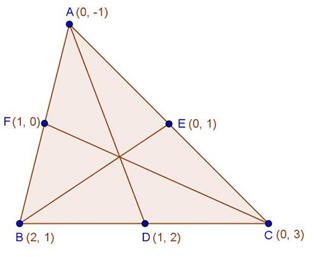

Solution 29
Let P divides the line segment AB is the ratio k: 1.
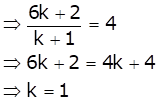
So, the ratio is 1:1.
Also, ![]()
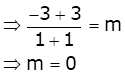
Solution 30
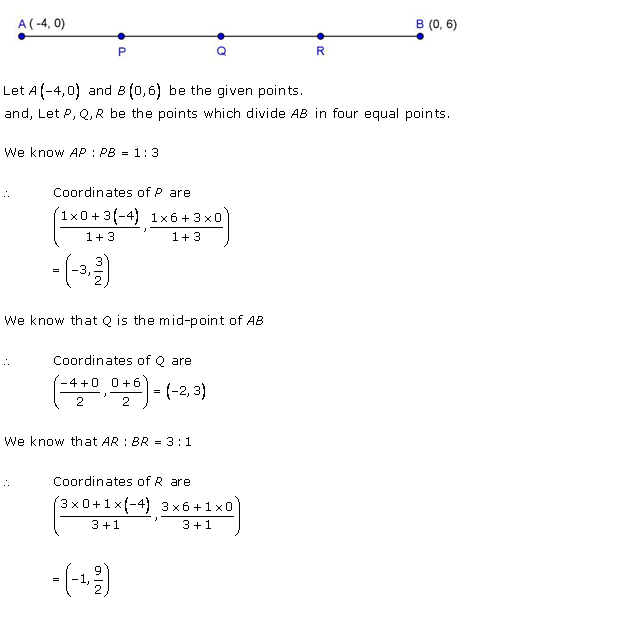
Solution 31

Solution 32

Solution 33
![]()

Solution 34
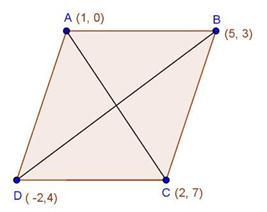

Solution 35

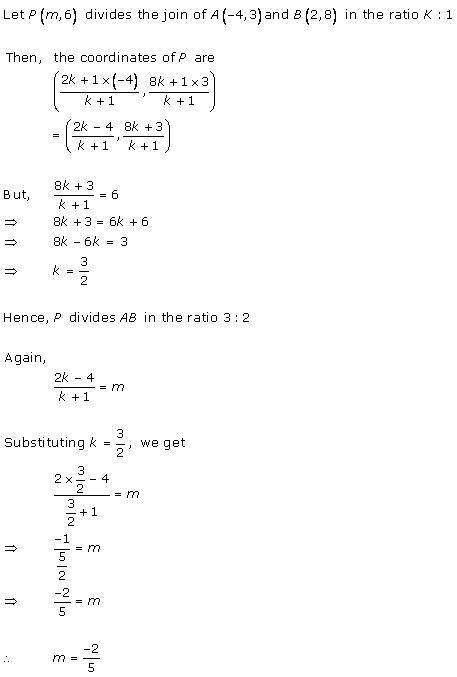
Solution 36


Solution 37
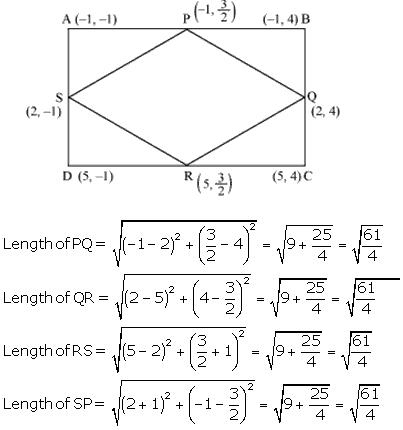
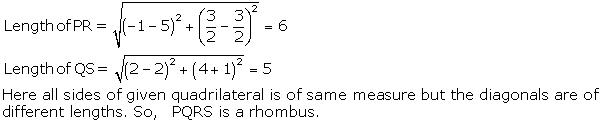
Solution 38
The difference between the x-coordinates of A and B is 6 - 1 = 5
Similarly, the difference between the y-coordinates of A and B is 7 - 2 = 5
Hence, if the line segment joining A(1, 2) and B(6, 7) is divided into 5 equal parts by the points P, Q, R and S, then the coordinates of P, Q, R and S can be found out by increasing the x and the y coordinates of A by 1 successively.
Hence, the coordinates of P are (1 + 1, 2 + 1) = (2, 3)
The coordinates of Q are (2 + 1, 3 + 1) = (3, 4)
The coordinates of R are (3 + 1, 4 + 1) = (4, 5)
Solution 39
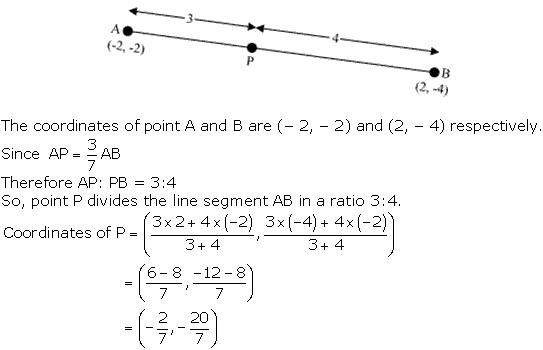
Solution 40
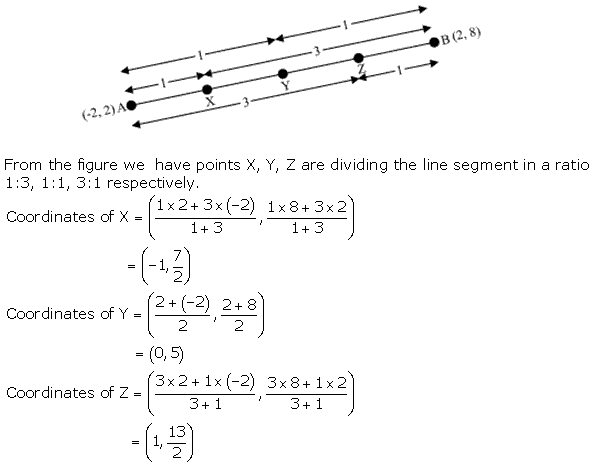
Solution 41
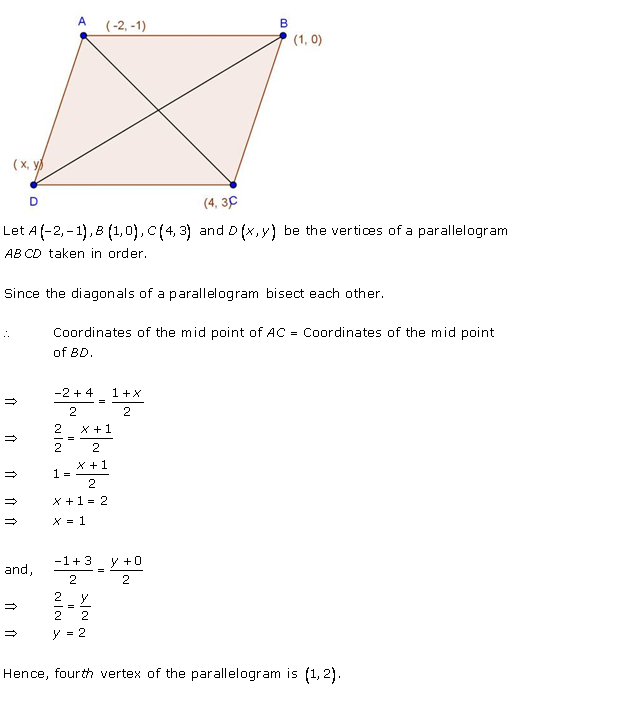
Solution 42
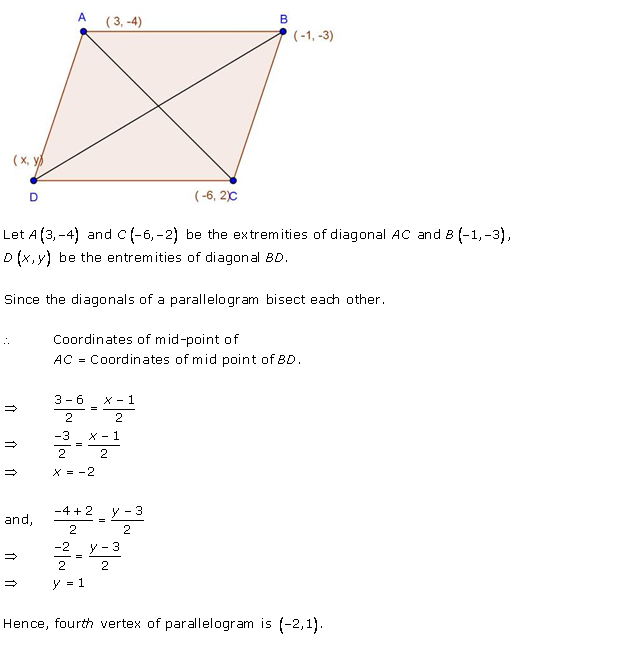
Solution 43
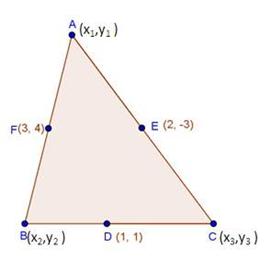


Solution 44

Solution 45
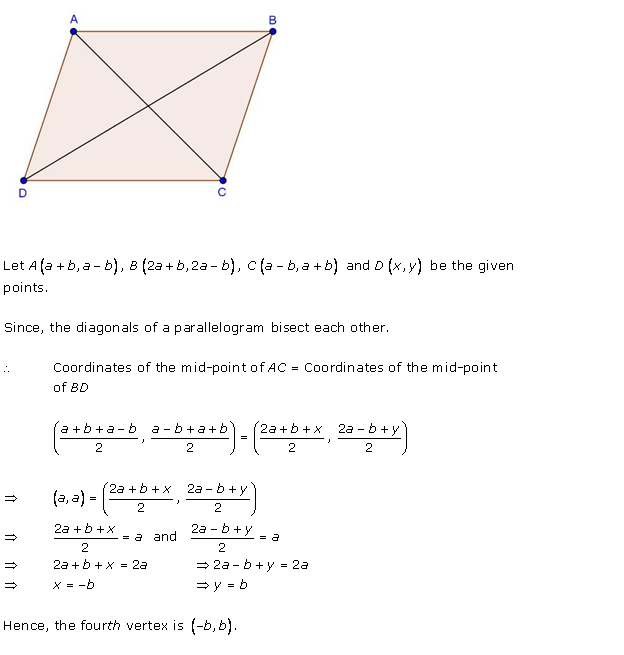
Solution 46
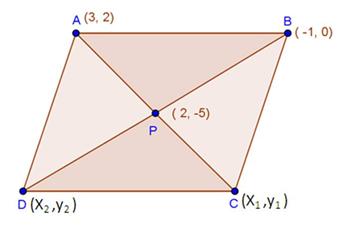

Solution 47
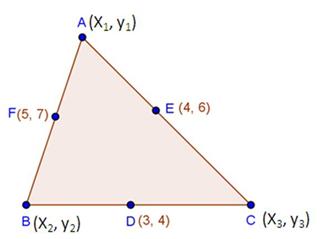
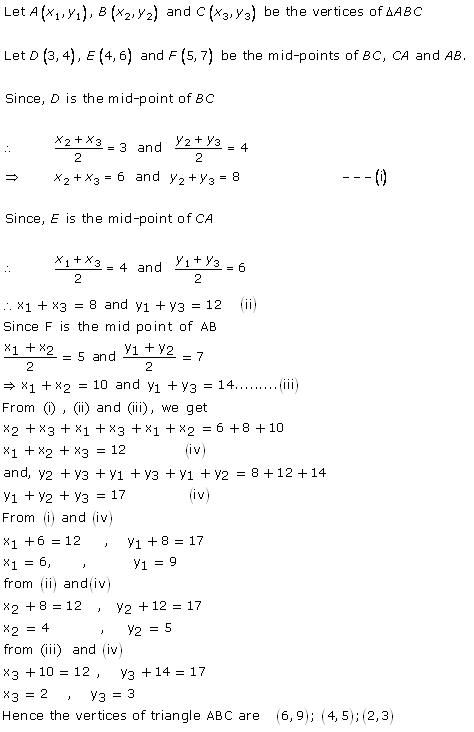
Solution 48
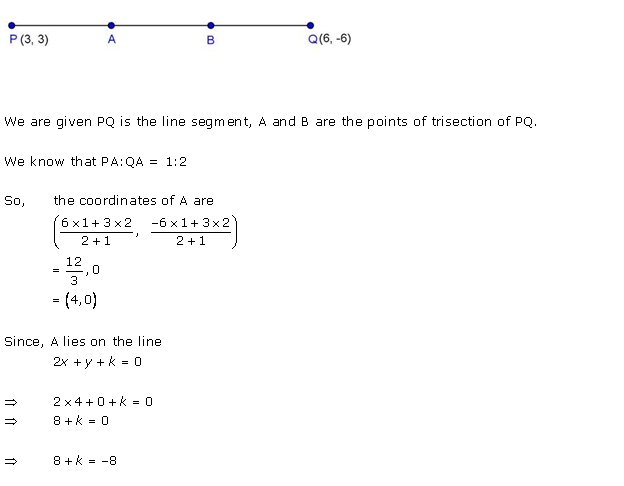
Solution 49
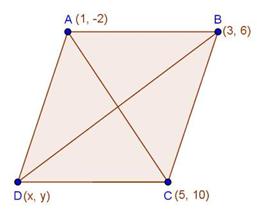

Solution 50 (i)
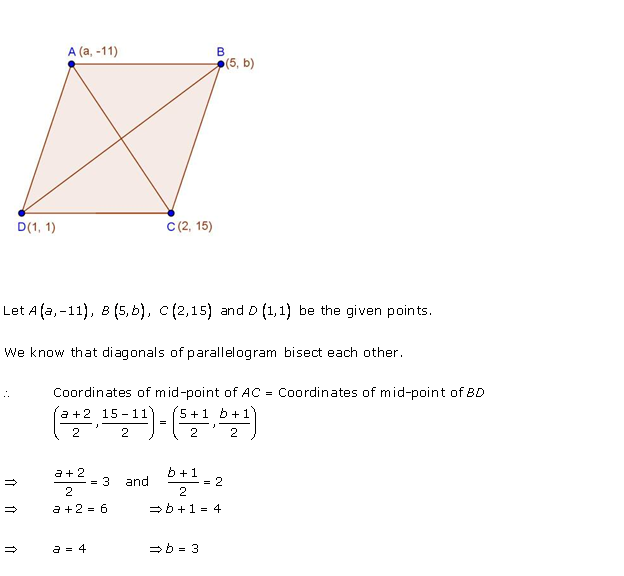
Solution 50 (ii)
Given: ABCD is a parallelogram
We know that, diagonals of a parallelogram bisect each other.
Therefore, midpoints of diagonals coincide
The midpoints of AC and BD coincide.
Solution 51
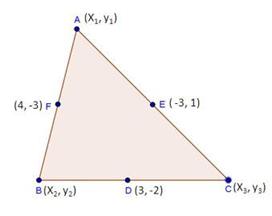
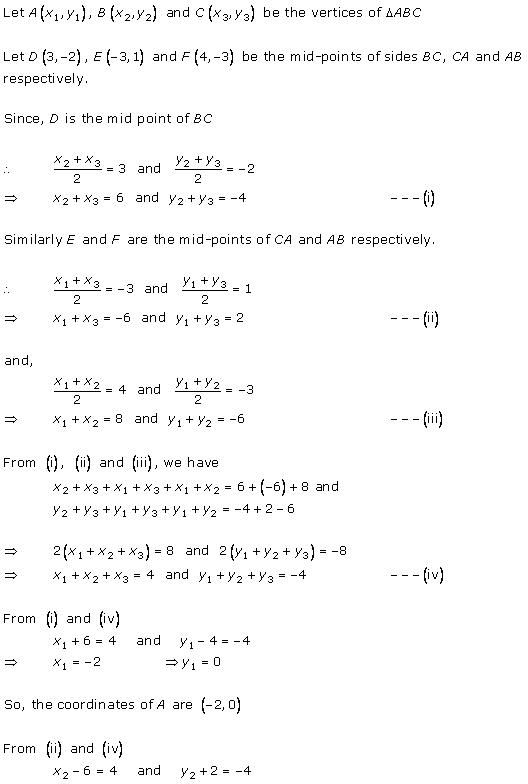

Solution 52 (i)
As P and Q trisect AB and P is near to A.
Therefore, P divides AB in the ratio 1:2.
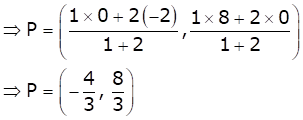
Also, Q divides AB in the ration 2:1.
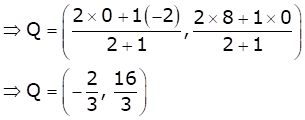
Solution 52 (ii)


Solution 53
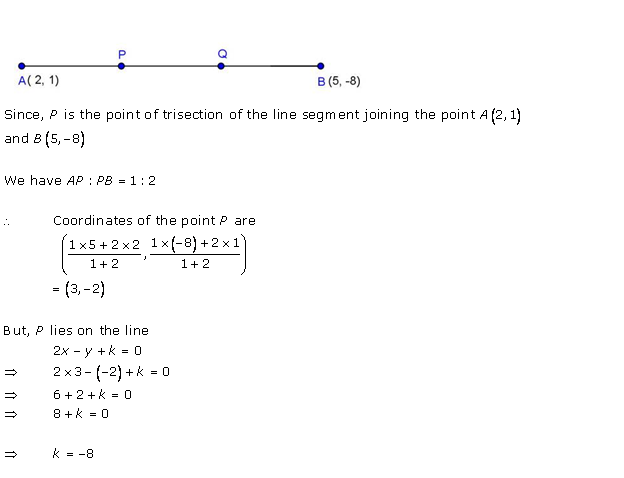
Solution 54
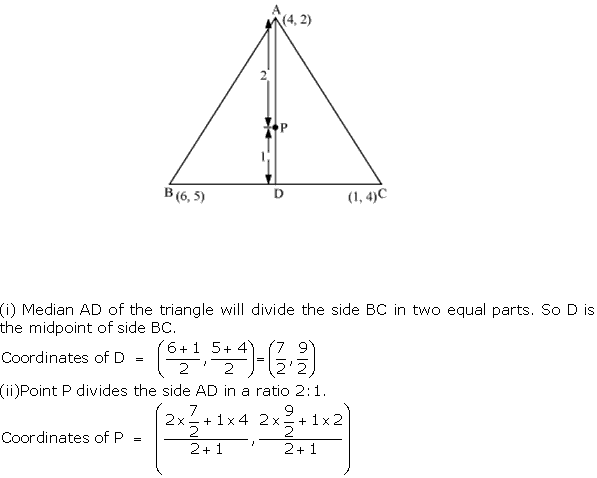

Solution 55
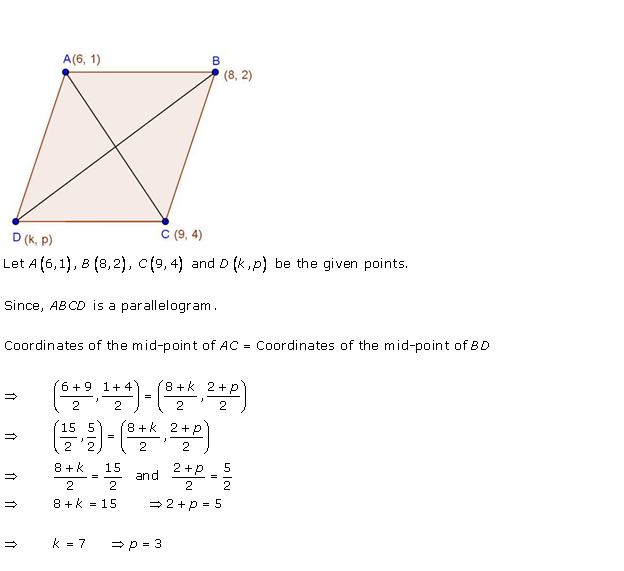
Solution 56
Given points are A(3,-5) and B(-4,8).
P divides AB in the ratio k : 1.
Using the section formula, we
have:
Coordinate of point P are {(-4k+3/k+1)(8k-5/k+1)}
Now it is given, that P lies on the line x+y = 0
Therefore,
-4k+3/k+1 + 8k-5/k+1 =0
=> -4k+3+8k-5 =0
=> 4k -2 =0
=> k=2/4
=> k=1/2
Thus, the value of k is 1/2.
Solution 57

Solution 58
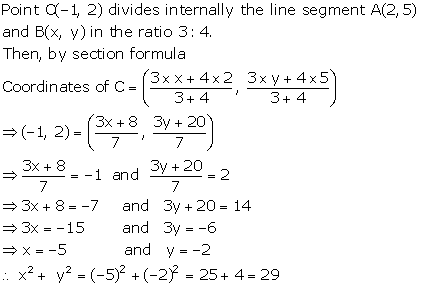
Solution 59

Solution 60

Co-ordinate Geometry Exercise Ex. 6.4
Solution 1(i)

Solution 1(ii)

Solution 2

Solution 3

Solution 4

Solution 5
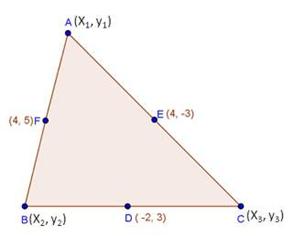

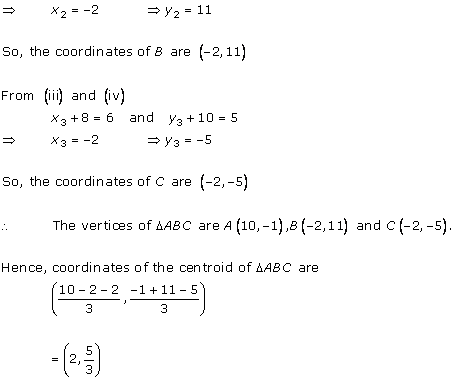
Solution 6
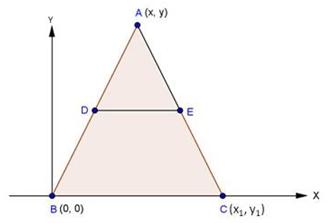

Solution 7
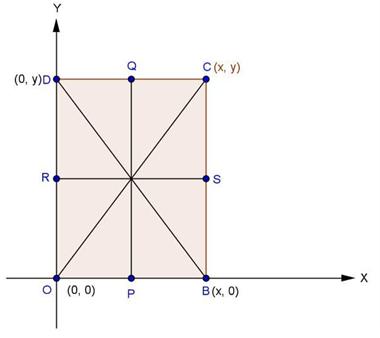

Solution 8


Solution 9

Solution 10
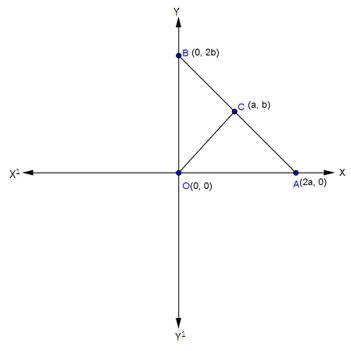

Co-ordinate Geometry Exercise Ex. 6.5
Solution 1
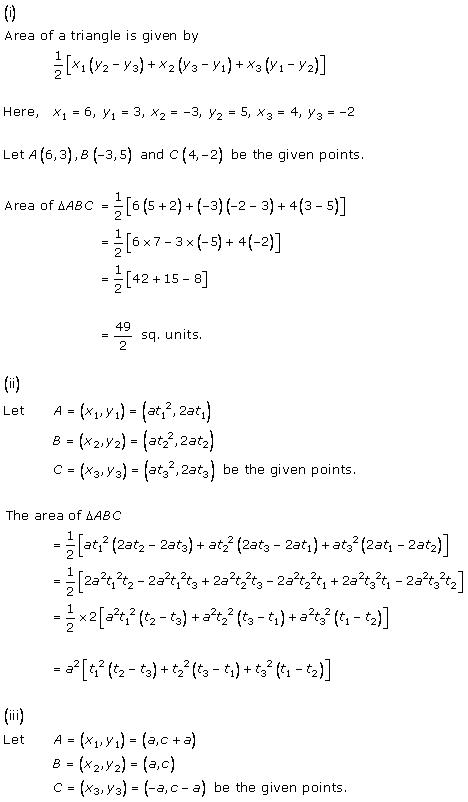

Solution 1 (iv)
Area of triangle with vertices (x1, y1), (x2, y2) and (x3, y3) is
![]()
Therefore, area of triangle with given vertices is
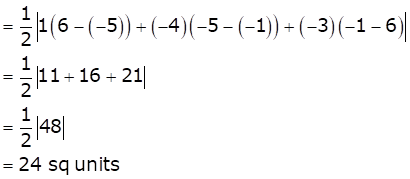
Hence, the area of triangle will be 24 sq. units.
Solution 1 (v)
Area of triangle with vertices (x1, y1), (x2, y2) and (x3, y3) is
![]()
Therefore, area of triangle with given vertices is
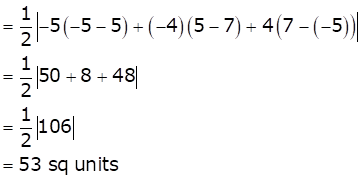
Hence, the area of triangle will be 53 sq. units.
Solution 2(i)
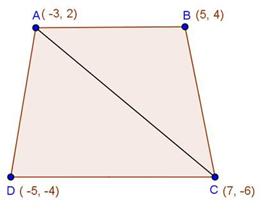
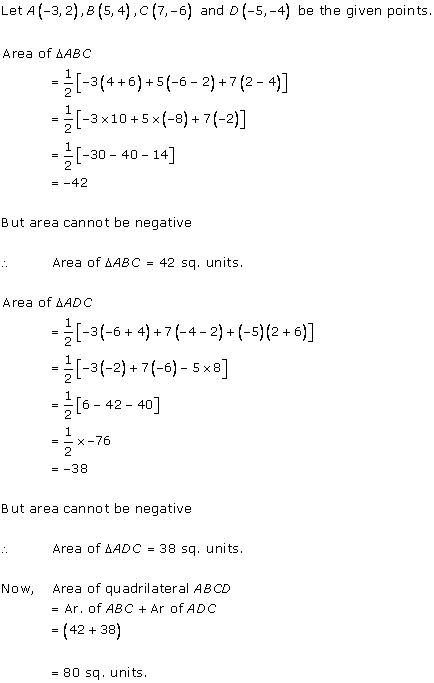
Solution 2(ii)

Solution 2(iii)

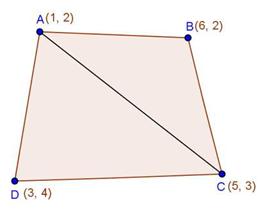
Solution 3
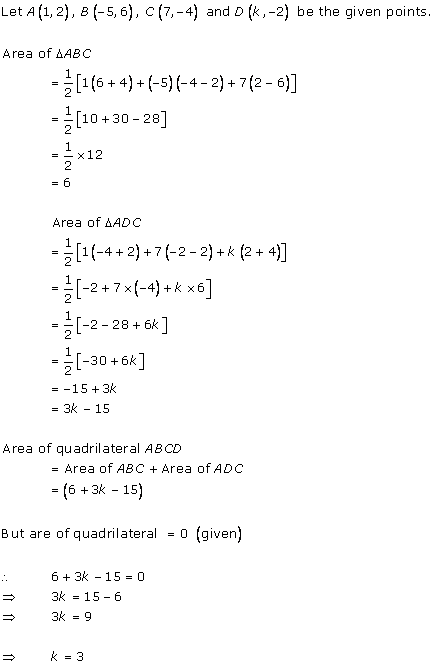
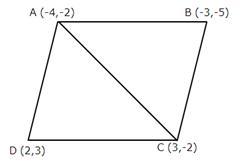
Solution 4
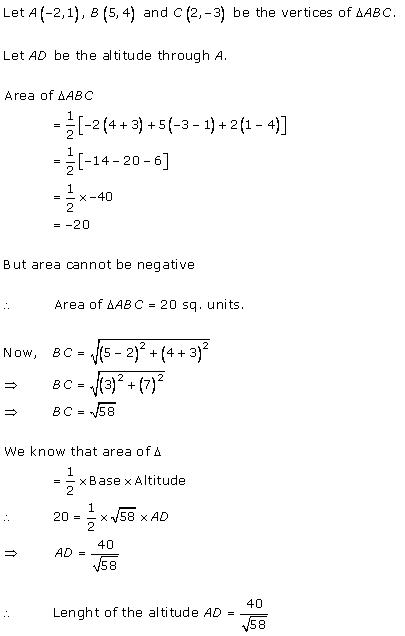
Solution 5
Solution 6
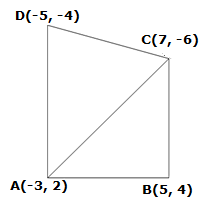
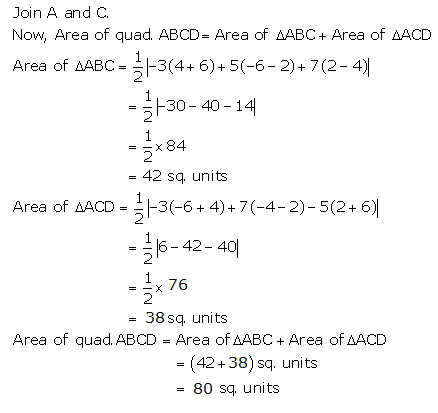
Solution 7

Solution 8
![]()
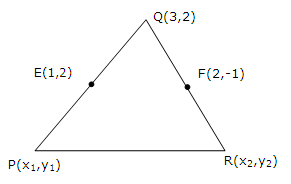
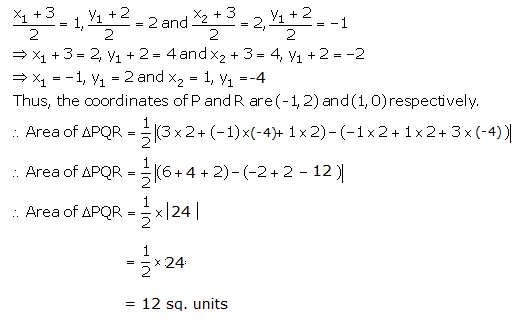
Solution 9
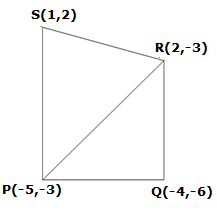

Solution 10

Solution 11
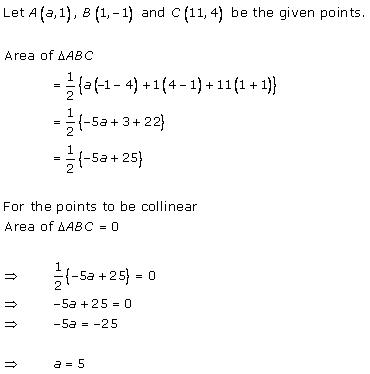
Solution 12
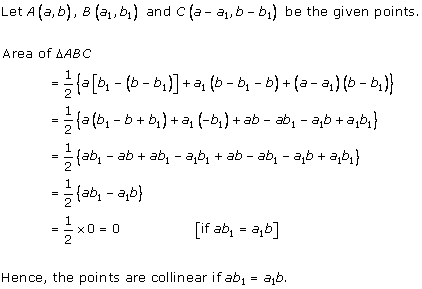
Solution 13 (i)
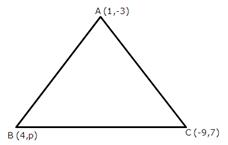

Solution 13 (ii)
Area of triangle with vertices (x1, y1), (x2, y2) and (x3, y3) is
![]()
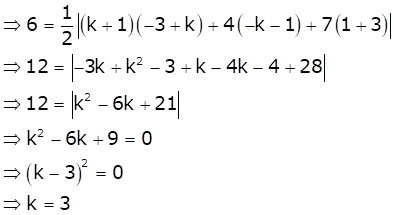
Hence, the value of k is 3.
Solution 14
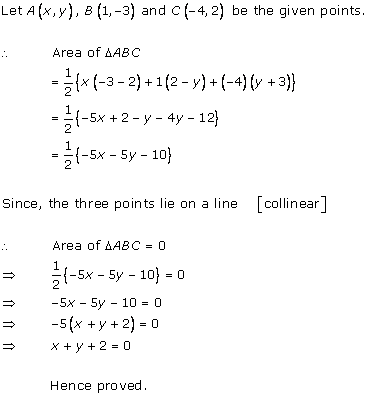
Solution 15

Solution 16

Solution 17
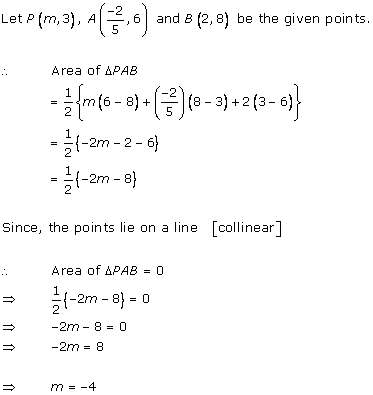
Solution 18
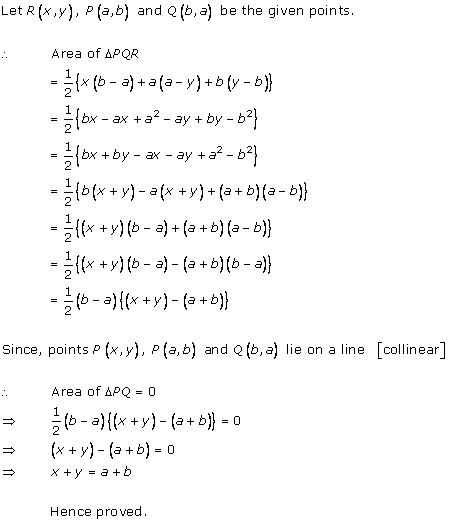
Solution 19

Solution 20

Solution 21
Let the points (a, a2), (b, b2), (0, 0) represent a triangle. If we can prove that the area of the triangle so formed is not equal to zero, then we can prove that the points (a, a2), (b, b2), (0, 0) are never collinear.
Area of a triangle is given by
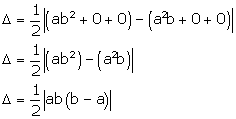
Now b≠a≠0.
So,
b - a≠0,
Δ≠0
Thus, points (a, a2), (b, b2), (0, 0) are never collinear.
Solution 22
Area of a triangle is given by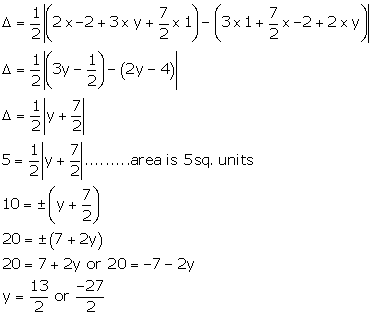
Solution 23
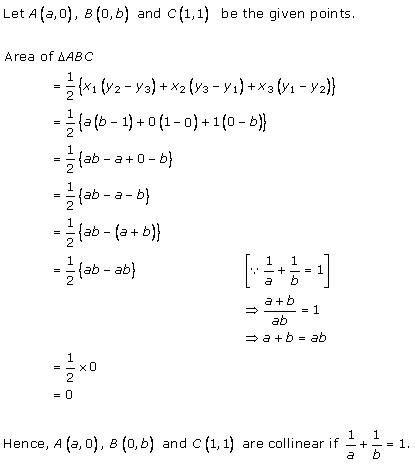
Solution 24
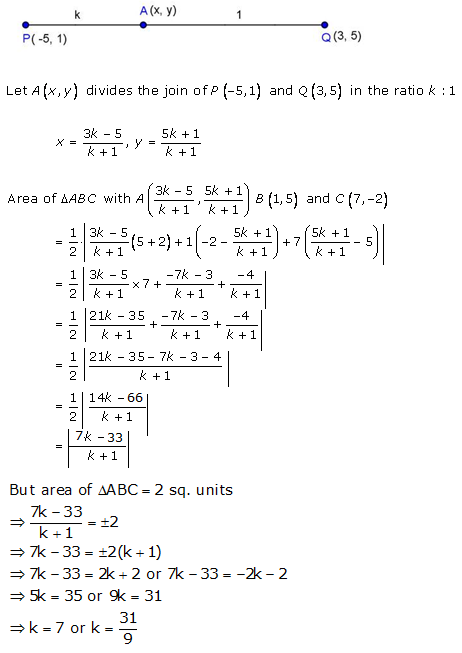
Solution 25
Solution 26

Solution 27
Solution 28

Solution 29

Solution 30
Let the points be A, B and C respectively.
If A, B and C are collinear, then the area of ∆ABC is zero.
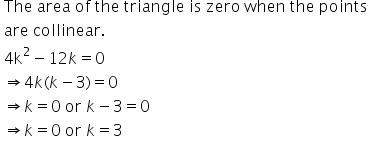
Solution 31
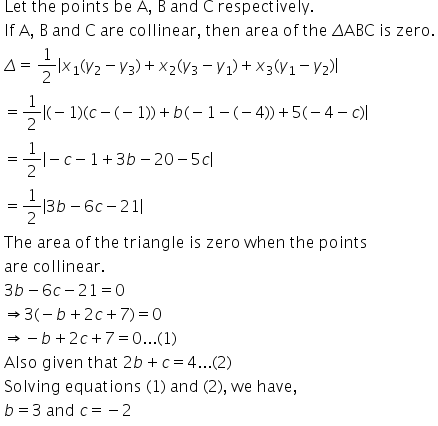
Solution 32
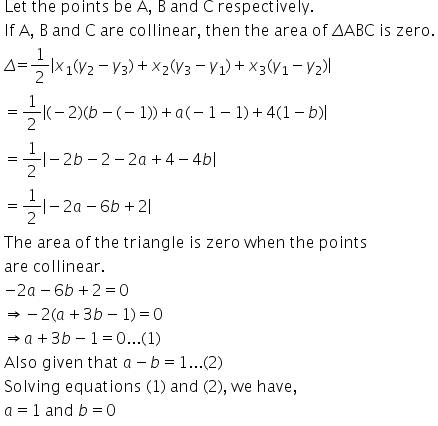
Solution 33
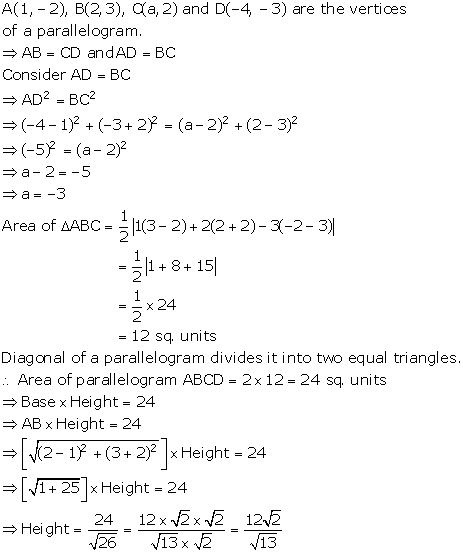
Solution 34

Solution 35
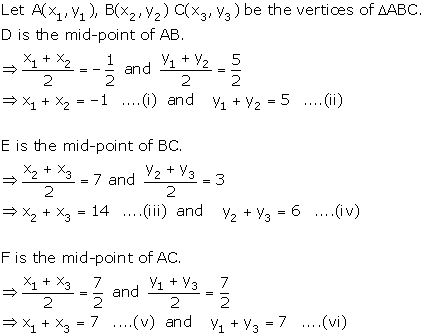
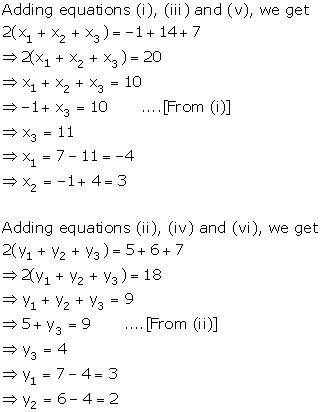
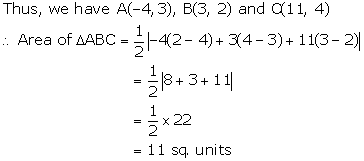
Co-ordinate Geometry Exercise 6.63
Solution 1

Solution 2

Solution 3
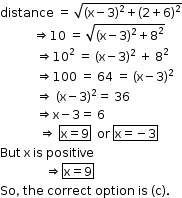
Solution 4
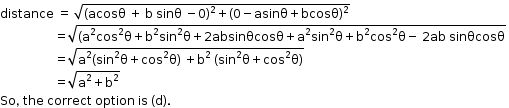
Solution 5
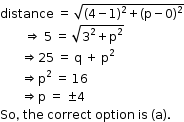
Solution 6

Solution 7
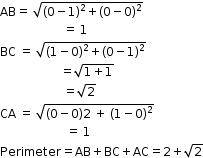
So, the correct option is (d).
Solution 8
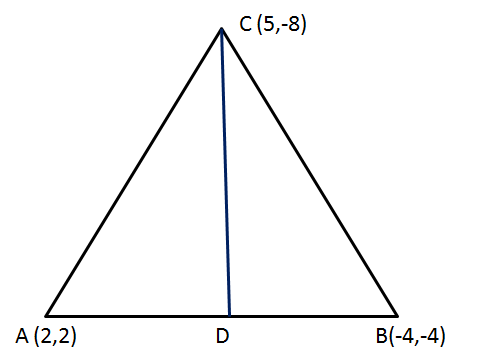
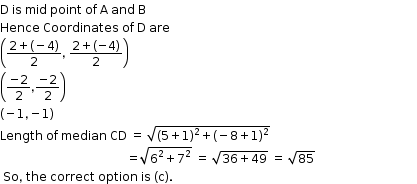
Solution 9
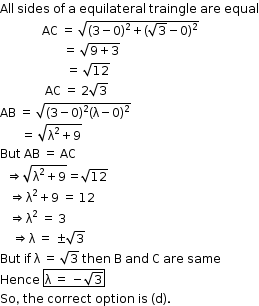
Solution 10

Co-ordinate Geometry Exercise 6.64
Solution 11

Solution 12
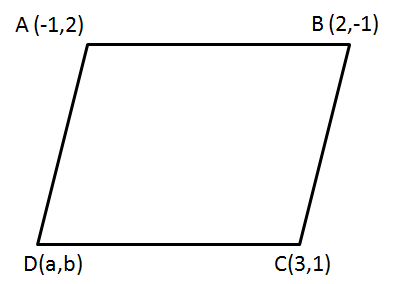

Note: The answer does not match the options.
Solution 13
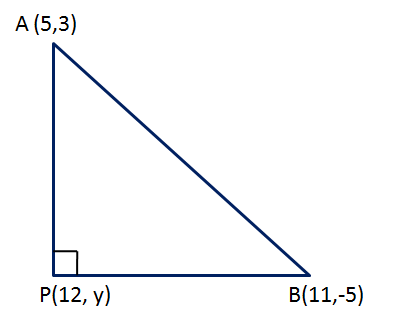
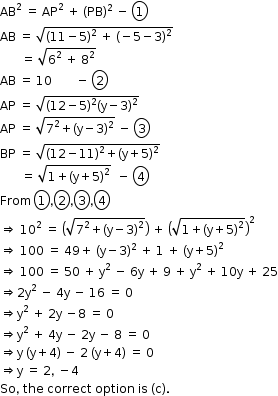
Solution 14
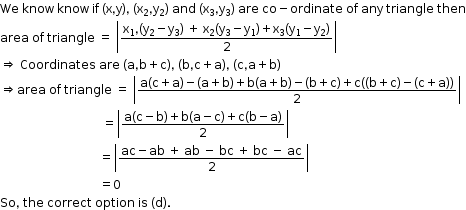
Solution 15
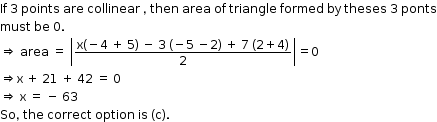
Solution 16

Solution 17

Solution 18

Solution 19
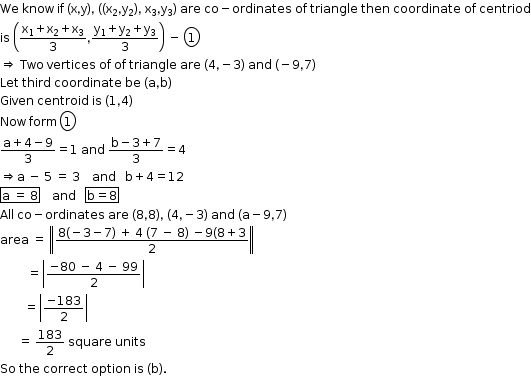
Solution 20
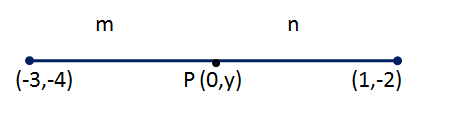

Solution 21
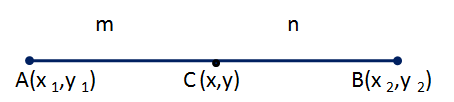

Solution 22
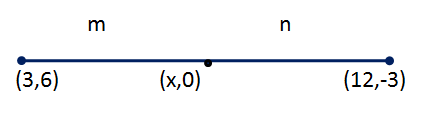

Solution 23
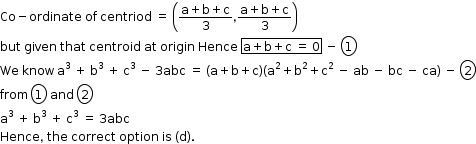
Solution 25

Solution 24
As the points A, B and C are collinear, then the area formed by these three points is 0.
Area of triangle with vertices (x1, y1), (x2, y2) and (x3, y3) is
![]()
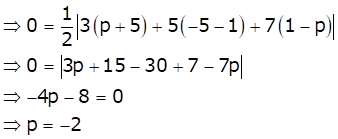
Hence, the value of p is -2.
Co-ordinate Geometry Exercise 6.65
Solution 26
We know, distance of point (x, y) from x-axis is y.
Hence, distance of point (4, 7) from x-axis is 7.
Hence, correct option is (b).
Solution 27
We know distance of point (x, y) from y-axis is x.
Hence distance of point (4, 7) from y-axis is 4.
Hence, correct option is (a).
Solution 28
Given P is a point on x-axis
Hence P = (x, 0)
Distance from the origin is 3
Hence P = (3, 0)
Given Q is a point on y-axis
So Q is (0, y)
Given that OP = OQ
implies OQ = 3
Distance of Q from the origin is 3
Hence y = 3
implies Q = (0, 3)
Hence, correct option is (a).
Solution 29

Solution 30
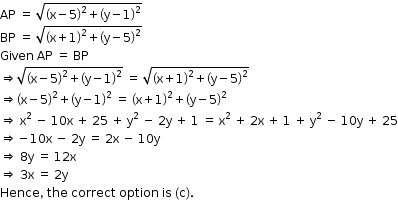
Solution 31

Solution 32
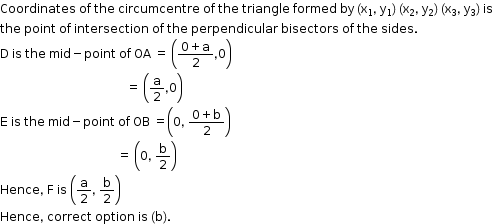
Solution 33

Solution 34

Solution 35
The Centroid of the triangle is given by
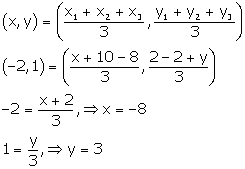
x=-8 and y=3 satisfy(a) 3x + 8y = 0.
Solution 36
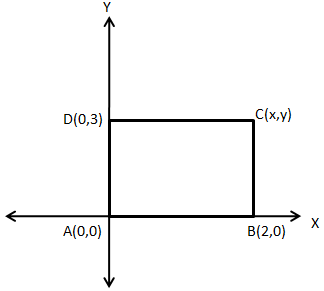

Solution 37

Solution 38

Solution 39

Co-ordinate Geometry Exercise 6.66
Solution 40
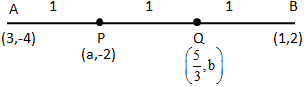
Solution 41
![]()

Solution 42
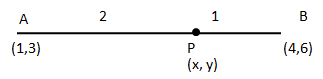
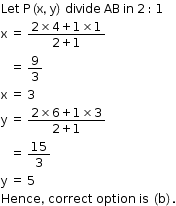
Solution 43

Solution 44
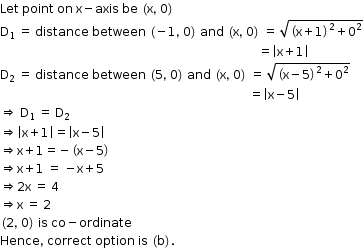
Solution 45

Solution 46

Solution 47

Solution 48

Co-ordinate Geometry Exercise 6.67
Solution 49
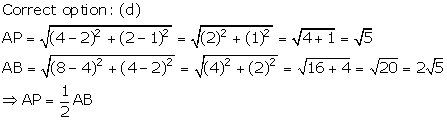
Solution 50
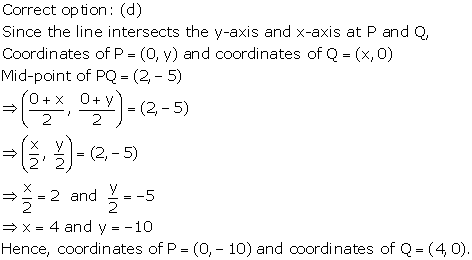
Solution 51
As the point (k, 0) divides the line segment AB in the 1:2
![]()
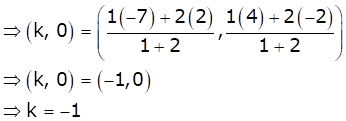
Hence, option (d) is correct.