Chapter 12 Heights and Distances
Class 10th R. D. Sharma Maths Solution
CBSE Class 10 Maths
R. D. Sharma Solution
Some Applications of Trigonometry Exercise Ex. 12.1
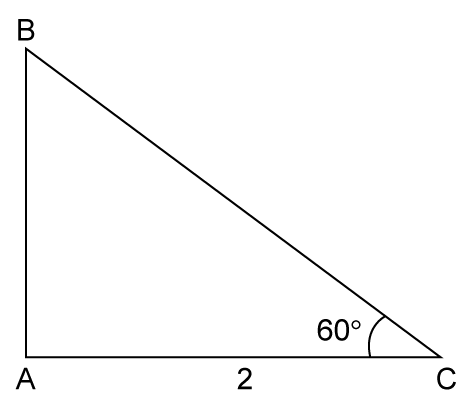
Solution 1
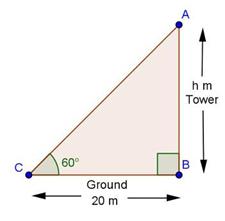

Solution 2
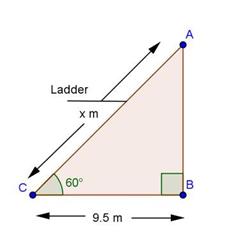

Solution 3
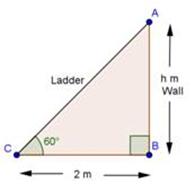
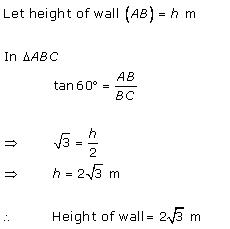
Solution 4
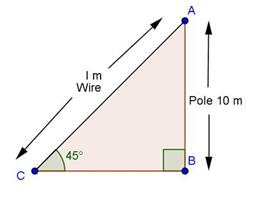

Solution 5
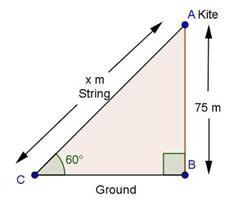
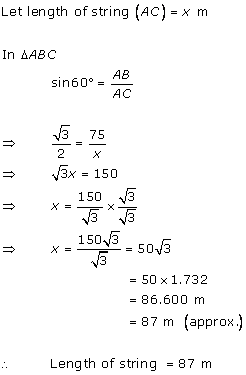
Solution 6
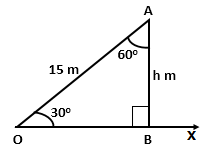

Solution 7
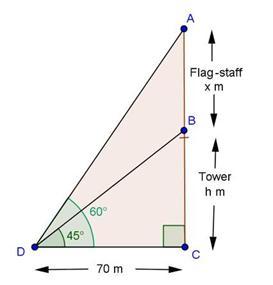

Solution 8
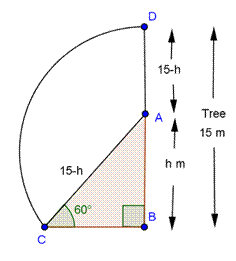

Solution 9
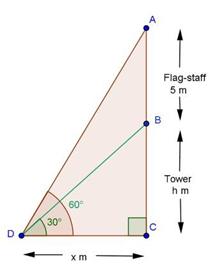
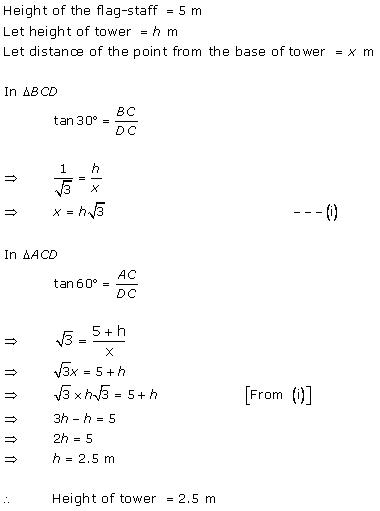
Solution 10
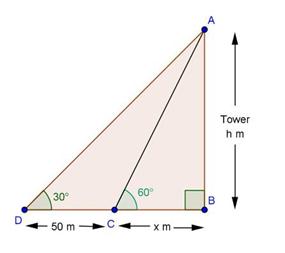

Solution 11
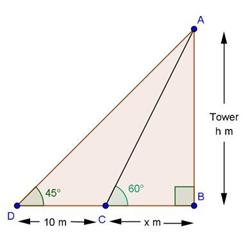

Solution 12
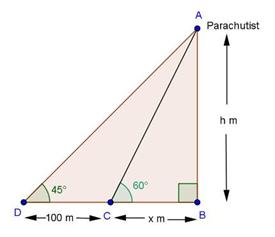

Solution 13
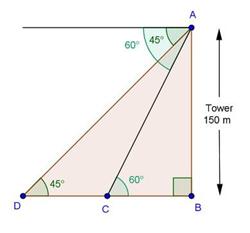

Solution 14
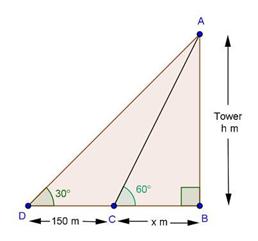

Solution 15
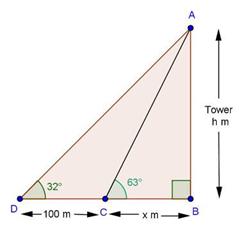

Solution 16
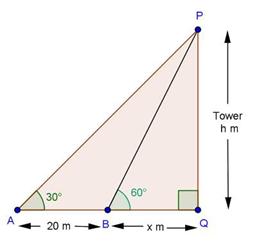

Solution 17
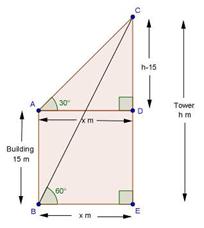

Solution 18
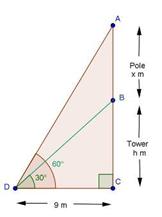
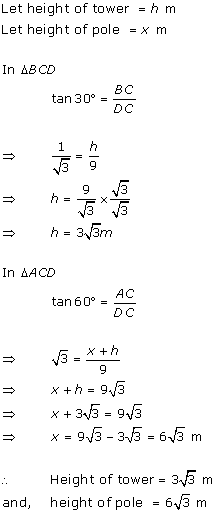
Solution 19
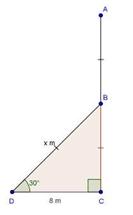
Solution 20
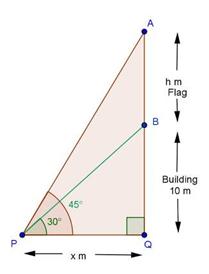
Solution 21
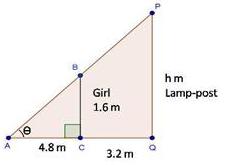


Solution 22
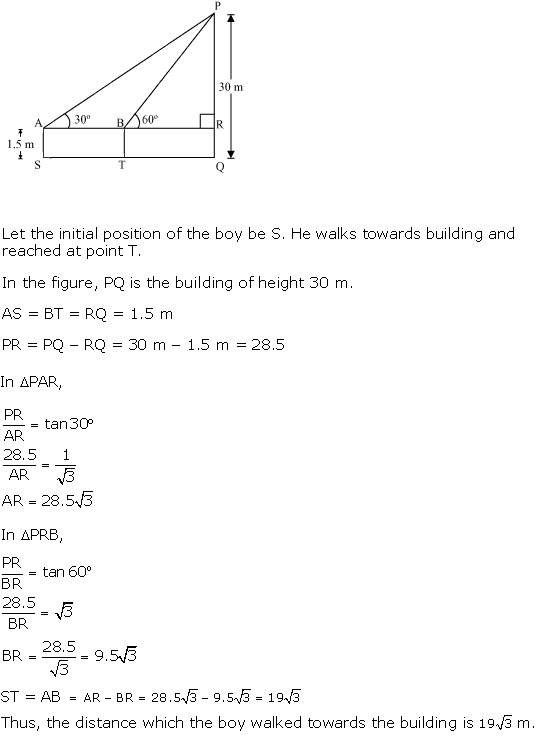
Solution 23
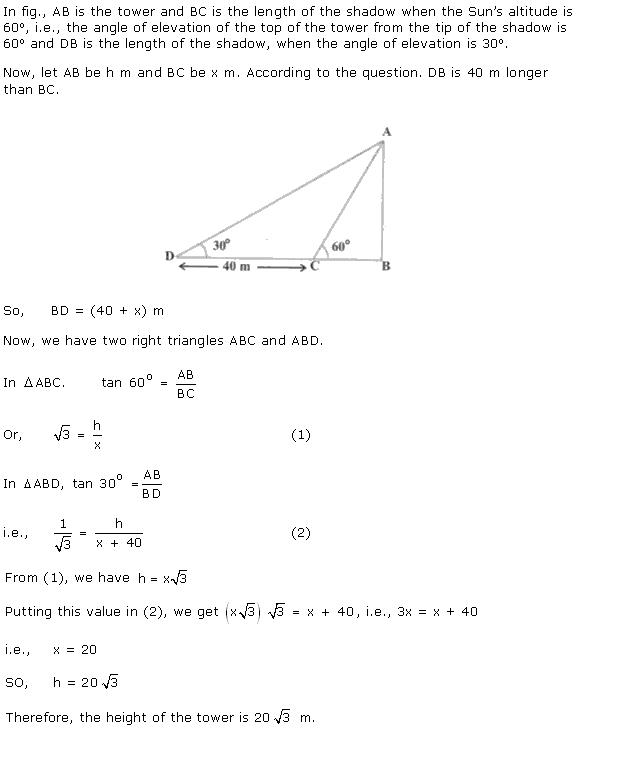
Solution 24
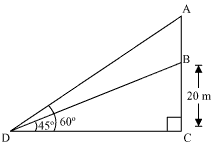
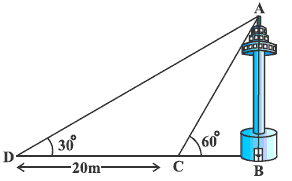
Let BC be the building, AB be the transmission tower, and D be the point on ground from where elevation angles are to be measured.
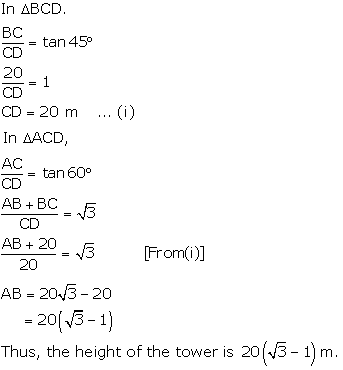
Solution 25

Solution 26
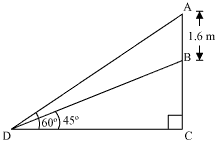
Let AB be the statue, BC be the pedestal and D be the point on ground from where elevation angles are to be measured.
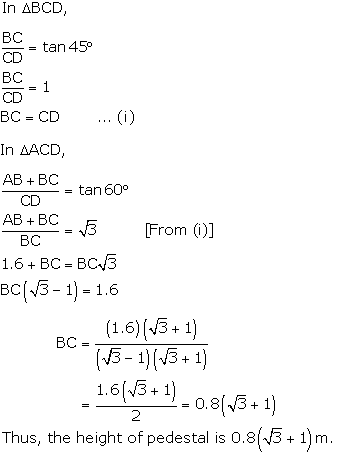
Solution 27
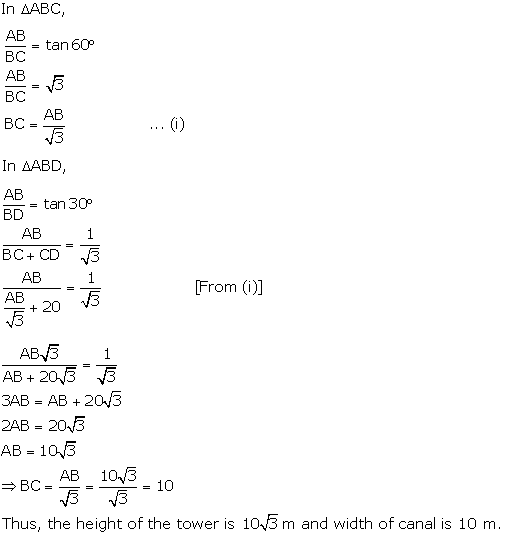
Solution 28
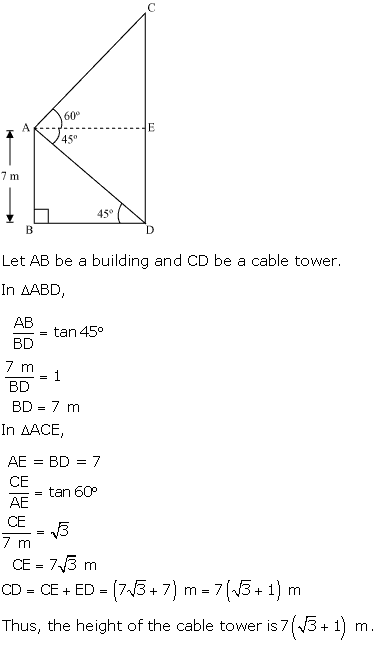
Solution 29
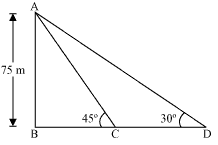
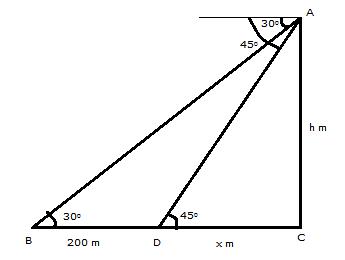
Let AB be the lighthouse and the two ships be at point C and D respectively.
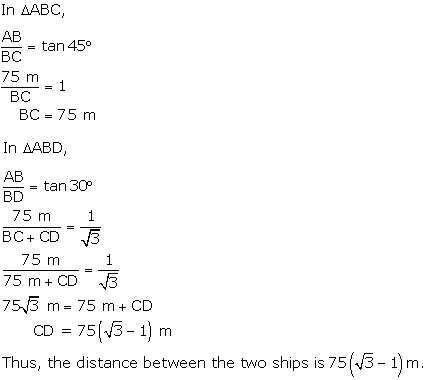
Solution 30
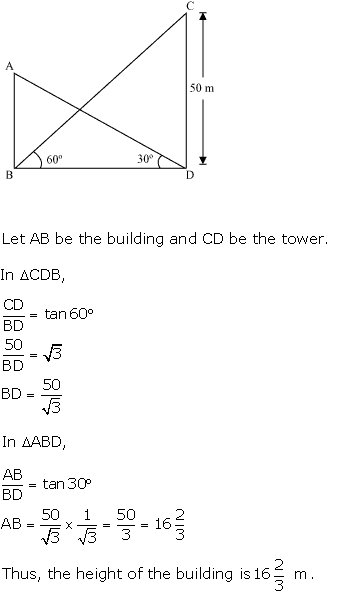
Solution 31
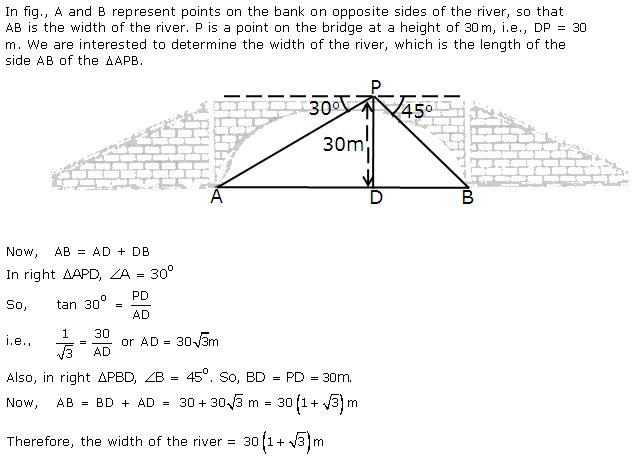
Solution 32
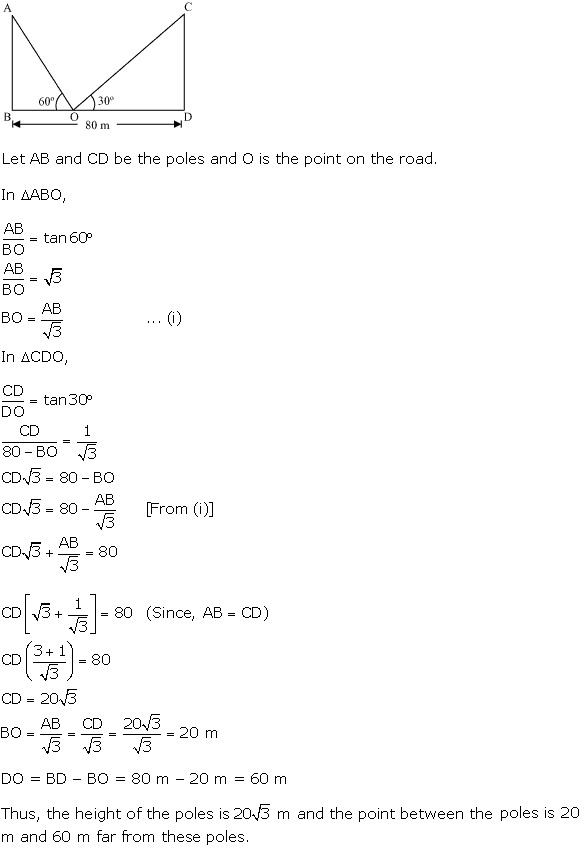
Solution 33
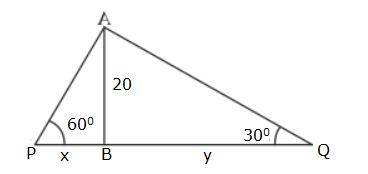
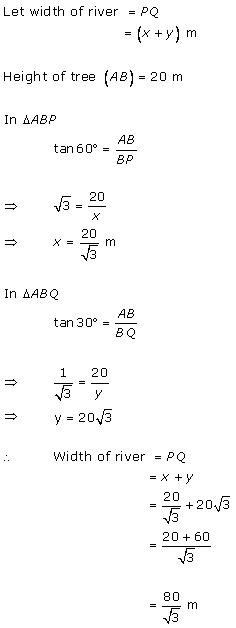
Solution 34
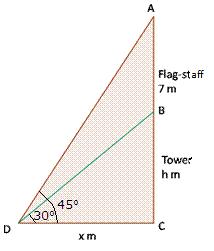
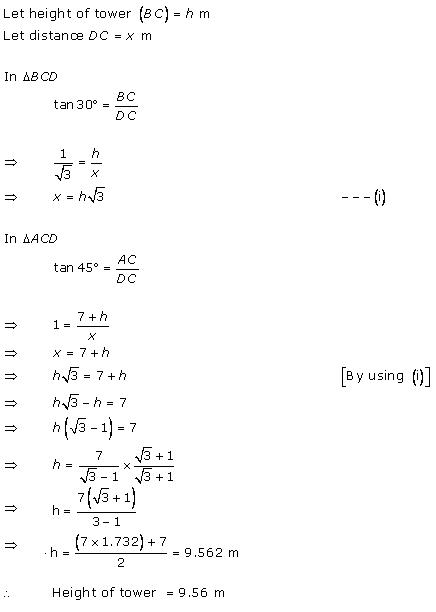
Solution 35
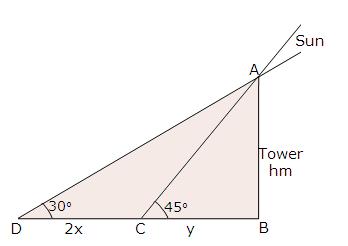
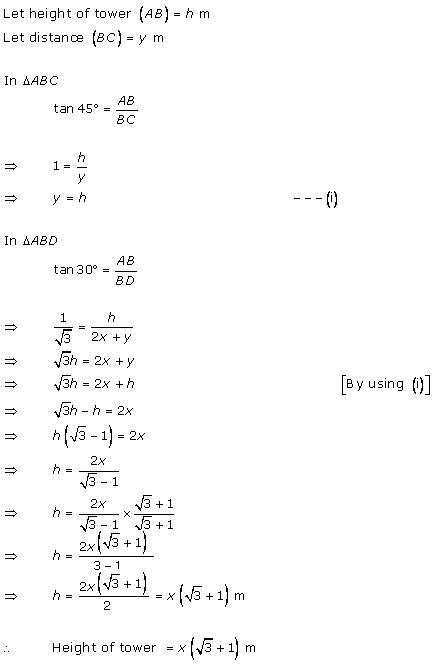
Solution 36
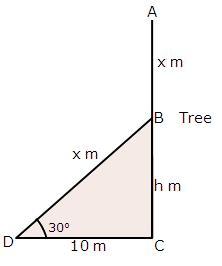
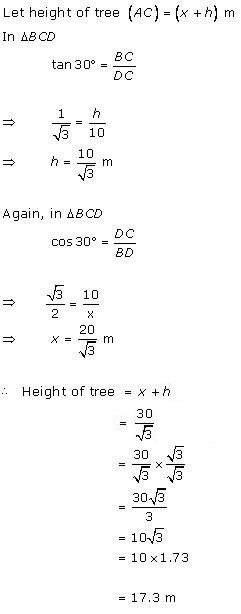
Solution 37
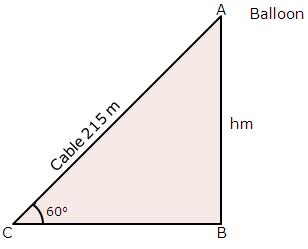

Solution 38
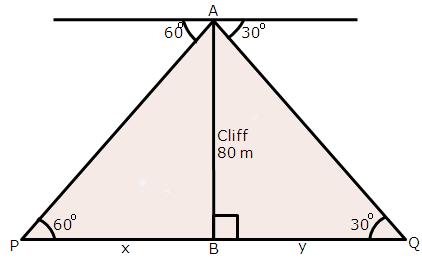

Solution 39
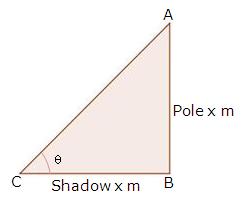

Solution 40
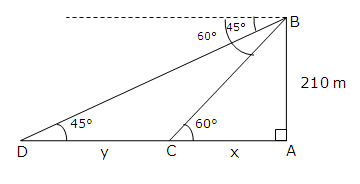

Solution 41
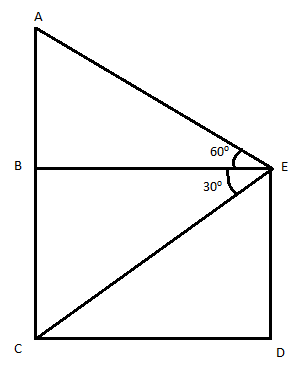
Let AC = h be the height of the chimney.
Height of the tower = DE = BC = 40 m
In ∆ABE,
![]()
![]()
∴AB = BE√3….(i)
In ∆CBE,
tan 30° = ![]()
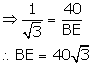
Substituting BE in (i),
AB = 40√3 × √3
= 120 m
Height of the chimney = AB + BC = 120 + 40 = 160 m
Yes, the height of the chimney meets the pollution control norms.
Solution 42
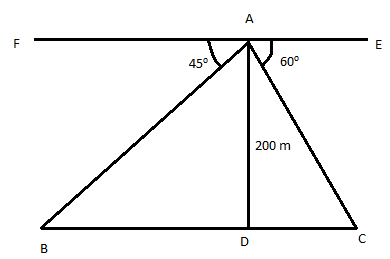
Let the ships be at B and C.
In D ABD,
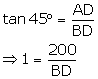
∴ BD = 200 m
In D ADC,
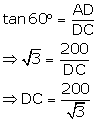
Distance between the two ships = BC = BD + DC
![]()
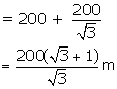
Solution 43
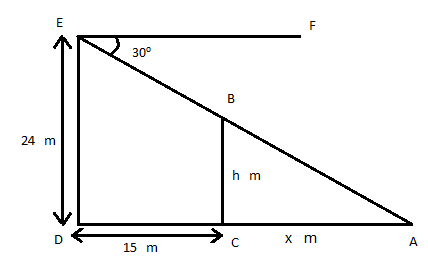
Here m∠CAB = m∠FEB = 30°.
Let BC = h m, AC = x m
In D ADE,
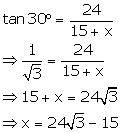
In D BAC,
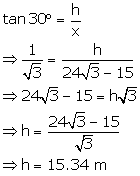
Height of the second pole is 15.34 m
Solution 44
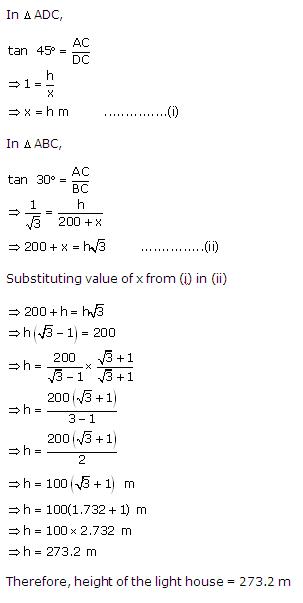
Solution 45
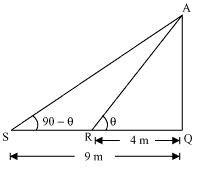
Let AQ be the tower and R, S respectively be the points which are 4m, 9m away
from base of tower.
As
the height can not be negative, the height of the tower is 6 m.
Solution 46
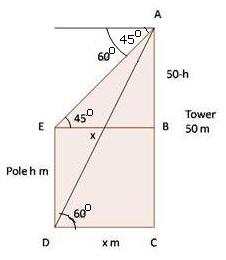

Solution 47
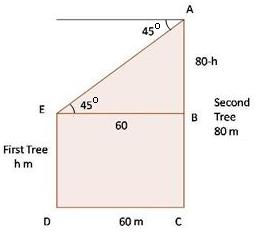

Solution 48
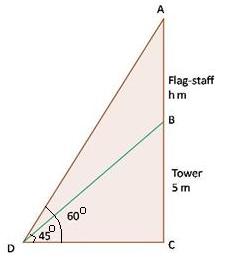
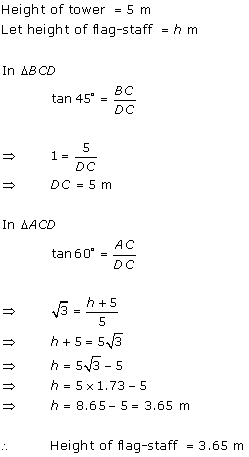
Solution 49
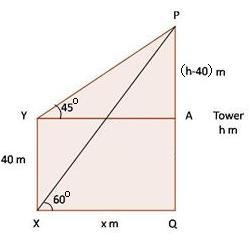

Solution 50
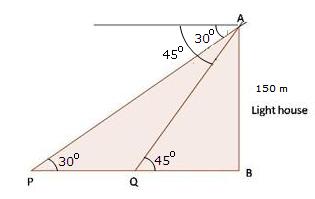

Solution 51
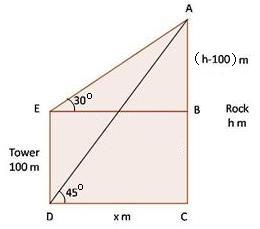

Solution 52
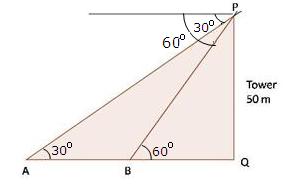

Solution 53
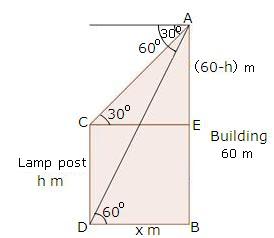
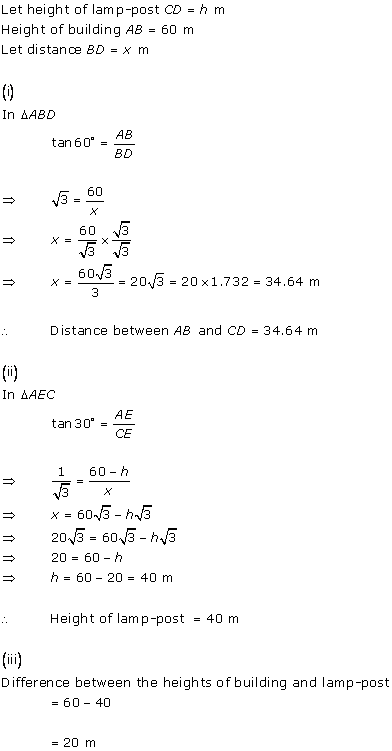
Solution 54
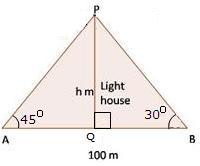

Solution 55
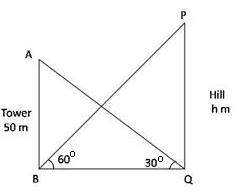
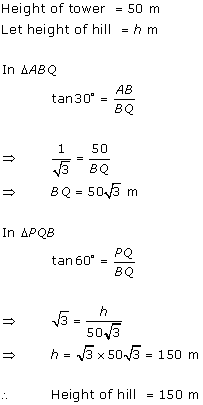
Solution 56 (i)
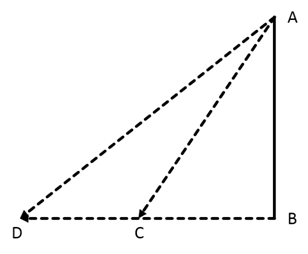
Let AB be the cliff, so AB=150m.
C and D are positions of the boat.
DC is the distance covered in 2 min.
∠ACB = 60o and ∠ADB = 45o
∠ABC = 90o
In ΔABC,
tan(∠ACB)= ![]()
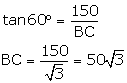
In ΔABD,
tan(∠ADB)= ![]()
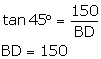
So, DC=BD - BC
=![]()
Now,
Solution 56 (ii)
Let AB be the lighthouse and C be the position of man initially.
Suppose, a man changes his position from C to D.
As per the question, we obtain the following figure
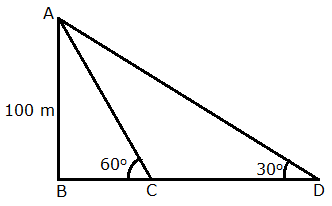
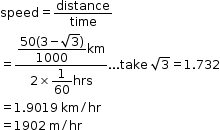
Let speed of the boat be x metres per minute.
Therefore, CD = 2x
Using trigonometry, we have
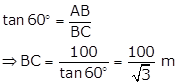
Also,
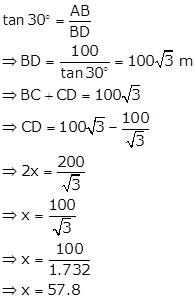
Hence, speed of the boat is 57.8 m.
Solution 57
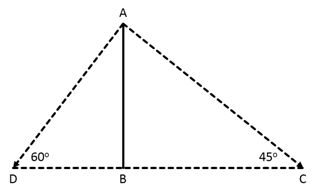
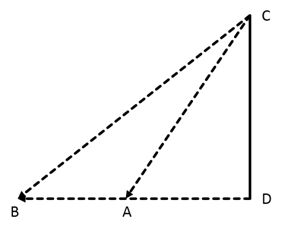
AB is the tower.
DC is the distance between cars.
AB=120m
In ΔABC,
tan(∠ACB) = ![]()
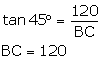
In ΔABD,
tan(∠ADB) = ![]()
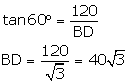
So, DC=BD+BC
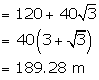
Solution 58
Let CD be the tower.
So CD =15m
AB is the distance between the points.
∠CAD = 60o and ∠CBD = 45o
∠ADC = 90o
In ΔADC,
tan(∠CAD)= ![]()
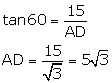
In ΔCBD,
tan(∠CBD)= ![]()
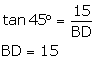
So AB=BD - AD
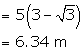
Solution 59
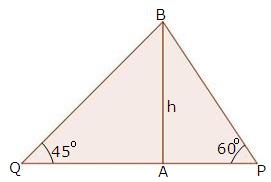
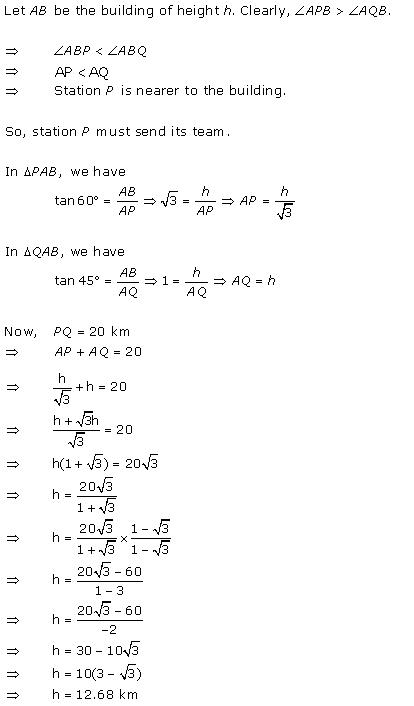
Now,
in triangle APB,
sin 60o = AB/ BP
√3/2 = h/ BP
This gives
h = 14.64 km
Solution 60
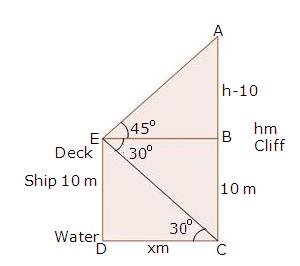

Solution 61
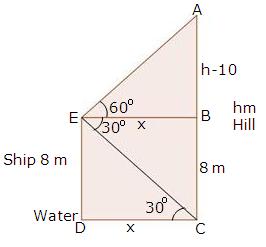

Solution 62
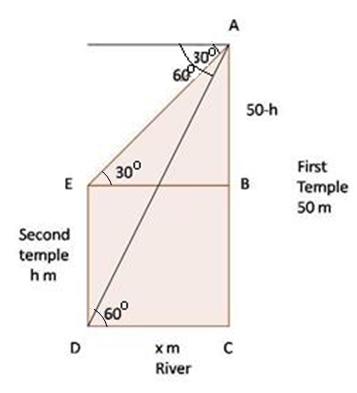
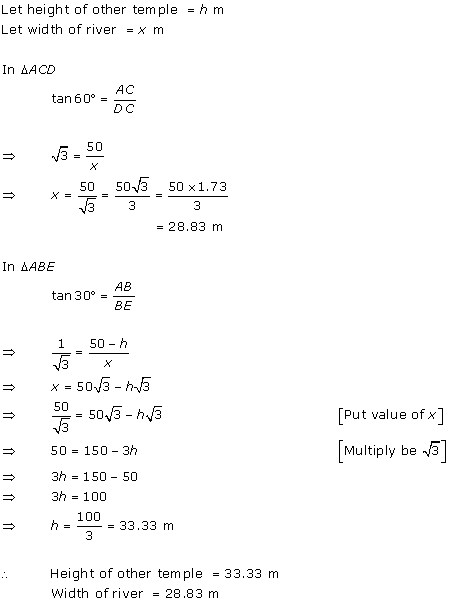
Solution 63
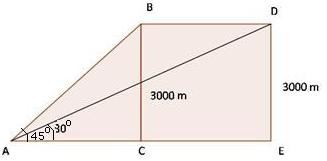

Solution 64
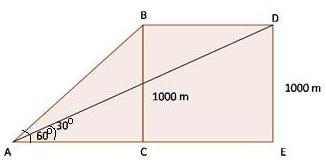

Solution 65
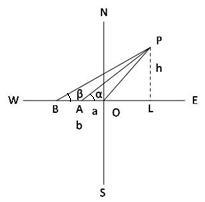

Solution 66
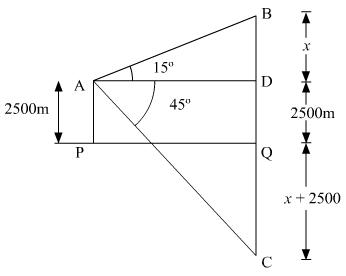

Solution 67
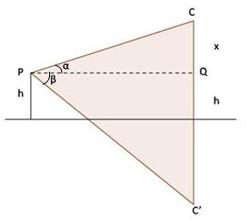
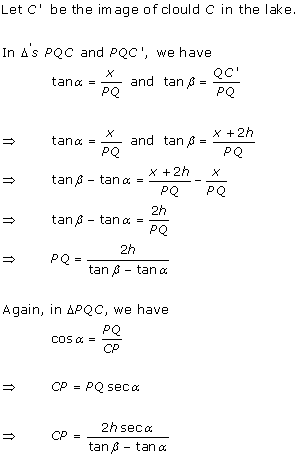
Solution 68
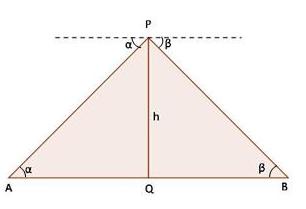

Solution 69
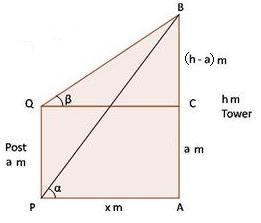
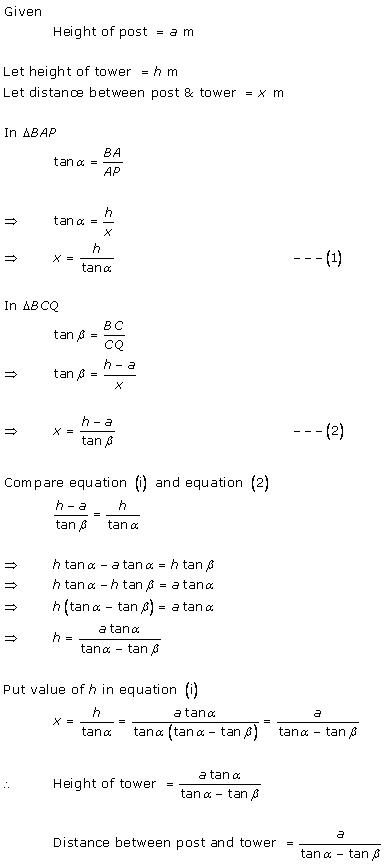
Solution 70
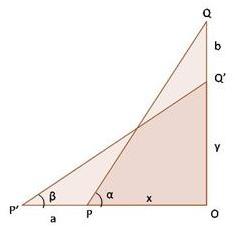

Solution 71
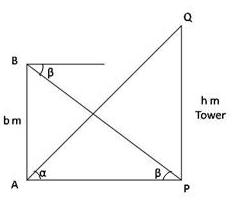

Solution 72
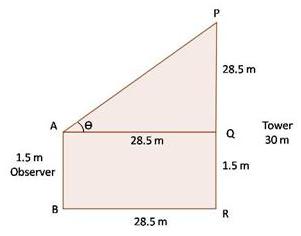

Solution 73
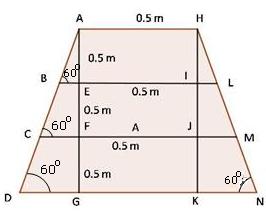

Solution 74
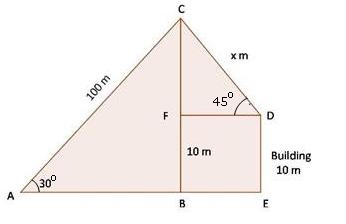
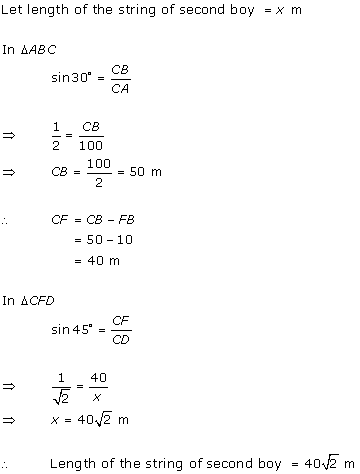
Solution 75
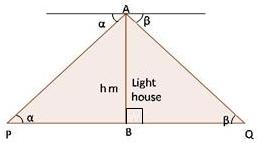

Solution 76

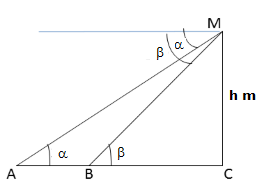

Solution 77
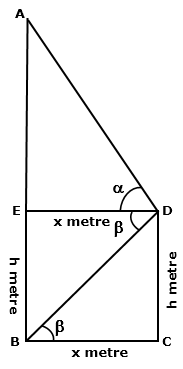

Solution 78
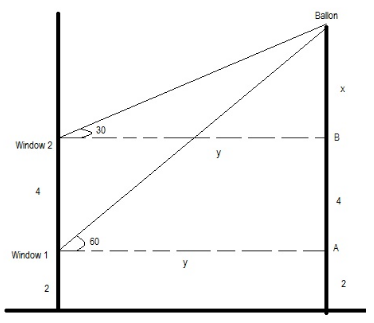
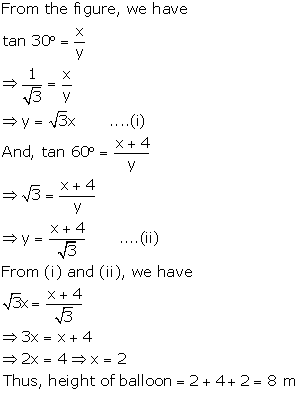
Some Applications of Trigonometry Exercise 12.41
Solution 1
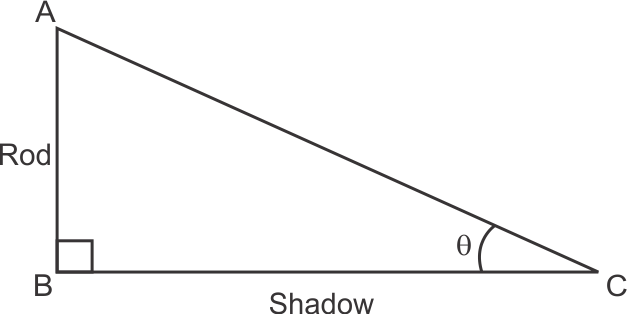

Solution 2


Solution 3
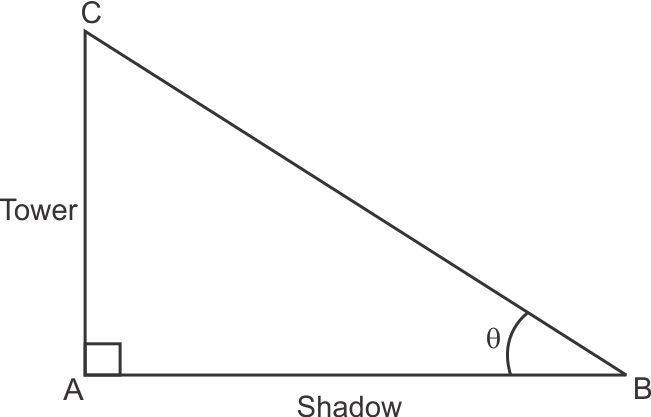

Solution 4
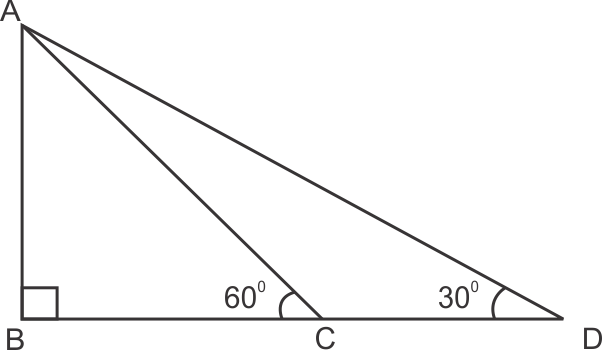

Solution 5
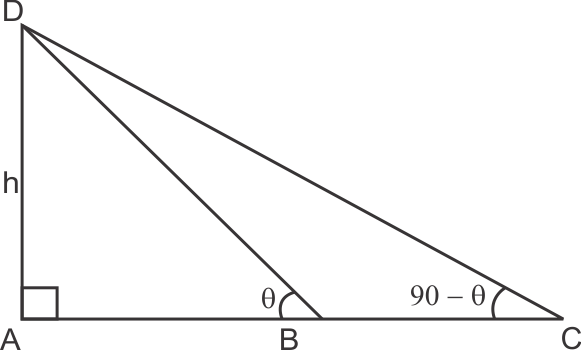
Solution 6

Solution 7

Solution 8
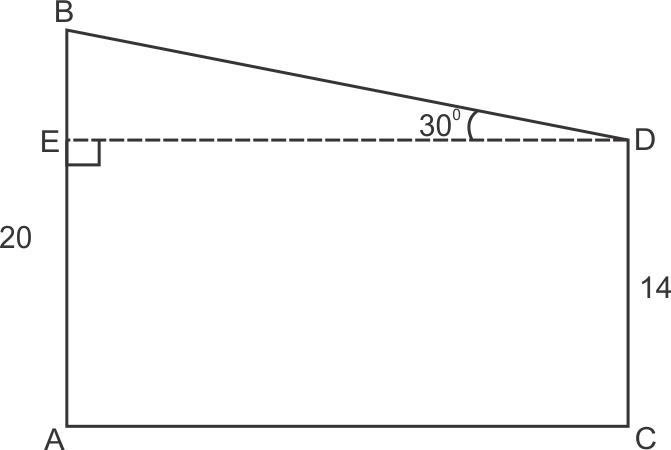
Wire BD
ED || AC
So, EA = DC and ED = AC
EA = 14
AB = EA + EB
20 = 14 + EB
EB = 6
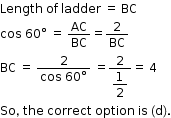
So, the correct option is (a).
Solution 9

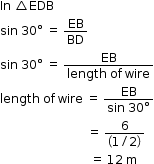
Solution 10
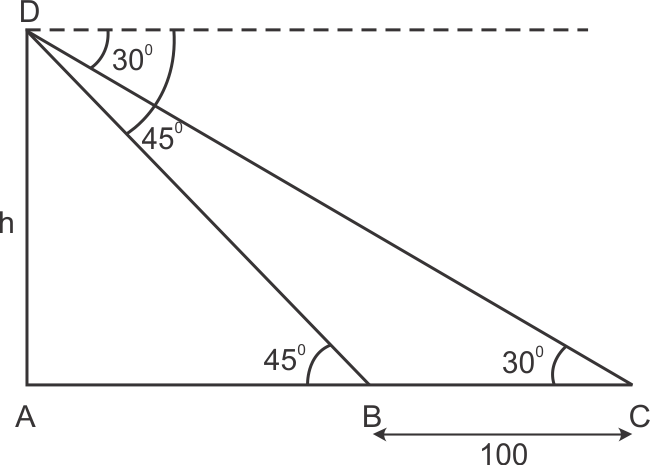
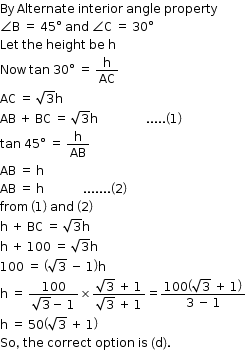
Some Applications of Trigonometry Exercise 12.42
Solution 11
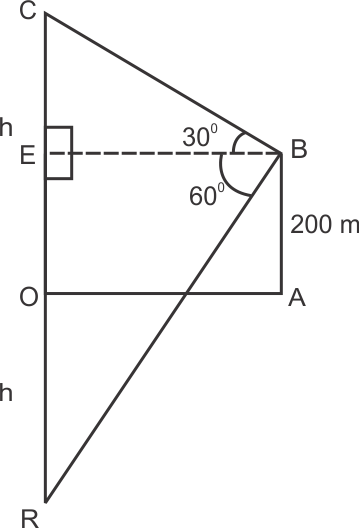

Solution 12
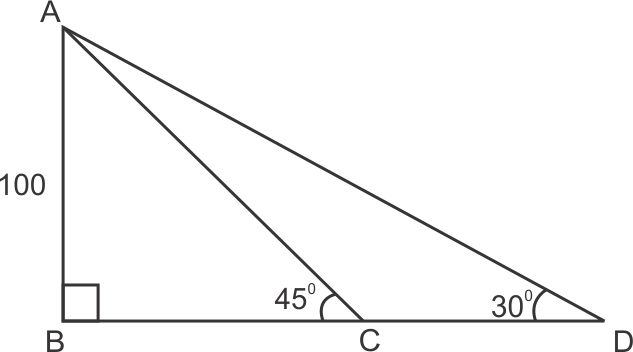

Solution 13
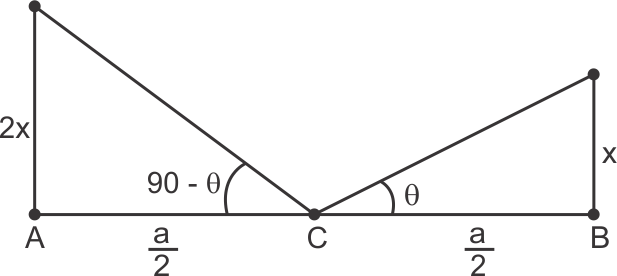
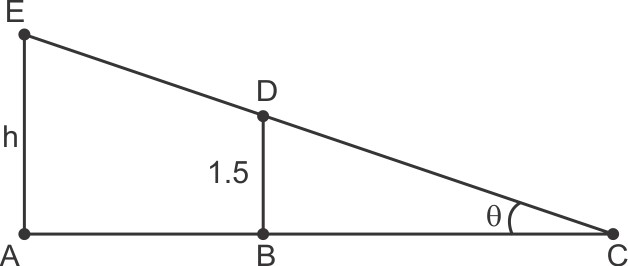
If height of one person is x then height of another one is 2x. Also If angle of elevation of one is θ then for another it is 90 - θ.
AB = a
C is mid point.
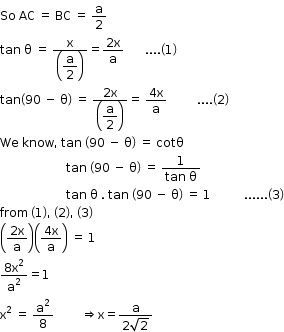
So, the correct option is (d).
Solution 14
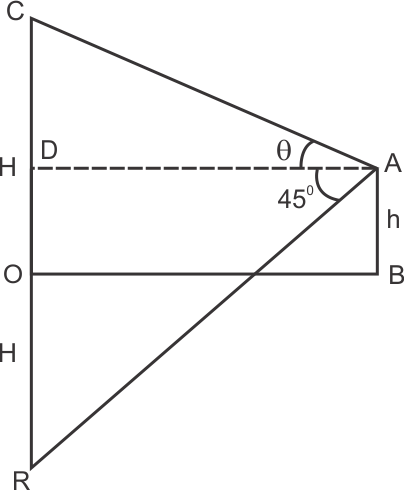

Solution 15
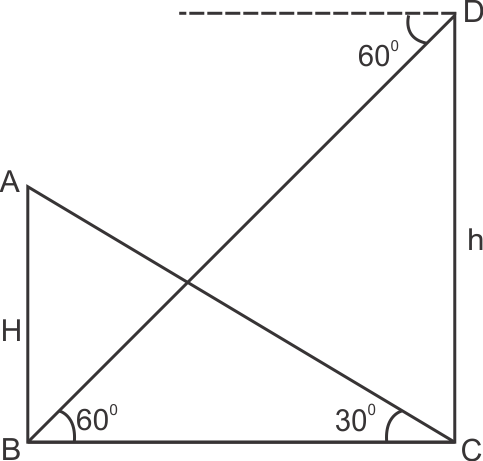

Solution 16
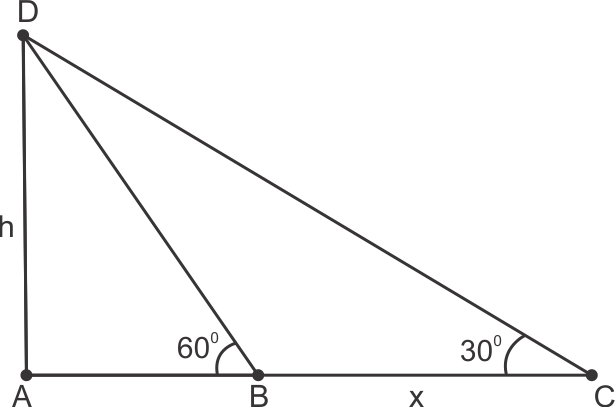
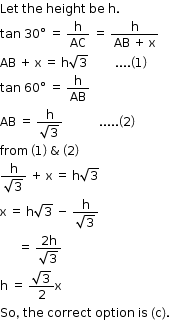
Solution 17
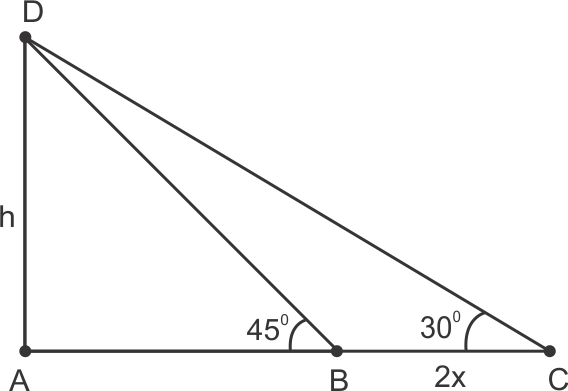
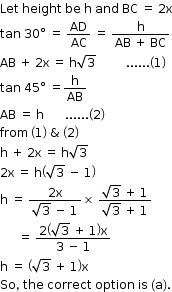
Solution 18
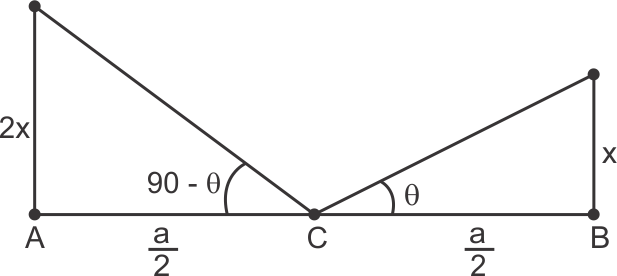
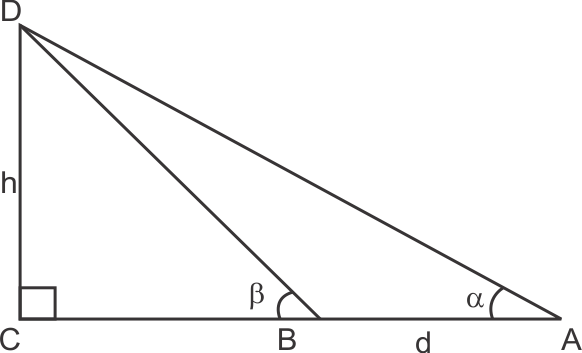
If height of one pole is x then height of the other one is 2x. Also If the angle of elevation of one is θ then for the other it is
90 - θ.
AB = a
C is mid point.
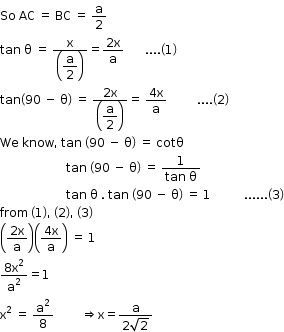
So, the correct option is (b).
Solution 19
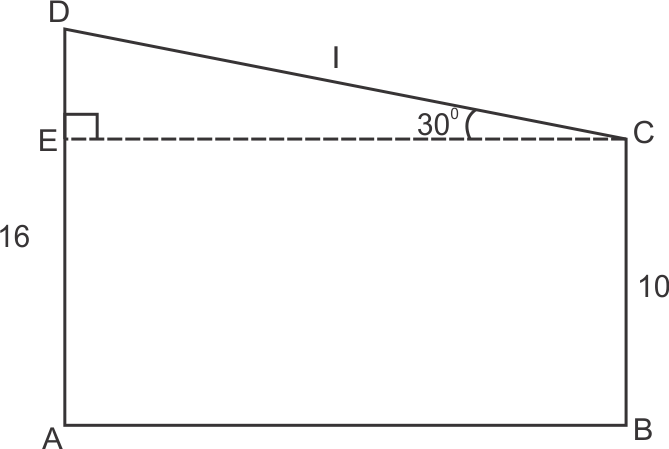
EC || AB
Hence
EA = CB = 10
AD = AE + ED
ED = AD - AE
= 16 - 10 = 6
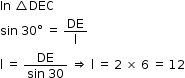
So, the correct option is (c).
Solution 20

Some Applications of Trigonometry Exercise 12.43
Solution 21
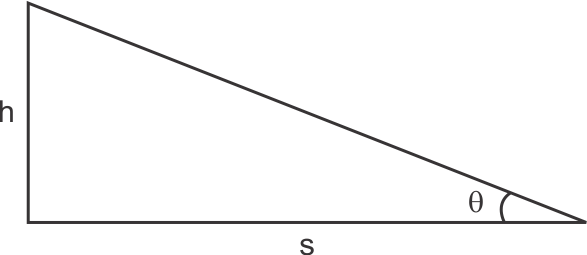

Solution 22
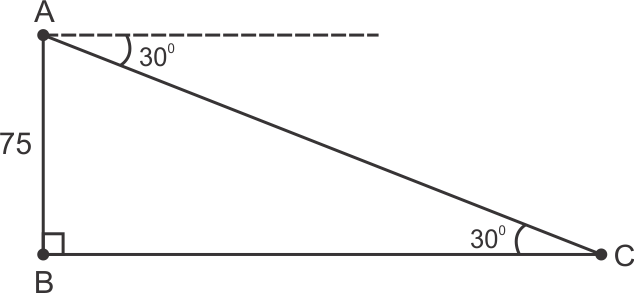
From the figure, it is cleared that we have to find the length of BC.

Solution 23
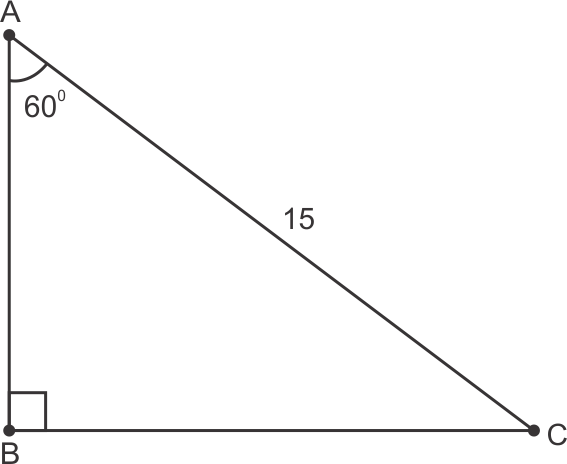
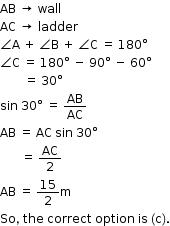
Solution 24
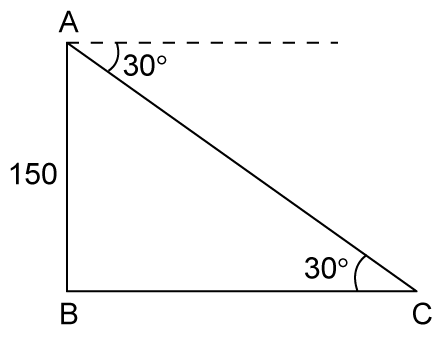

Solution 25

Solution 26
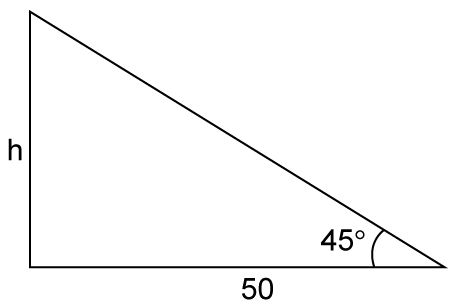
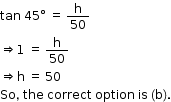
Solution 27