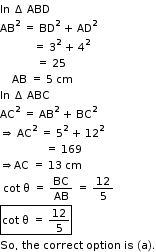Chapter 10 Trigonometric Ratios
Class 10th R. D. Sharma Maths Solution
CBSE Class 10 Maths
R. D. Sharma Solution
Trigonometric Ratios Exercise Ex. 10.1
Solution 1 (i)

Solution 1 (ii)

Solution 1 (iii)
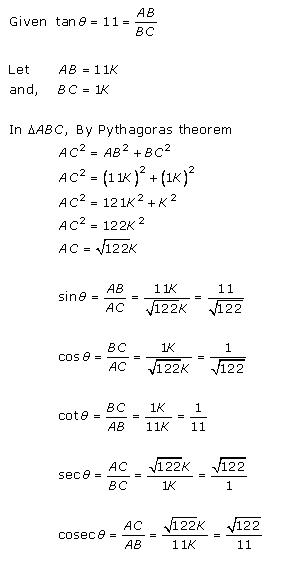
Solution 1 (iv)
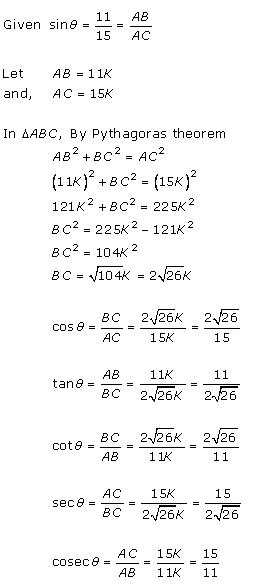
Solution 1 (v)

Solution 1 (vi)
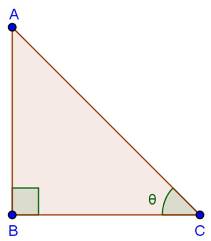
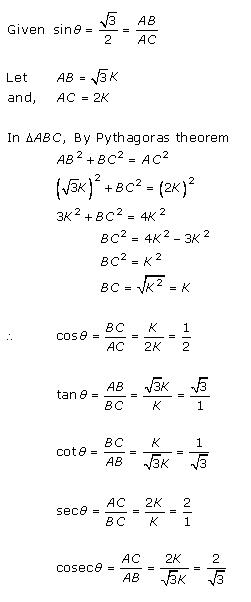
Solution 1 (vii)
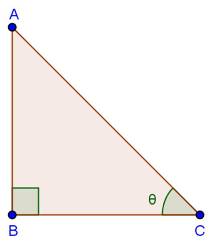

Solution 1 (viii)
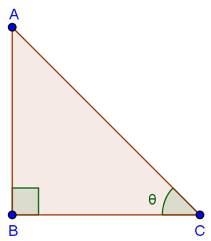

Solution 1 (ix)

Solution 1 (x)

Solution 1 (xi)

Solution 1 (xii)

Solution 2
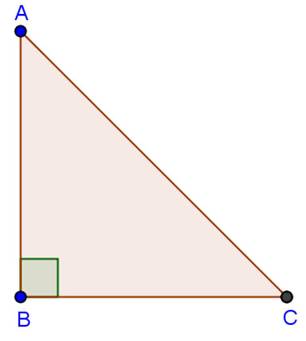
In ![]() ABC
by applying Pythagoras theorem
ABC
by applying Pythagoras theorem
AC2 = AB2 +
BC2
= (24)2 + (7)2
= 576 + 49
=
625
AC =
= 25 cm

Solution 3
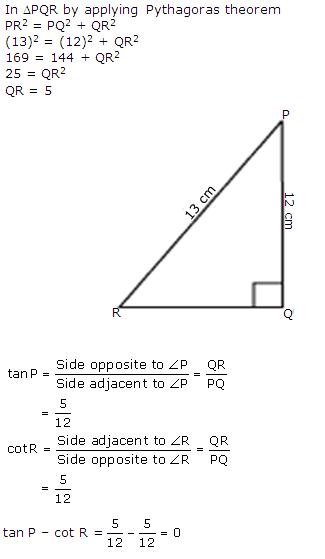
Solution 4

Solution 5
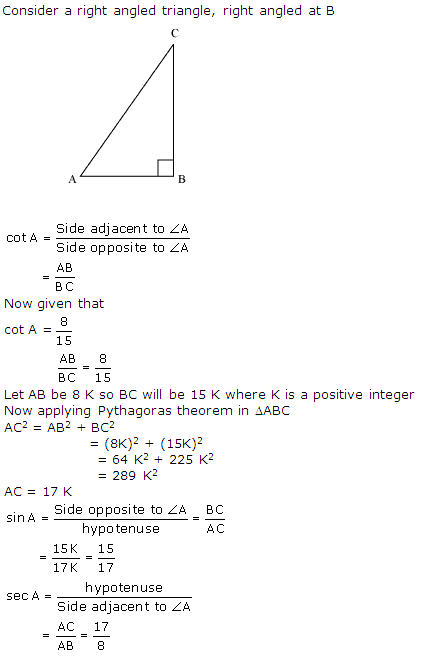
Solution 6
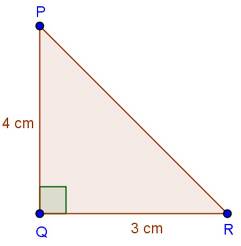

Solution 7
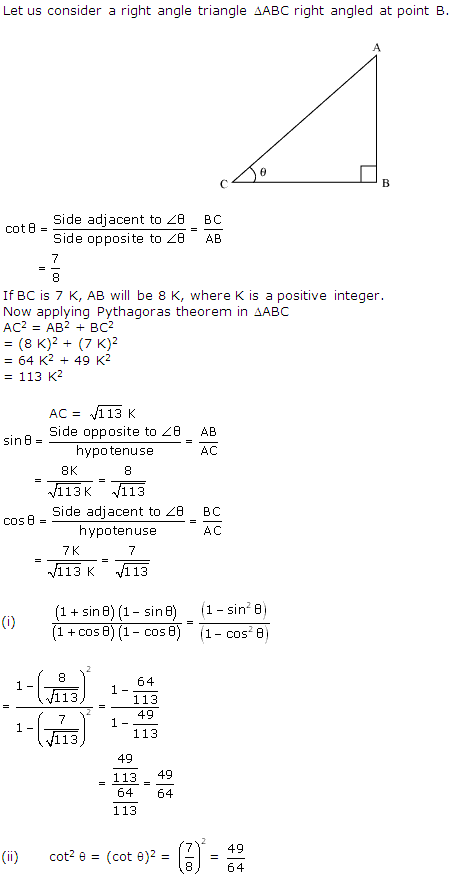
Solution 8

Solution 9
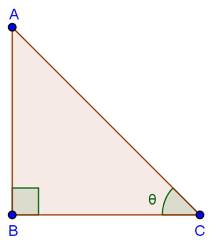

Solution 10
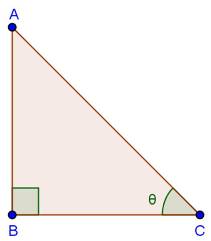
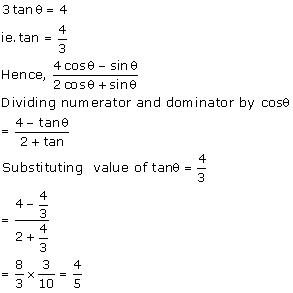
Solution 11
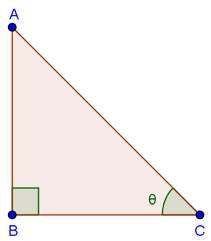

Solution 12
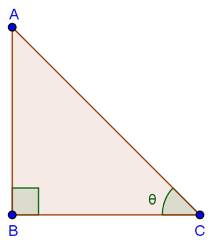

Solution 13
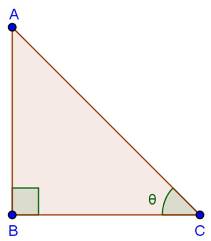
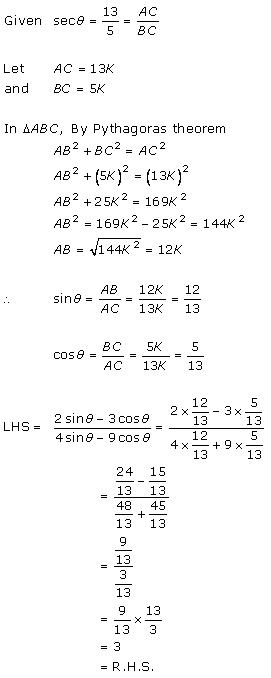
Solution 14

Solution 15

Solution 16

Solution 17

Solution 18
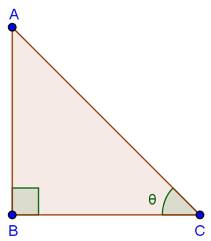

Solution 19
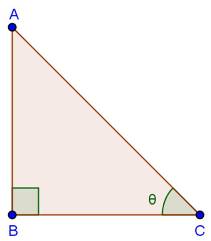

Solution 20
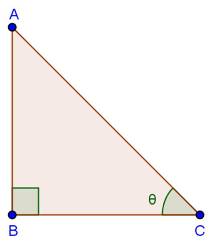

Solution 21
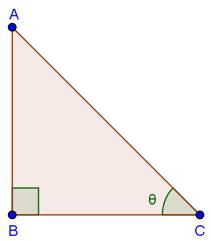

Solution 22

Solution 23
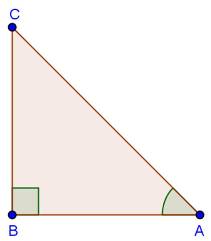

Solution 24
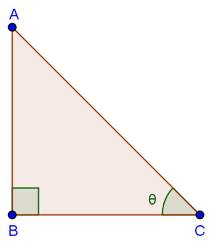

Solution 26
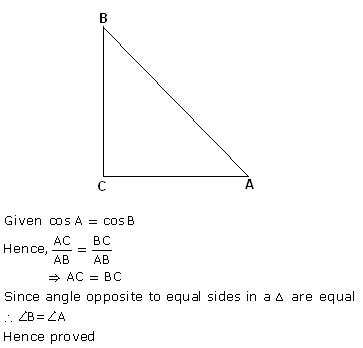
Solution 27
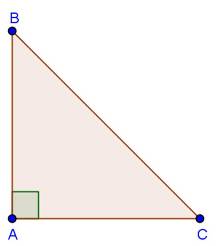

Solution 28

Solution 29

Solution 30

Solution 31

Solution 32

Solution 33


Solution 34

Solution 35

Solution 36

Solution 25
Given: ![]()
![]()
![]()
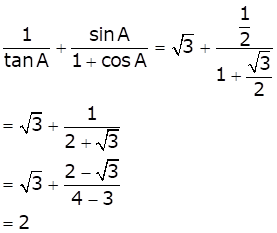
Trigonometric Ratios Exercise Ex. 10.2
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Solution 17
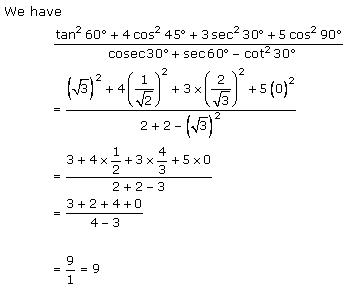
Solution 18

Solution 19

Solution 20

Solution 21

Solution 22

Solution 23

Solution 24
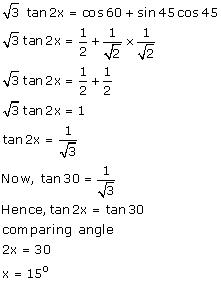
Solution 25

Solution 26 (i)

Solution 26 (ii)

Solution 26 (iii)

Solution 26 (iv)

Solution 27 (i)

Solution 27 (ii)

Solution 27 (iii)

Solution 28 (i)

Solution 28 (ii)

Solution 29

Solution 30 (i)
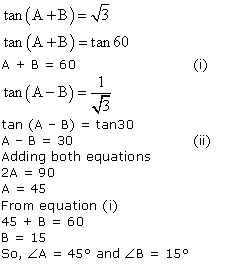
Solution 31
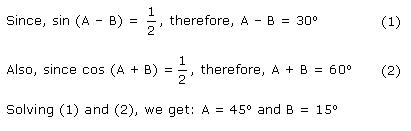
Solution 32

Solution 33

Solution 34
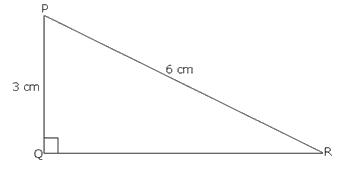

Solution 35

Solution 36
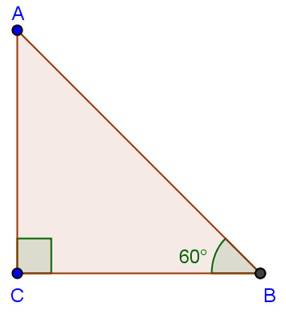

Solution 37
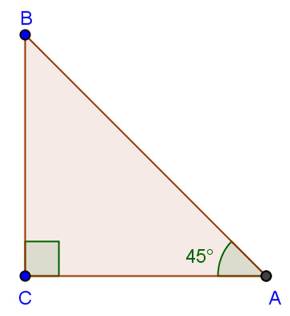
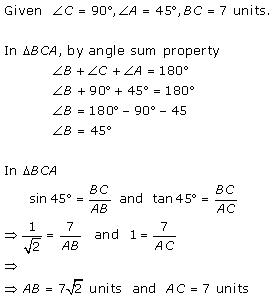
Solution 38
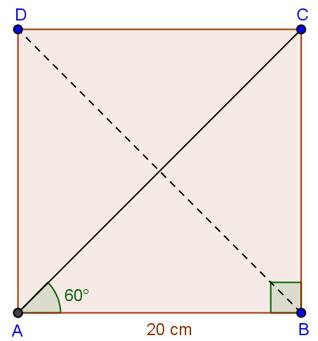
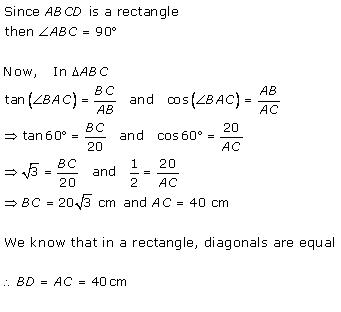
Solution 39

Solution 40

Solution 30 (ii)
Given: tan(A + B) = 1 and ![]()
Therefore,
A + B = 45o … (i)
A - B = 30o … (ii)
Adding the two equations, we get
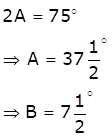
Trigonometric Ratios Exercise Ex. 10.3
Solution 1

Solution 2 (i)
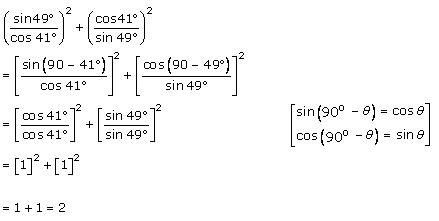
Solution 2 (ii)

Solution 2 (iii)
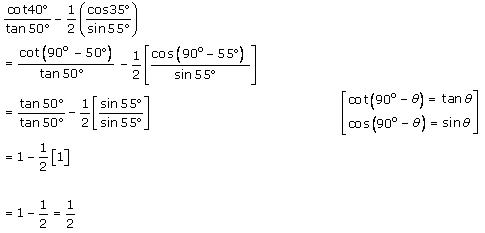
Solution 2 (iv)
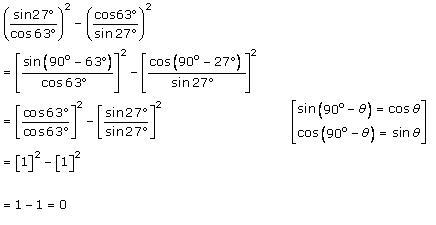
Solution 2 (v)

Solution 2 (vi)
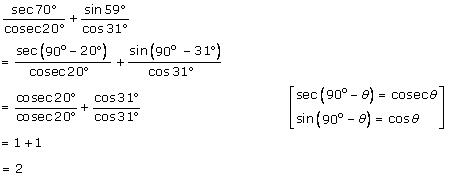
Solution 2 (vii)
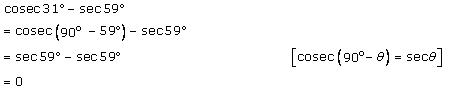
Solution 2 (viii)

Solution 2 (ix)

Solution 2 (x)
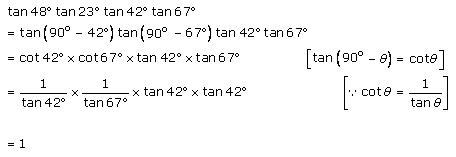
Solution 2 (xi)
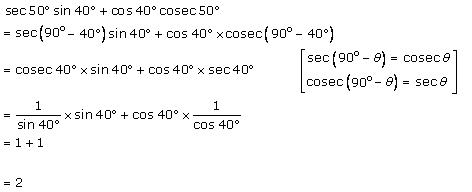
Solution 3
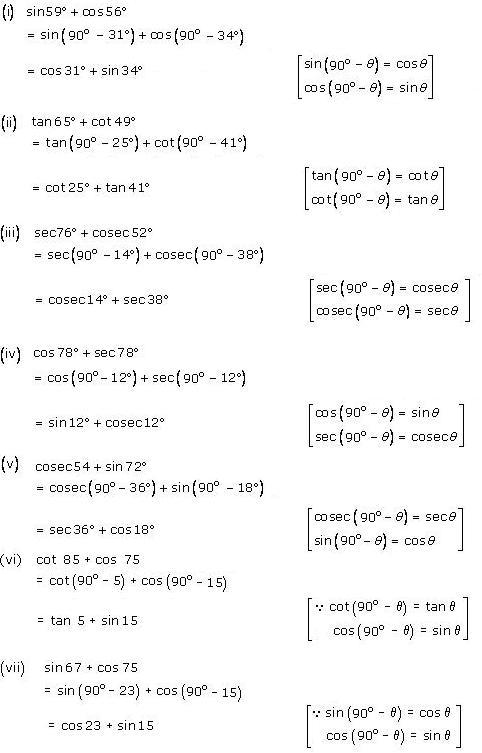
Solution 4
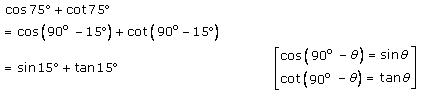
Solution 5
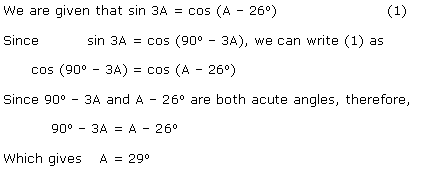
Solution 6(i)
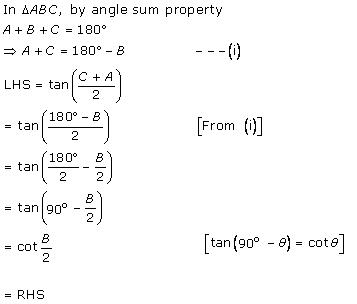
Solution 6(ii)
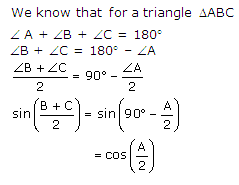
Solution 7 (i)
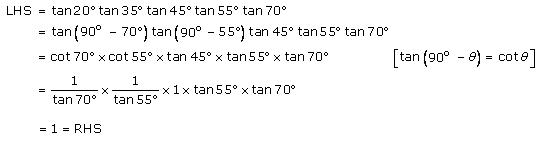
Solution 7 (ii)
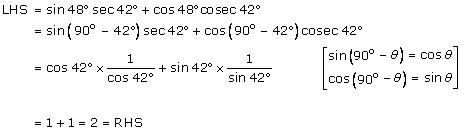
Solution 7 (iii)
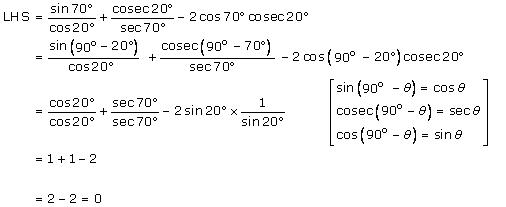
Solution 7 (iv)
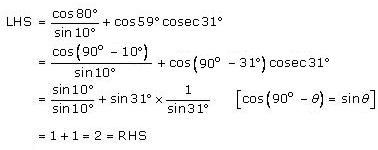
Solution 8 (i)
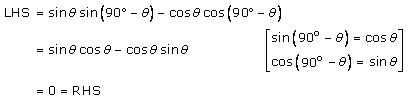
Solution 8 (ii)

Solution 8 (iii)
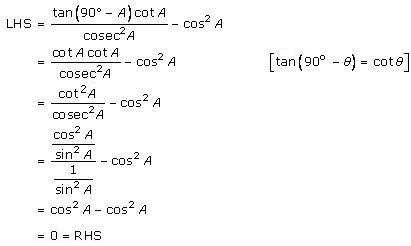
Solution 8 (iv)
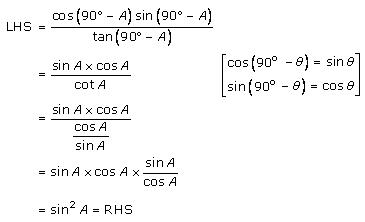
Solution 8 (v)

Solution 9 (i)

Solution 9 (ii)

Solution 9 (iii)
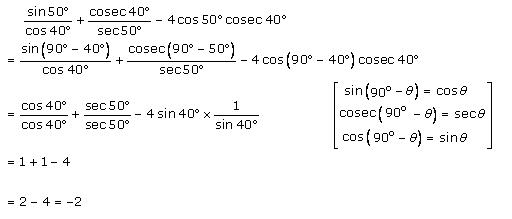
Solution 9 (iv)
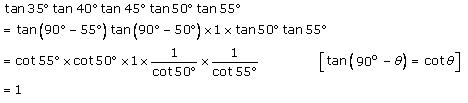
Solution 9 (v)

Solution 9 (vi)
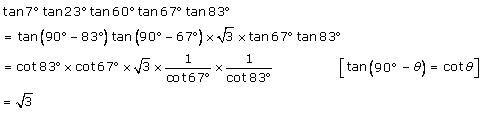
Solution 9 (vii)

Solution 9 (viii)

Solution 9 (ix)

Solution 9 (x)

Solution 10
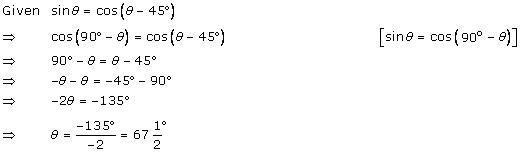
Solution 11 (ii)
Solution 12
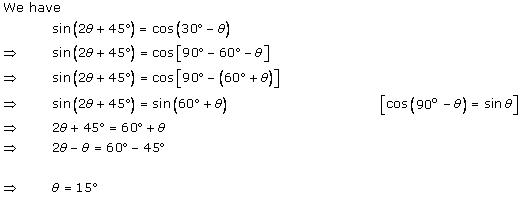
Solution 13
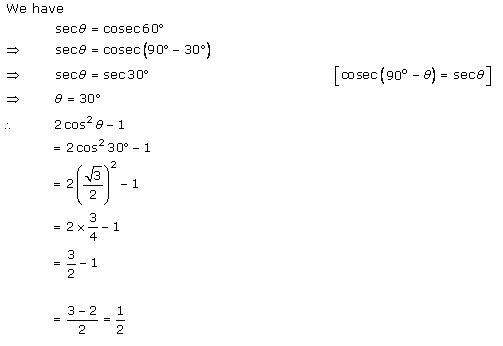
Solution 14
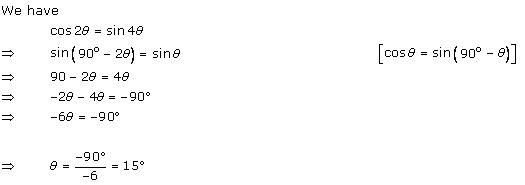
Solution 15
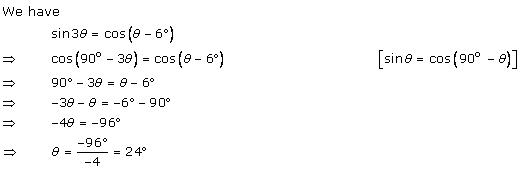
Solution 16
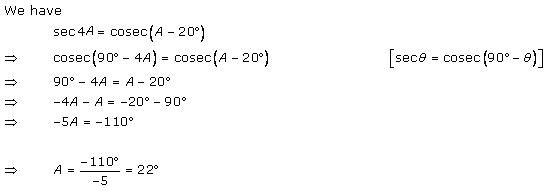
Solution 17
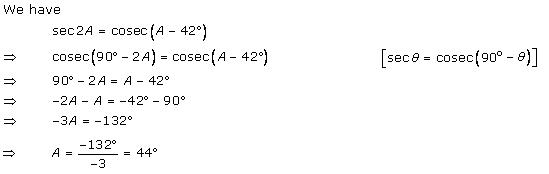
Solution 6 (iii)
Given: ∠A = 90o
For a triangle ABC, ∠A + ∠B + ∠C = 90o
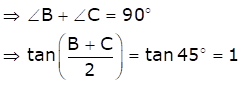
Solution 9 (xi)
Using the identities
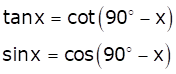
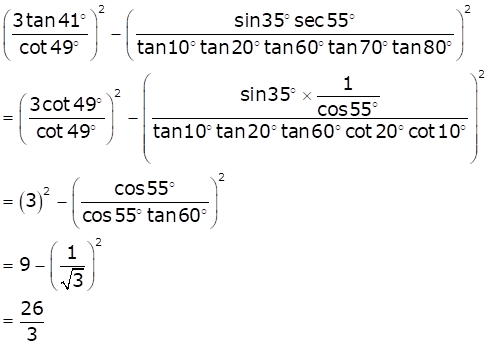
Solution 11 (i)
For a triangle ABC, ∠A + ∠B + ∠C = 90o
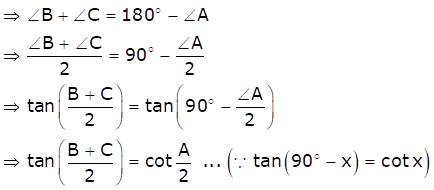
Solution 18
Given: tan 2A = cot(A - 18o)
As tan x = cot(90o - x), we have
cot(90o - 2A) = cot(A - 18o)
90o - 2A = A - 18o
3A = 108o
Therefore, A = 36o.
Trigonometric Ratios Exercise 10.56
Solution 1

Solution 2
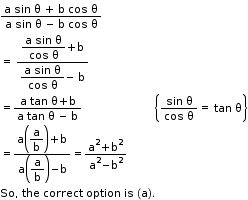
Solution 3
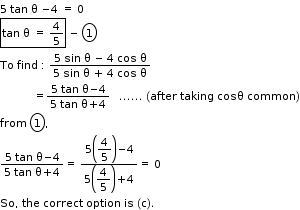
Solution 4
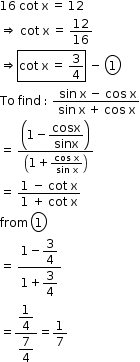
So, the correct option is (a).
Solution 5
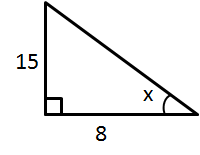
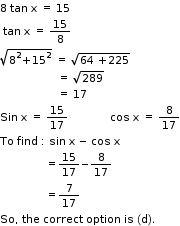
Solution 6
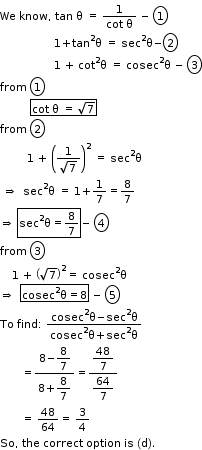
Trigonometric Ratios Exercise 10.57
Solution 7
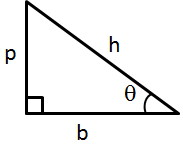
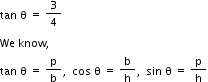
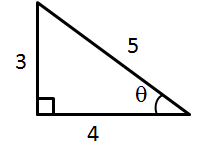

Solution 8

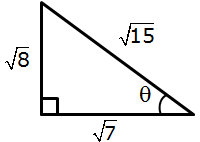
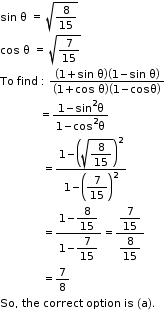
Solution 9

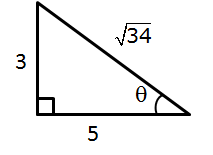
Solution 10
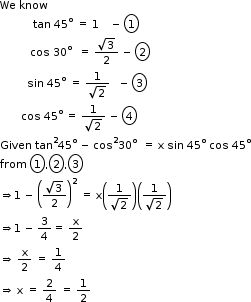
So, the correct option is (d).
Solution 11
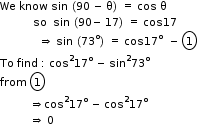
So, the correct option is (c).
Solution 12

Solution 13
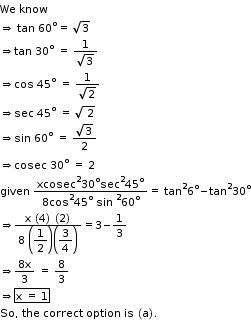
Solution 14

Solution 15
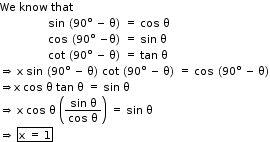
So, the correct option is (b).
Solution 16
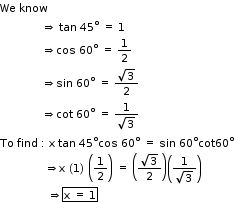
So, the correct option is (a).
Solution 17
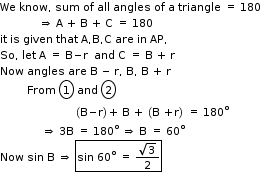
So, the correct option is (b).
Solution 18
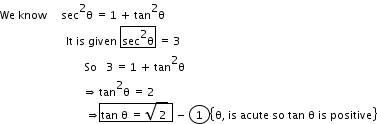
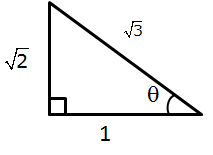
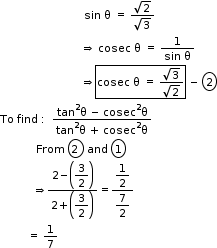
So, the correct option is (d).
Trigonometric Ratios Exercise 10.58
Solution 19

Solution 20
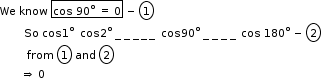
So, the correct option is (b).
Solution 21

Solution 22

Solution 23

Solution 24

Solution 25

Solution 26
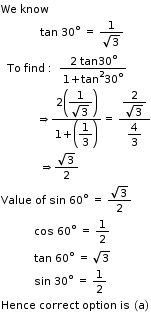
Solution 27
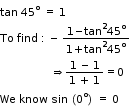
So, the correct option is (d).
Solution 28

So, the correct option is (a).
Solution 29
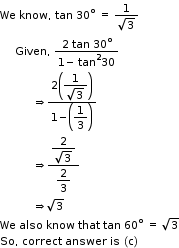
Solution 30

Solution 31
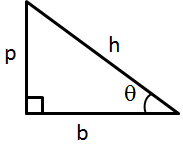
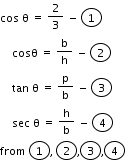
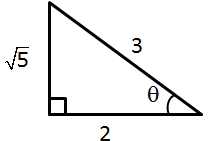
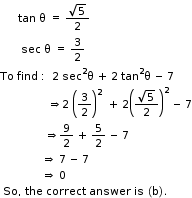
Solution 32
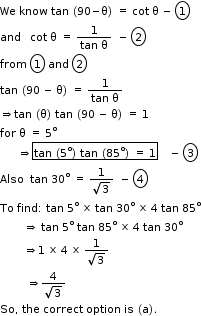
Trigonometric Ratios Exercise 10.59
Solution 33

So, the correct option is (c).
Solution 34
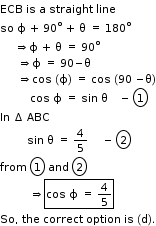
Solution 35