Chapter 1: Real Numbers
Class 10th R. D. Sharma Maths Solution
CBSE Class 10 Maths
R. D. Sharma Solution
Real Numbers Exercise Ex. 1.1
Solution 1
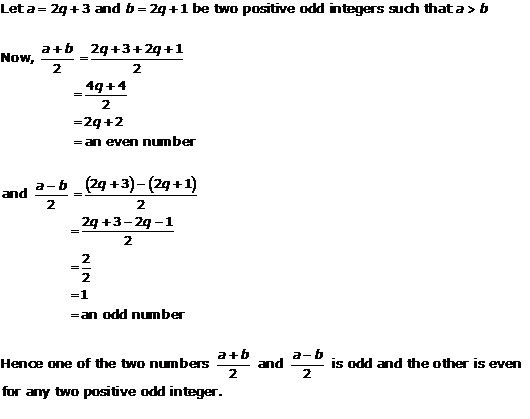
Solution 2
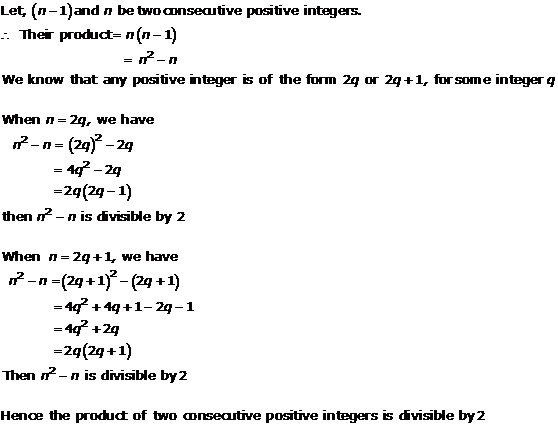
Solution 3

Solution 4

Solution 5

Solution 6

Solution 7
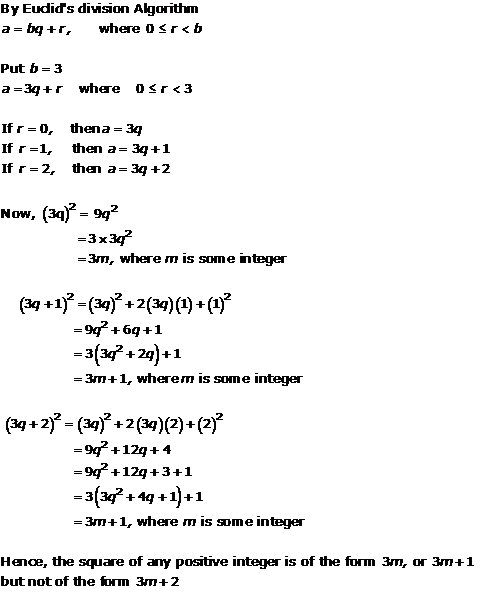
Solution 8

Solution 9

Solution 10
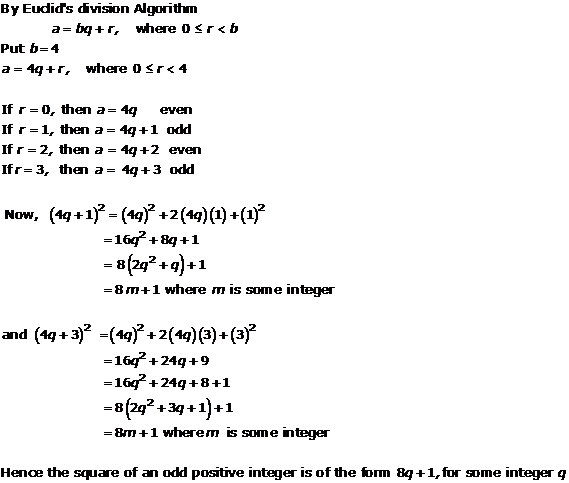
Solution 11
Let a
be any odd positive integer we need to prove that a is of the form 6q+1 ,
or 6q+3 , or 6q+5 , where q is some
integer.
Since a is an integer consider b = 6 another
integer applying Euclid's division lemma we get
a =
6q + r f or some integer q ![]() 0, and r = 0, 1, 2, 3, 4, 5 since
0, and r = 0, 1, 2, 3, 4, 5 since
0 ![]() r < 6.
r < 6.
Therefore, a = 6q or 6q + 1 or 6q + 2 or 6q + 3 or
6q + 4 or 6q + 5
However since a is odd so a cannot take the
values 6q, 6q+2 and 6q+4
(since all these are divisible by
2)
Also, 6q + 1 = 2 x 3q + 1 = 2k1 + 1, where k1 is a
positive integer
6q + 3 = (6q + 2) + 1 = 2 (3q + 1) + 1 =
2k2 + 1, where k2 is an integer
6q + 5 = (6q + 4) + 1 = 2
(3q + 2) + 1 = 2k3 + 1, where k3 is an
integer
Clearly, 6q + 1, 6q + 3, 6q + 5 are of the form 2k +
1, where k is an integer.
Therefore, 6q + 1, 6q + 3, 6q + 5
are odd numbers.
Therefore, any odd integer can be
expressed is of the form
6q + 1, or 6q + 3, or 6q + 5 where
q is some integer
Concept Insight: In order to
solve such problems Euclid's division lemma is applied to two integers a
and b the integer b must be taken in accordance with what is to be proved, for
example here the integer b was taken 6 because a must be of the form 6q +
1, 6q + 3, 6q + 5.
Basic definition of even (divisible
by 2) and odd numbers (not divisible by 2) and the fact that addition and
multiplication of integers is always an integer are applicable
here.
Solution 12
Let the three consecutive positive integers be m, (m + 1) and (m + 2).
By Euclid's division lemma, when m is divided by 3, we have
m = 3q + r for some integer q ≥ 0 and r = 0, 1, 2
Case 1: When m = 3q
In this case, clearly, m is divisible by 3.
But, (m + 1) and (m + 2) are not divisible by 3.
Case 2: When m = 3q + 1
In this case, m + 2 = 3(q + 1), which is divisible by 3.
But, m and (m + 1) are not divisible by 3.
Case 3: When m = 3q + 2
In this case, m + 1 = 3(q + 1), which is divisible by 3.
But, m and (m + 2) are not divisible by 3.
Hence, one of m, (m + 1) and (m + 2) is always divisible by 3.
Solution 13
Let x be any positive integer.
When we divide x by 6, the remainder is either 0 or 1 or 2 or 3 or 4 or 5.
So, x can be written as
x = 6a or x = 6a + 1 or x = 6a + 2 or x = 6a + 3 or x = 6a + 4 or x = 6a + 5.
Thus, we have the following cases:
CASE I:
When x = 6a,
x2 = 36a2 = 6(6a2) = 6m, where m = 6a2
CASE II:
When x = 6a + 1,
x2 = (6a + 1)2 = 36a2 + 12a + 1 = 6(6a2 + 2a) + 1 = 6m + 1, where m = 6a2 + 2a
CASE III:
When x = 6a + 2,
x2 = (6a + 2)2 = 36a2 + 24a + 4 = 6(6a2 + 4a) + 4 = 6m + 4, where m = 6a2 + 4a
CASE IV:
When x = 6a + 3,
x2 = (6a + 3)2 = 36a2 + 36a + 9 = (36a2 + 36a + 6) + 3 = 6(6a2 + 6a + 1) + 3 = 6m + 3, where m = 6a2 + 6a + 1
CASE V:
When x = 6a + 4,
x2 = (6a + 4)2 = 36a2 + 48a + 16 = (36a2 + 48a + 6) + 10 = 6(6a2 + 8a + 1) + 10 = 6m + 10, where m = 6a2 + 8a + 10
CASE VI:
When x = 6a + 5,
x2 = (6a + 5)2 = 36a2 + 60a + 25 = (36a2 + 60a + 6) + 19 = 6(6a2 + 10a + 1) + 19 = 6m + 19, where m = 6a2 + 10a + 19
Here, x is of the form 6m or 6m + 1 or 6m + 3 or 6m + 4 or 6m + 10 or 6mn + 19.
So, it cannot be of the form 6m + 2 or 6m + 5.
Solution 14
Let x be any positive integer.
Then, it is of the form 6n, 6n + 1, 6n + 2, 6n + 3, 6n + 4 or 6n + 5.
So, we have the following cases:
CASE I:
When x = 6n,
x3 = (6n)3 = 216n3 = 6(36n3) = 6q, where q = 36n3
CASE II:
When x = 6n + 1,
x3 = (6n + 1)3 = 216n3 + 108n2 + 18n + 1 = 6(36n3 + 18n2 + 3n) + 1 = 6q + 1, where q = 36n3 + 18n2 + 3n
CASE III:
When x = 6n + 2,
x3 = (6n + 2)3 = 216n3 + 216n2 + 72n + 8 = 216n3 + 216n2 + 72n + 6 + 2 =6(36n3 + 36n2 + 12n + 1) + 2 = 6q + 2, where q = 36n3 + 54n2 + 12n + 1
CASE IV:
When x = 6n + 3,
x3 = (6n + 3)3 = 216n3 + 324n2 + 162n + 27 = 216n3 + 324n2 + 162n + 24 + 3 =6(36n3 + 54n2 + 27n + 4) + 3 = 6q + 3, where q = 36n3 + 54n2 + 27n + 4
CASE V:
When x = 6n + 4,
x3 = (6n + 4)3 = 216n3 + 432n2 + 288n2 + 64 = 216n3 + 432n2 + 288n + 60 + 4 =6(36n3 + 72n2 + 48n + 10) + 4 = 6q + 4, where q = 36n3 + 72n2 + 48n + 10
CASE VI:
When x = 6n + 5,
x3 = (6n + 5)3 = 216n3 + 540n2 + 450n2 + 125 = 216n3 + 540n2 + 450n + 120 + 5 =6(36n3 + 90n2 + 75n + 20) + 5 = 6q + 5, where q = 36n3 + 72n2 + 48n + 10
Thus, the cube of any positive integer is of the form 6q + r, where q is an integer and r = 0, 1, 2, 3, 4, 5.
Solution 15
Given numbers are n, n + 4, n + 8, n + 12 and n + 16.
Let n = 5q + r, where 0 ≤ r < 5
n = 5q, 5q + 1, 5q + 2, 5q + 3 or 5q + 4 for any natural number q.
So, we have the following cases:
CASE I:
When n = 5q
n = 5q is divisible by 5
n + 4 = 5q + 4 is not divisible by 5
n + 8 = 5q + 8 = 5q + 5 + 3 = 5(q + 1) + 3 is not divisible by 5
n + 12 = 5q + 12 = 5q + 10 + 2 = 5(q + 2) + 2 is not divisible by 5
n + 16 = 5q + 16 = 5q + 15 + 1 = 5(q + 3) + 1 is not divisible by 5
CASE II:
When n = 5q + 1
n = 5q + 1 is not divisible by 5
n + 4 = 5q + 1 + 4 = 5q + 5 = 5(q + 1) is divisible by 5
n + 8 = 5q + 1 + 8 = 5q + 9 = 5q + 5 + 4 = 5(q + 1) + 4 is not divisible by 5
n + 12 = 5q + 1 + 12 = 5q + 13 = 5q + 10 + 3 = 5(q + 2) + 3 is not divisible by 5
n + 16 = 5q + 1 + 16 = 5q + 17 = 5q + 15 + 2 = 5(q + 3) + 2 is not divisible by 5
CASE III:
When n = 5q + 2
n = 5q + 2 is not divisible by 5
n + 4 = 5q + 2 + 4 = 5q + 6 = 5q + 5 + 1 = 5(q + 1) + 1 is not divisible by 5
n + 8 = 5q + 2 + 8 = 5q + 10 = 5(q + 2) is divisible by 5
n + 12 = 5q + 2 + 12 = 5q + 14 = 5q + 10 + 4 = 5(q + 2) + 4 is not divisible by 5
n + 16 = 5q + 2 + 16 = 5q + 18 = 5q + 15 + 3 = 5(q + 3) + 3 is not divisible by 5
CASE IV:
When n = 5q + 3
n = 5q + 3 is not divisible by 5
n + 4 = 5q + 3 + 4 = 5q + 7 = 5q + 5 + 2 = 5(q + 1) + 2 is not divisible by 5
n + 8 = 5q + 3 + 8 = 5q + 11 = 5(q + 2) + 1 is not divisible by 5
n + 12 = 5q + 3 + 12 = 5q + 15 = 5(q + 3) is divisible by 5
n + 16 = 5q + 3 + 16 = 5q + 19 = 5q + 15 + 4 = 5(q + 3) + 4 is not divisible by 5
CASE V:
When n = 5q + 4
n = 5q + 4 is not divisible by 5
n + 4 = 5q + 4 + 4 = 5q + 8 = 5q + 5 + 3 = 5(q + 1) + 3 is not divisible by 5
n + 8 = 5q + 4 + 8 = 5q + 12 = 5(q + 2) + 2 is not divisible by 5
n + 12 = 5q + 4 + 12 = 5q + 16 = 5q + 15 + 1 = 5(q + 3) + 1 is not divisible by 5
n + 16 = 5q + 4 + 16 = 5q + 20 = 5(q + 4) is divisible by 5
Hence, in each case, one and only one out of n, n + 4, , n + 8, n + 12 and n + 16 is divisible by 5.
Solution 16
We know that any positive integer can be of the form 6m, 6m + 1, 6m + 2, 6m + 3, 6m + 4 or 6m + 5 for some integer m.
Thus, an odd positive integer x can be of the form 6m + 1, 6m + 3 or 6m + 5.
Thus, we have
CASE I:
x = 6m + 1
x2 = (6m + 1)2 = 36m2 + 12m + 1 = 6(6m2 + 2m) + 1 = 6q + 1, where q = 6m2 + 2m
CASE II:
x = 6m + 3
x2 = (6m + 3)2 = 36m2 + 36m + 9 = 36m2 + 36m + 6 + 3 = 6(6m2 + 6m + 1) + 3 = 6q + 3, where q = 6m2 + 6m + 1
CASE III:
x = 6m + 5
x2 = (6m + 5)2 = 36m2 + 60m + 25 = 36m2 + 60m + 24 + 1 = 6(6m2 + 10m + 4) + 1 = 6q + 1, where q = 6m2 + 10m + 4
Thus, the square of an odd positive integer can be of the form 6q + 1 or 6q + 3.
Solution 17
By Euclid's Lemma,
a = bq + r, 0 ≤ r < b
Here, a is any positive integer and b = 3,
a = 3q + r
So, this must be in the form 3q, 3q + 1 or 3q + 2.
Now,
(3q)2 = 9q2 = 3m
(3q + 1)2 = 9q2 + 6q + 1 = 3(3q2 + 2q) + 1 = 3m + 1
(3q + 2)2 = 9q2 + 12q + 4 = 9q2 + 12q + 3 + 1 = 3(3q2 + 4q + 1) + 1 = 3m + 1
Thus, square of a positive integer of the form 3q + 1 is always of the form 3m + 1 or 3m for some integer m.
Solution 18
Let x be any positive integer.
So, x can be written as
x = 3a or x = 3a + 1 or x = 3a + 2
Thus, we have the following cases:
CASE I:
When x = 3a,
x2 = 9a2 = 3(3a2) = 3m, where m = 3a2
CASE II:
When x = 3a + 1,
x2 = (3a + 1)2 = 9a2 + 6a + 1 = 3(3a2 + 2a) + 1 = 3m + 1, where m = 3a2 + 2a
CASE III:
When x = 3a + 2,
x2 = (3a + 2)2 = 9a2 + 12a + 4 = 9a2 + 12a + 3 + 1 = 3(3a2 + 4a + 1) + 1 = 3m + 1, where m = 3a2 + 4a + 1
Thus, the square of any positive integer cannot be of the form 3m + 2, where m is a natural number.
Real Numbers Exercise Ex. 1.2
Solution 1(i)

Solution 1(ii)

Solution 1(iii)

Solution 1(iv)

Solution 1(v)

Solution 1(vi)
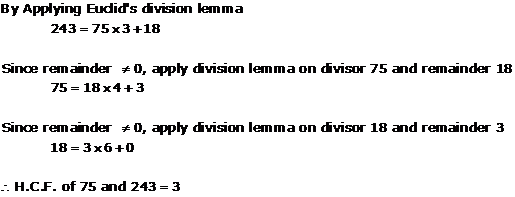
Solution 1(vii)
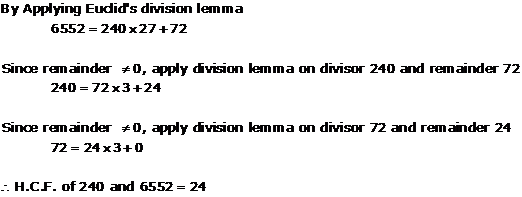
Solution 1(viii)

Solution 1(ix)

Solution 1(x)

Solution 2(i)
135 and 225
Step 1: Since 225 > 135, apply Euclid's division lemma, to a =225 and b=135 to find q and r such that 225 = 135q+r, 0 r
On dividing 225 by 135 we get quotient as 1 and remainder as 90
i.e 225 =
135 x 1 + 90
Step 2: Remainder r which is 90 0, we apply Euclid's division lemma to a =
135 and b = 90 to find whole numbers q and r such that
135 = 90 x q + r 0
r<90
On dividing 135 by 90 we get quotient as 1 and remainder as 45
i.e
135 = 90 x 1 + 45
Step 3: Again remainder r = 45 0 so we apply Euclid's division lemma to a =
90 and b = 45 to find q and r such that
90 = 45 x q + r 0 r<45
On
dividing 90 by 45 we get quotient as 2 and remainder as 0
i.e 90 = 2 x 45 +
0
Step 4: Since the remainder is zero, the divisor at this stage will be HCF of (135, 225).
Since the divisor at this stage is 45, therefore, the HCF of 135 and 225 is 45.
Solution 2(ii)
196 and 38220
Step 1: Since 38220 > 196, apply Euclid's division lemma
to a =38220
and b=196 to find whole numbers q and r such that
38220 = 196 q + r, 0 r
< 196
On dividing 38220 we get quotient as 195 and remainder r as 0
i.e 38220 = 196 x 195 + 0
Since the remainder is zero, divisor at this
stage will be HCF
Since divisor at this stage is 196 , therefore, HCF of 196
and 38220 is 196.
NOTE: HCF( a,b) = a if a is a factor of b. Here, 196 is a factor of 38220 so
HCF is 196.
Solution 2(iii)
867 and 255
Step 1: Since 867 > 255, apply Euclid's division lemma, to a =867 and
b=255 to find q and r such that 867 = 255q + r, 0 r<255
On dividing 867 by
255 we get quotient as 3 and remainder as 102
i.e 867 = 255 x 3 + 102
Step 2: Since remainder 102 0, we apply the division lemma to a=255 and b=
102 to find whole numbers q and r such that
255 = 102q + r where 0
r<102
On dividing 255 by 102 we get quotient as 2 and remainder as 51
i.e 255 = 102 x 2 + 51
Step 3: Again remainder 51 is non zero, so we apply the division lemma to
a=102 and b= 51 to find whole numbers q and r such that
102 = 51 q + r where
0 r < 51
On dividing 102 by 51 quotient is 2 and remainder is
0
i.e 102 = 51 x 2 + 0
Since the remainder is zero, the divisor at this
stage is the HCF
Since the divisor at this stage is 51,therefore, HCF of 867
and 255 is 51.
Concept Insight: To crack such problem remember to apply the Euclid's division Lemma which states that "Given positive integers a and b, there exists unique integers q and r satisfying a = bq + r, where 0 r < b" in the correct order.
Here, a > b.
Euclid's algorithm works since Dividing 'a' by 'b', replacing 'b' by 'r' and 'a' by 'b' and repeating the process of division till remainder 0 is reached, gives a number which divides a and b exactly.
i.e HCF(a,b) =HCF(b,r)
Note that do not find the HCF using prime factorisation in this question when the method is specified and do not skip steps.
lemma to a=135 and b=
Solution 2(iv)
![]()

Solution 2(v)

Solution 2(vi)
Step 1: Since 7344 > 1260, apply Euclid's division lemma, to a = 7344 and b = 1260 to find q and r such that 7344 = 1260q + r, 0 ≤ r < 1260
On dividing 7344 by 1260 we get quotient as 5 and remainder as
i.e. 7344 = 1260 x 5 + 1044
Step 2: Remainder r which is 1044, we apply Euclid's division lemma to a = 1260 and b = 1044 to find whole numbers q and r such that
1260 = 1044 x q + r, 0 ≤ r < 1044
On dividing 1260 by 1044 we get quotient as 1 and remainder as 216
i.e. 1260 = 1044 x 1 + 216
Step 3: Again remainder r = 216, so we apply Euclid's division lemma to a = 1044 and b = 216 to find q and r such that
1044 = 216 x q + r, 0 ≤ r < 216
On dividing 1044 by 216 we get quotient as 4 and remainder as 180
i.e. 1044 = 216 x 4 + 180
Step 4: Again remainder r = 180, so we apply Euclid's division lemma to a = 216 and b = 180 to find q and r such that
216 = 180 x q + r, 0 ≤ r < 180
On dividing 216 by 180 we get quotient as 1 and remainder as 36
i.e. 216 = 180 x 1 + 36
Step 5: Again remainder r = 36, so we apply Euclid's division lemma to a = 180 and b = 36 to find q and r such that
180 = 36 x q + r, 0 ≤ r < 36
On dividing 180 by 36 we get quotient as 5 and remainder as 0
i.e. 180 = 36 x 5 + 0
Step 6: Since the remainder is zero, the divisor at this stage will be HCF of (7344, 1260).
Since the divisor at this stage is 36, therefore, the HCF of 7344 and 1260 is 36.
Solution 2(vii)
Step 1: Since 2048 > 960, apply Euclid's division lemma, to a = 2048 and b = 960 to find q and r such that 2048 = 960q + r, 0 ≤ r < 960
On dividing 2048 by 960 we get quotient as 5 and remainder as
i.e. 2048 = 960 x 2 + 128
Step 2: Remainder r which is 128, we apply Euclid's division lemma to a = 960 and b = 128 to find whole numbers q and r such that
960 = 128 x q + r, 0 ≤ r < 128
On dividing 960 by 128 we get quotient as 7 and remainder as 216
i.e. 960 = 128 x 7 + 64
Step 3: Again remainder r = 64, so we apply Euclid's division lemma to a = 128 and b = 64 to find q and r such that
128 = 64 x q + r, 0 ≤ r < 64
On dividing 128 by 64 we get quotient as 2 and remainder as 0
i.e. 128 = 64 x 2 + 0
Step 4: Since the remainder is zero, the divisor at this stage will be HCF of (2048, 960).
Since the divisor at this stage is 64, therefore, the HCF of 2048 and 960 is 64.
Solution 3(i)

Solution 3(ii)

Solution 3(iii)
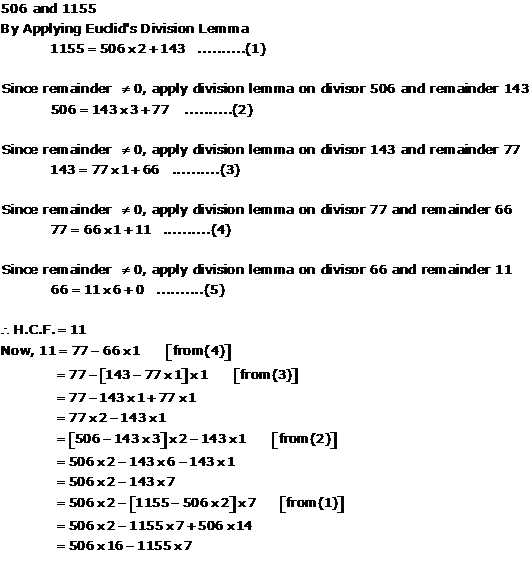
Solution 3(iv)
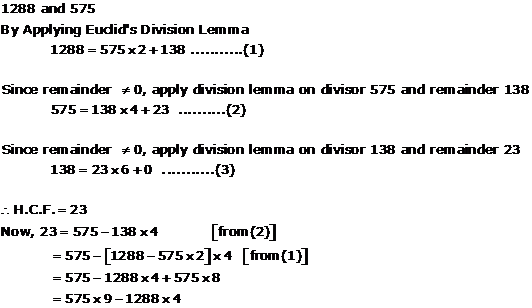
Solution 4

Solution 5
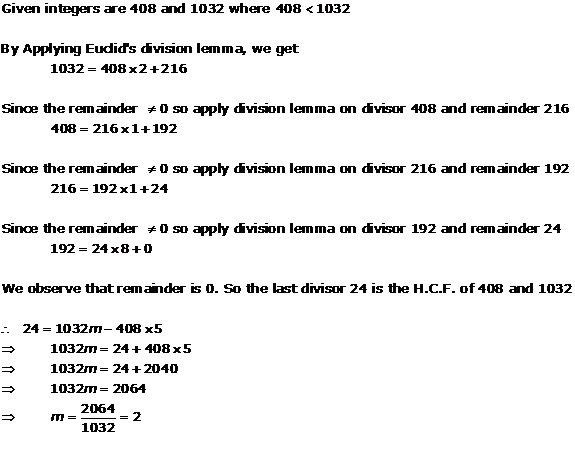
Solution 6
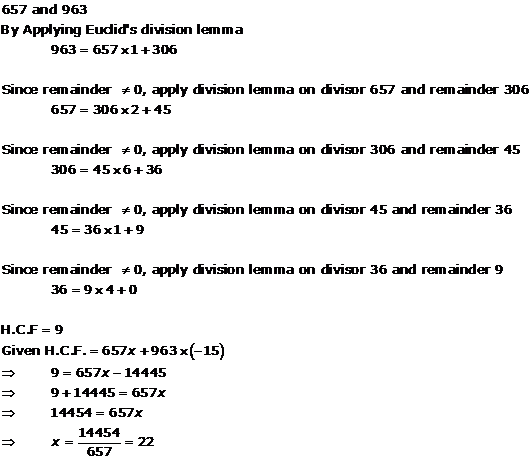
Solution 7
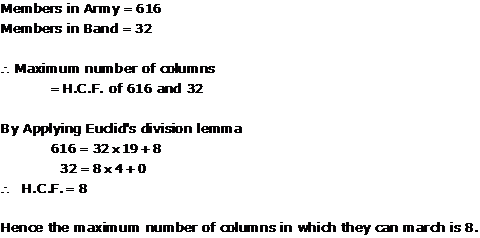
Solution 8

Solution 9
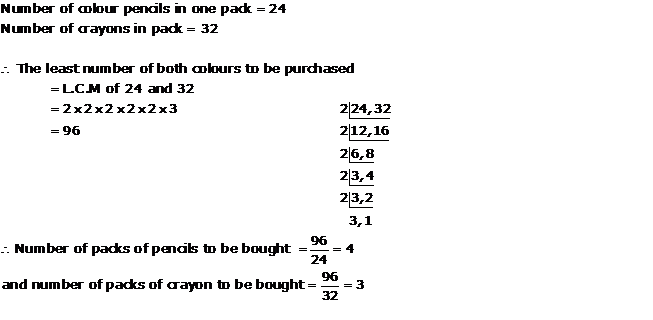
Solution 10
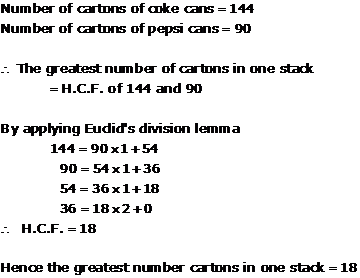
Solution 11
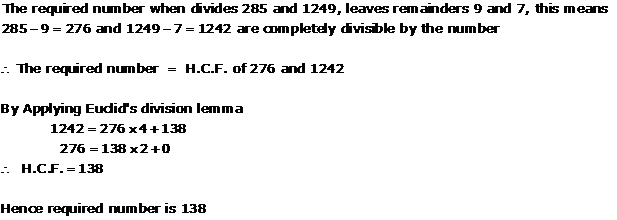
Solution 12

Solution 13
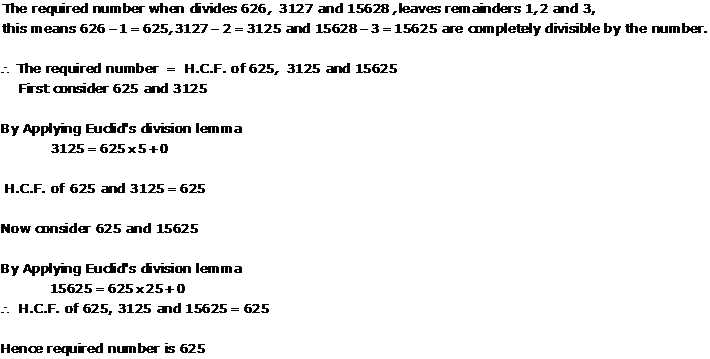
Solution 14
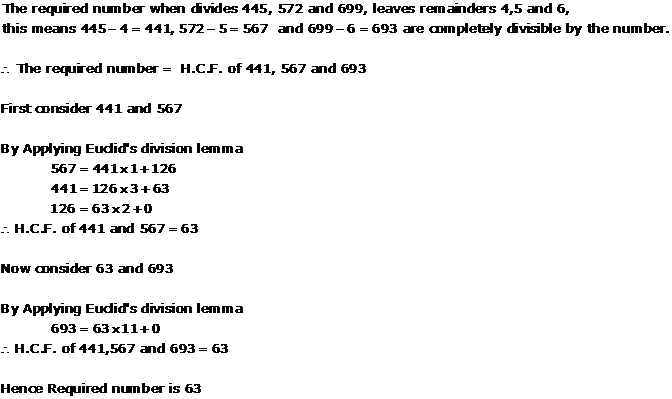
Solution 15

Solution 16

Solution 17
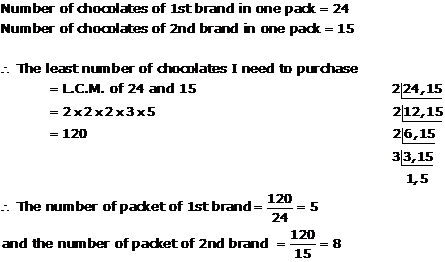
Solution 18
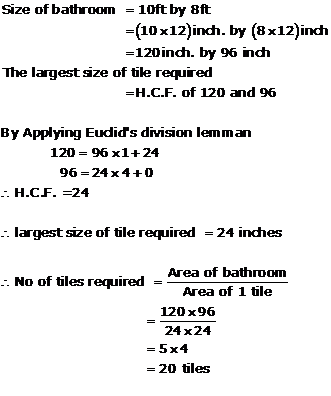
Solution 19
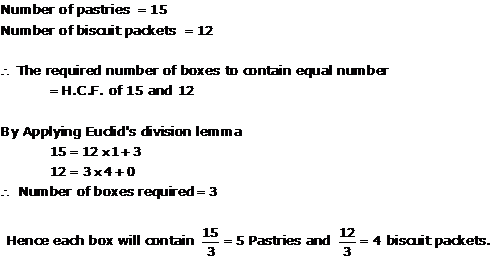
Solution 20
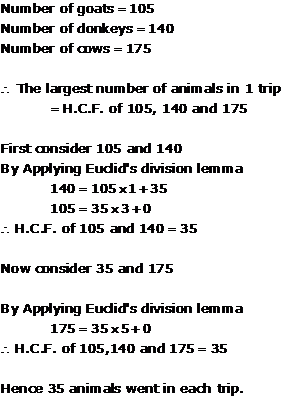
Solution 21

Solution 22
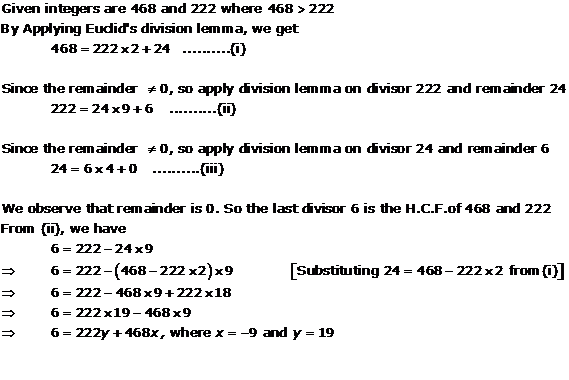
Real Numbers Exercise Ex. 1.3
Solution 1

Solution 2

Solution 3
It can be observed that
7 x 11 x 13 + 13 = 13 x (7 x 11 + 1) = 13 x (77 + 1)
= 13 x 78
= 13 x 13 x 6
The given expression has 6 and 13 as its factors. Therefore, it is a composite number.
7 x 6 x 5 x 4 x 3 x 2 x 1 + 5 = 5 x (7 x 6 x 4 x 3 x 2 x 1 + 1)
= 5 x (1008 + 1)
= 5 x 1009
1009 cannot be factorised further. Therefore, the given expression has 5 and 1009 as its factors. Hence, it is a composite number.
Concept Insight: Definition of prime numbers and composite numbers is used. Do not miss the reasoning.
Solution 4
Prime factorisation of 6n = (2 x 3)n
By Fundamental Theorem of Arithmetic Prime factorisation of a number is unique. So 5 is not a prime factor of 6n.
Hence, for any value of n, 6n will not be divisible by 5.
Therefore, 6n cannot end with the digit 0 for any natural number n.
Concept Insight: In order solve such problems the concept used is if a number is to end with zero then it must be divisible by 10 and the prime factorisation of a number is unique.
Solution 5
Numbers are of two types - prime and composite. Prime numbers has only two factors namely 1 and the number itself whereas composite numbers have factors other than 1 and itself. It can be observed that 3 × 5 × 7+ 7 = 7 × (3 × 5 + 1) = 7 × (15 + 1) = 7 × 16
The given expression has 7 and 16 as its factors. Therefore, it is a composite number.
Real Numbers Exercise Ex. 1.4
Solution 1
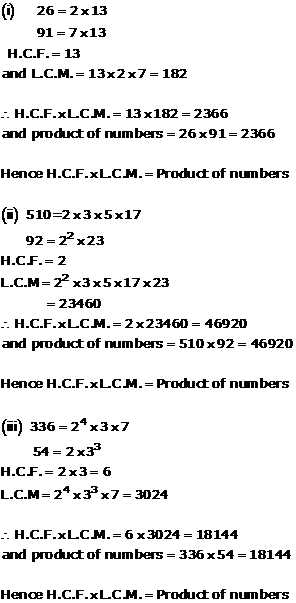
Solution 1(iv)
404 = 2 × 2 × 3 × 37 = 22 × 101
96 = 2 × 2 × 2 × 2 × 2 × 3 = 25 × 3
H.C.F. = 22 = 4
L.C.M. = 25 × 3 × 101 = 9696
Now, H.C.F. × L.C.M. = 4 × 9696 = 38784
Product of numbers = 404 × 96 = 38784
Hence, H.C.F. × L.C.M. = Product of numbers.
Solution 2

Concept Insight: HCF is the product of common prime factors of all three numbers raised to least power, while LCM is product of prime factors of all here raised to highest power. Use the fact that HCF is always a factor of the LCM to verify the answer. Note HCF of (a,b,c) can also be calculated by taking two numbers at a time i.e HCF (a,b) and then HCF (b,c) .
Solution 3
Concept Insight: This problem must be solved using
product of two numbers = HCF x LCM rather than prime factorisation
Solution 3(ii)
The smallest number divisible by both 306 and 657 is the LCM if these numbers.
306 = 2 × 3 × 3 × 17 = 2 × 32 × 17
657 = 3 × 3 × 73 = 32 × 73
L.C.M. = 2 × 32 × 17 × 73 = 22338
Hence, the smallest number which is divisible by both 306 and 657 is 22338.
Solution 4
![]()
Solution 5
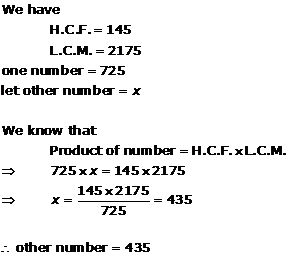
Solution 6

Solution 7
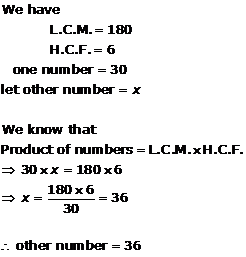
Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13

Solution 14
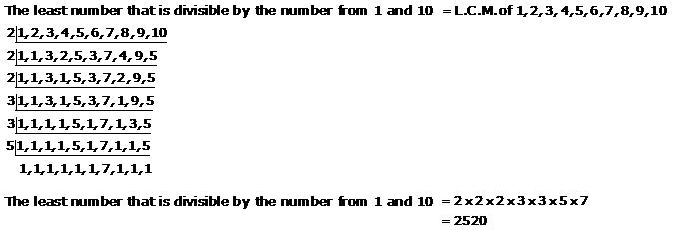
Solution 15

Solution 16

Solution 17
Required minimum distance each should walk so that they can cover the distance in complete step is the L.C.M. of 30 cm, 36 cm and 40 cm.
30 = 2 × 3 × 5;
36 = 22× 32;
40 = 23× 5
∴ LCM (30, 36, 40) = 23× 32× 5
∴ LCM = 23× 32× 5 = 360 cm.
Solution 18
Clearly, the required number is the H.C.F of the numbers
1251 - 1 = 1250, 9377 - 2 = 9375, and 15628 - 3 = 15625.
First we'll find the H.C.F of 1250 and 9375 by Euclid's algorithm as given below:
9375 = 1250 × 7 + 625
1250 = 625 × 2 + 0
Clearly, H.C.F of 1250 and 9375 is 625.
Let us now find the H.C.F of 625 and the third number 15625 by Euclid's algorithm:
15625 = 625 × 25 + 0
Hence, the required number is 625.
Real Numbers Exercise Ex. 1.5
Solution 1(i)

Solution 1(ii)

Solution 1(iii)

Solution 1(iv)

Solution 2(i)

Solution 2(ii)

Solution 2(iii)

Solution 2(iv)

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8
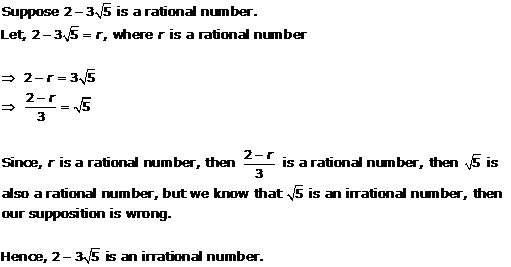
Solution 9

Solution 10

Solution 11
Let us assume that is a rational number.
So, there exist co-prime positive integers a and b such that
As is rational, so is rational.
Then, is also rational.
Thus, is rational.
But this is a contradiction to the fact that is an irrational number.
Hence, is an irrational number.
Solution 12
Let us assume that is a rational number.
So, there exist co-prime positive integers a and b such that
As is rational, so is rational.
Then, is also rational.
Thus, is rational.
But this is a contradiction to the fact that is an irrational number.
Hence, is an irrational number.
Solution 13
Let us assume that is a rational number.
So, there exist co-prime positive integers a and b such that
As is rational, so is rational.
Then, is also rational.
Thus, is rational.
But this is a contradiction to the fact that is an irrational number.
Hence, is an irrational number.
Solution 14

Real Numbers Exercise Ex. 1.6
Solution 1(i)

Solution 1(ii)
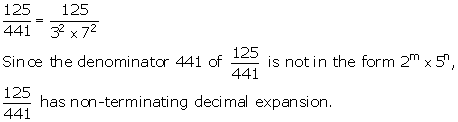
Solution 1(iii)

Solution 1(iv)
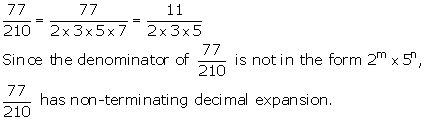
Solution 1(v)

Solution 1(vi)

Solution 2

Solution 3
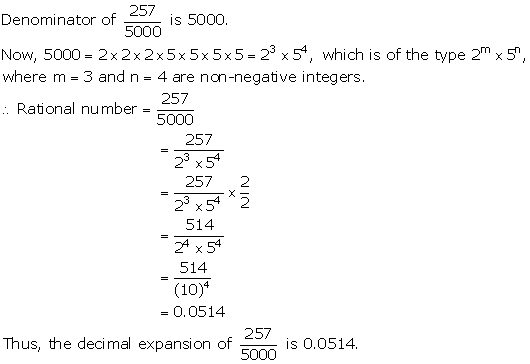
Solution 4

Solution 5

Real Numbers Exercise 1.59
Solution 1
Factorisation of 144 can be done as follows
so 144 = 2 × 2 × 2 × 2 × 3 × 3
= 24 × 32
Exponent of 2 in the prime factorisation of 144 is 4.
So, the correct option is (a).
Solution 2
We know that LCM of two numbers is divisible of HCF of these two numbers.
Hence
(a) 1200 is divisible by 600. So 600 can be the HCF.
(b) 500 cannot be the HCF because 1200 is not divisible by 500.
(c) 400 can be the HCF because 1200 is divisible by 400.
(d) 200 can be the HCF because 1200 is divisible by 200.
So, the correct option is (b).
Solution 3
n can also be written as
![]() 34 ×
23 × 53 × 5 × 7
34 ×
23 × 53 × 5 × 7
![]() 34 ×
(2 × 5)3 × 5 × 7
34 ×
(2 × 5)3 × 5 × 7
![]() 34 ×
5 × 7 × 103
34 ×
5 × 7 × 103
exponent of 10 in n is 3.
Hence number of consecutive zeros in n is 3.
So, the correct option is (b).
Solution 4
Factorisation of 196 is
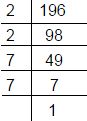
so 196 = 2 × 2 × 7 × 7
= 22 × 72
exponent of 2 is 2
exponent of 7 is 2
Hence sum of exponents is 4.
So, the correct option is (c).
Solution 5
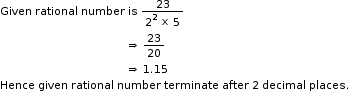
So, the correct option is (b).
Solution 6

So, the correct option is (a).
Solution 7
LCM (a, b) is
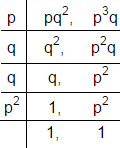
LCM (a, b) = p × q × q × p2
= p3q2
So, the correct option is (c).
Solution 8
HCF (a, b) is
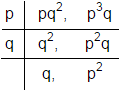
No further common division is possible
Hence HCF (a, b) = p × q
= pq
So, the correct option is (a).
Real Numbers Exercise 1.60
Solution 9
HCF of m, n is
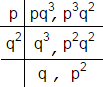
No further division is possible
Hence HCF is p × q2 = pq2
So, the correct option is (b).
Solution 10
We know,
LCM (a, b) × HCF (a, b) = a × b
So LCM (a, 18) × HCF (a, 18) = a × 18
![]() 36 ×
2 = a × 18
36 ×
2 = a × 18
![]() a
= 4
a
= 4
So, the correct option is (c).
Solution 11
HCF (95, 152)
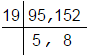
No further common division is possible.
Hence HCF (95, 152) is 19.
So, the correct option is (c).
Solution 12
We know
LCM (a, b) × HCF (a, b) = a × b
so LCM (26, 169) × HCF (26, 169) = 26 × 169
![]()
So, the correct option is (c).
Solution 13
LCM (a, b, c) is
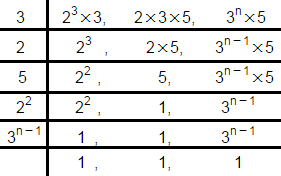
LCM (a, b, c) = 3 × 2 × 5 × 22 × 3n - 1
= 23 × 3n × 5 ........(1)
given that
LCM (a, b, c) = 23 × 32 × 5 ........(2)
from (1) & (2)
n = 2
So, the correct option is (b).
Solution 14
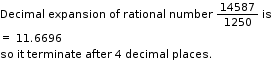
So, the correct option is (d).
Solution 15
If p and q are co-prime numbers then
HCF (p, q) = 1
After squaring the numbers, we get p2 and q2
If two numbers have HCF = 1 then after squaring the numbers their HCF remains equal to 1.
Hence HCF (p2 , q2) = 1
so p2 and q2 are co - prime numbers.
Ex : 2 and 3 are co - prime numbers.
HCF (2, 3) = 1
after squaring
HCF (4, 9) = 1
Hence, 4, 9 are also co - prime.
So, squares of two co - prime numbers are also co - prime.
So, the correct option is (a).
Solution 16

So, the correct option is (d).
*Note: Since the book has a typo error, the question has been modified.
Solution 17
It is given that 3 is the least prime factor of number a so a can be 3 (least possible value)
It is given that 7 is the least prime factor of number b so least possible value of b is 7.
Hence a + b = 10 (least possible value)
prime factors of 10 are 2 and 5
Hence the least prime factor of a + b is 2.
So, the correct option is (a).
Solution 18
We know that decimal expansion of a rational number is either terminating or non-terminating and recurring.
![]()
So the correct option is (b).
Solution 19

Solution 20

Solution 21
We know a2n - b2n is always divisible by a - b and a + b
On comparing with 92n - 42n, we get a = 9 & b = 4
Hence 92n - 42n is divisible by 9 - 4 & 9 + 4
= 5 & 13
So, the correct option is (c).
Real Numbers Exercise 1.61
Solution 22
6n always ends with 6
5n always ends with 5
Hence 6n - 5n always with 6 - 5 = 1
So, the correct option is (a).
Solution 23
(a) If two numbers are prime then their HCF must be 1 but LCM can't be 1
Example: 2, 3
LCM (2, 3) = 6
HCF (2, 3) = 1
(b) If two numbers are co - prime then their HCF must be 1 but LCM can't be 1.
(c) If two numbers are composite then their LCM and HCF can only be equal if the two numbers are same.
(d) If the numbers are equal.
Example: 6, 6
LCM (6, 6) = 6
HCF (6, 6) = 6
LCM = HCF
So, the correct option is (d).
Solution 24
Let numbers be a, b
It is given that LCM (a, b) + HCF (a, b) = 1260 ..........(1)
LCM (a, b) - HCF (a, b) = 900 ..........(2)
Adding equations (1) and (2), we get 2LCM (a, b) = 2160
Subtracting equations (1) and (2), we get 2HCF (a, b) = 360
So, LCM (a, b) = 1080 and
HCF (a, b) = 180
We know LCM (a, b) × HCF (a, b) = ab
ab = 1080 × 180
= 194400
So, the correct option is (b).
Solution 25

Solution 26
m is an integer.
⇒ m = ….., -2, -1, 0, 1, 2, …..
⇒ 2m = ……., -4, -2, 0, 2, 4, ……
Hence, correct option is (c).
Solution 27
q is an integer.
⇒ q = ….., -2, -1, 0, 1, 2, …..
⇒ 2q + 1 = ……., -3, -1, 0, 3, 5, ……
Hence, correct option is (d).
Solution 28
Let a = n2 - 1
Now, when n is odd, i.e. n = 2k + 1, we have
a = (2k + 1)2 - 1 =4k2 + 4k + 1 - 1 = 4k(k + 1)
At k = -1, we get
a = 4(-1)(-1 + 1) = 0, which is divisible by 8.
At k = 0, we get
a = 4(0)(0 + 1) = 0, which is divisible by 8.
At k = 1, we get
A = 4(1)(1 + 1) = 4(2) = 8, which is divisible by 8.
Hence, correct option is (c).
Solution 29
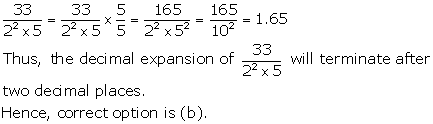
Solution 30
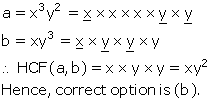
Solution 31

Solution 34
Euclid's division lemma states that for two positive integers a and b, there exist unique integers q and r such that a = bq + r, where r must satisfy 0 ≤ r < b.
Hence, correct option is (c).
Solution 32
The product of a non-zero rational number and an irrational number is always irrational.
Solution 33
Here, 12 = 22× 3, 21 = 3 × 7 and 15 = 3 × 5
HCF = 3
LCM = 22× 3 × 5 × 7 = 420