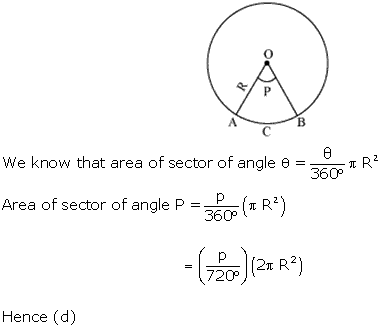ROUTERA

Chapter 12 Areas Related to Circles

Class 10th NCERT Maths Book Solution
CBSE Class 10 Maths
NCERT Solution

Areas Related to Circles Exercise Ex. 12.1

Solution 1

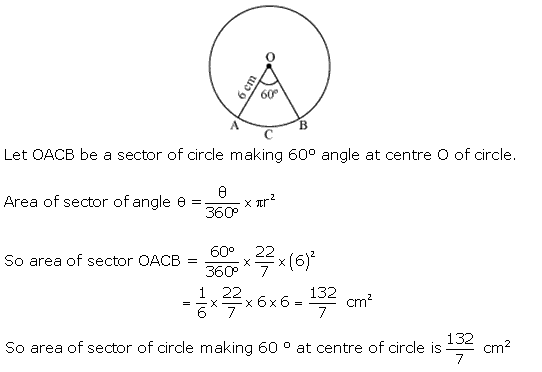
Solution 2

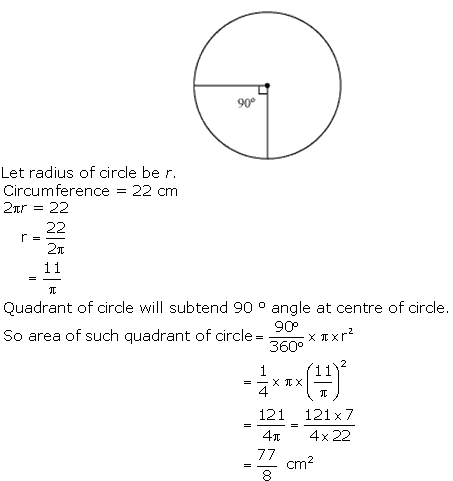
Solution 3

Solution 4

Solution 5

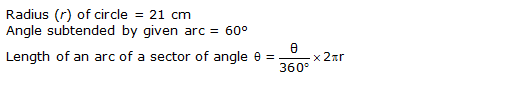
Solution 6


 

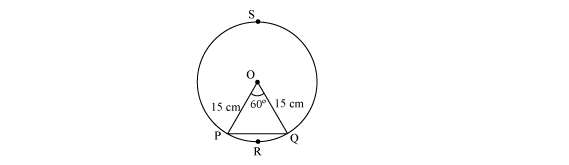
Radius (r) of the circle = 15

Area of sector OPRQ =fraction numerator 60 degree over denominator 360 degree end fraction cross times πr squared

=1 over 6 cross times 3.14 cross times 15 squared

=fraction numerator 706.5 over denominator 6 end fraction

= 117.75 cm2

In ∆OPQ

angle O P Q equals angle O Q P.... (Since OP = OQ)
 angle O P Q p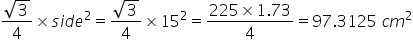lus angle O Q P plus angle P O Q equals 180 degree
\2 angle O P Q equals 120 degree

therefore angle O P Q equals 60 degree

∆OPQ is an equilateral triangle.

Area of ∆OPQ =fraction numerator square root of 3 over denominator 4 end fraction cross times s i d e squared equals fraction numerator square root of 3 over denominator 4 end fraction cross times 15 squared equals fraction numerator 225 cross times 1.73 over denominator 4 end fraction equals 97.3125 space c m squared

Area of segment PRQ = Area of sector OPRQ –Area of ∆OPQ

                                = 117.75 – 97.3125

                                = 20.4375 cm2

Area of major segment PSQ

= Area of circle – Area of segment PRQ

= 152p – 20.4375

= 3.14 × 225 – 20.4375

= 686.0625 cm2

Solution 7

 

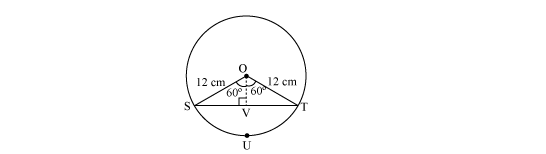
Draw a perpendicular OV on chord ST. It will bisect the chord ST.

SV = VT

In ∆OVS

fraction numerator O V over denominator O S end fraction equals cos space 60 degree

fraction numerator O V over denominator O S end fraction equals 1 half

OV = 6

fraction numerator S V over denominator S O end fraction equals sin space 60 degree equals fraction numerator square root of 3 over denominator 2 end fraction

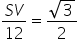
fraction numerator S V over denominator 12 end fraction equals fraction numerator square root of 3 over denominator 2 end fraction 

S V equals 6 square root of 3

ST = 2SV = 2 cross times 6 square root of 3 equals 12 square root of 3

Area of ∆OST = 1 half cross times S T cross times O V

= 1 half cross times 12 square root of 3 cross times 6

= 36 square root of 3

= 36 × 1.73

= 62.28

Area of sector OSUT = fraction numerator 120 degree over denominator 360 degree end fraction cross times straight pi cross times 12 squared

= 150.72

Area of segment SUT = Area of sector OSUT

                                = 150.72 – 62.28

                                = 88.44 cm2

Solution 8

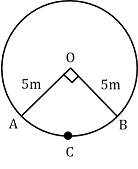
The horse can graze a sector of 90° in a circle of 5 m radius.

i.     So area that can be grazed by horse = area of sector OACB

        = fraction numerator 90 degree over denominator 360 degree end fraction cross times πr squared

       = 1 fourth cross times 3.14 cross times 5 squared

       = 19.63 m2

ii.    Area that can be grazed by the horse when the length of rope is 10 m long = fraction numerator 90 degree over denominator 360 degree end fraction cross times pi cross times 10 squared

       = 1 fourth cross times 3.14 cross times 100

       = 78.5

Change in grazing area = 78.5 – 19.63 = 58.87 cm2

Solution 9

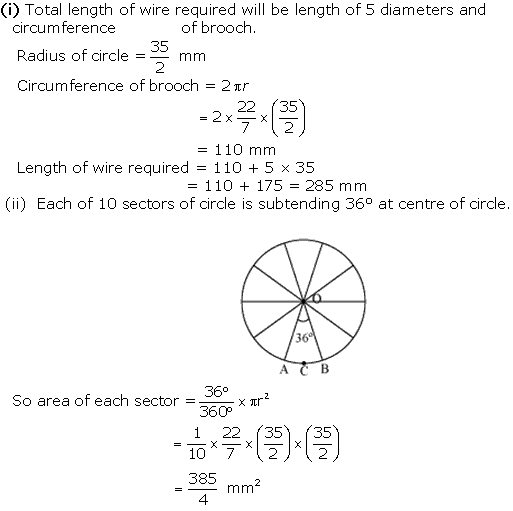
Solution 10

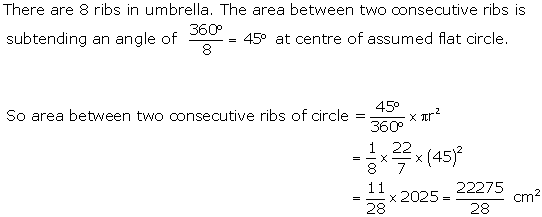
Solution 11

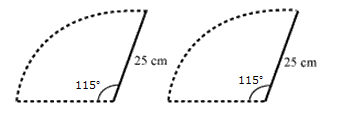
The figure shows that each blade of the wiper will sweep an area of a sector of 115° in a circle of 25 cm radius.

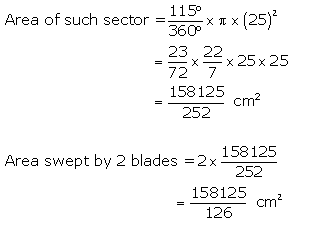
Solution 12

Solution 13



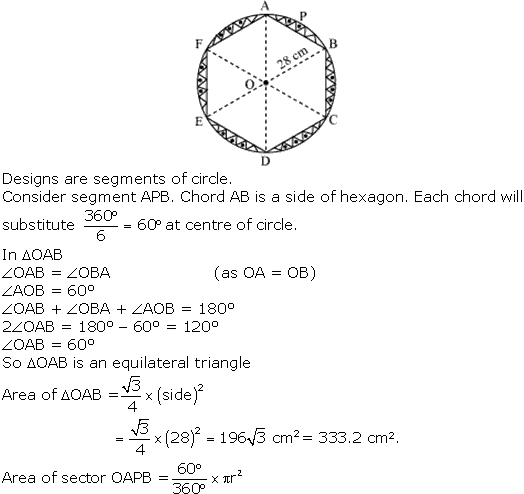
Solution 14