Chapter 9 Circles

NCERT Exemplar Class 10 Maths Chapter 9 Circles

Exercise 9.1

Choose the correct answer from the given four options:

Question 1
If radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is
(A) 3 cm
(B) 6 cm
(C) 9 cm
(D) 1 cm
Solution:
(B) Let O be the centre of two concentric circles C₁ and C₂, whose radii are r₁ = 4 cm and r₂ = 5 cm.
Now, we draw a chord AC of circle C₂, which touches the circle Q at B.
Also, join OB, which is perpendicular to AC.
[∵ Tangent at any point of circle is perpendicular to radius through the point of contact]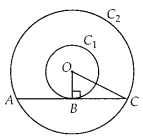

Now, in right angled ∆OBC,
OC² = BC² + BO² [By Pythagoras theorem]
⇒ 5² = BC² + 4²
⇒ BC² = 25 – 16 = 9
⇒ BC = 3 cm
∴ Length of chord AC = 2BC = 2 x 3 = 6 cm

Question 2
In figure, if ∠AOB = 125°, then ∠COD is equal to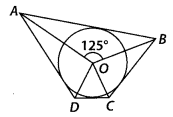

(A) 62.5°
(B) 45°
(C) 35°
(D) 55°
Solution:
(D) We know that the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
⇒ ∠AOB + ∠COD = 180°
⇒ ∠COD = 180° – ∠AOB
= 180° – 125° = 55°

Question 3
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at the point A, then ∠BAT is equal to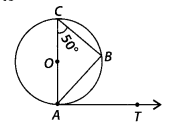

(A) 65°
(C) 50°
(B) 60°
(D) 40°
Solution:
(C) In figure, AOC is a diameter of the circle. We know that, diameter subtends an angle 90° at the circle.
So, ∠ABC = 90°
In ∆ACB,
∠A + ∠B + ∠C = 180° [Angle sum property]
⇒ ∠A + 90° + 50° = 180°
⇒ ∠A + 140° = 180°
⇒ ∠A = 180° – 140° = 40°
⇒ ∠A or ∠OAB = 40°
Since, AT is the tangent to the circle at point A. Therefore, OA is perpendicular to AT.
∠OAT = 90°
⇒ ∠OAB + ∠BAT =90°
On putting ∠OAB = 40°, we get
⇒ ∠BAT =90° -40° = 50°
Hence, the value of ∠BAT is 50°.

Question 4
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is
(A) 60 cm²
(B) 65 cm²
(C) 30 cm²
(D) 32.5 cm²
Solution:
(A) Firstly, draw a circle of radius 5 cm with centre O. P is a point at a distance of 13 cm from O. A pair of tangents PQ and PR are drawn.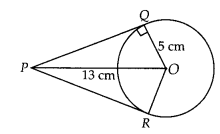

Thus, quadrilateral PQOR is formed.
∵ OQ ⊥ QP [since, QP is a tangent line]
In right angled ∆PQO,
OP² = OQ² + QP²
⇒ 13² = 5² + QP²
⇒ QP² = 169 – 25 = 144
⇒ QP = 12 cm
Now, area of ∆OQP = \(\frac { 1 }{ 2 }\) x QP x QO
= \(\frac { 1 }{ 2 }\) x 12 x 5 = 30 cm²
∴ Area of quadrilateral PQOR = 2 x ar ∆OQP
= 2 x 30 = 60 cm²

Question 5
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XT and at a distance 8 cm from A is
(A) 4 cm
(B) 5 cm
(C) 6 cm
(D) 8 cm
Solution:
(D) First, draw a circle of radius 5 cm with centre O. A tangent XY is drawn at point A.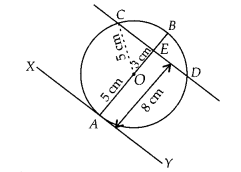

A chord CD is drawn which is parallel to XY and at a distance of 8 cm from A.
Now, ∠OAY = 90°
[ ∵ Tangent at any point of circle is perpendicular to the radius through the point of contact]
∠OAY +∠OED= 180°
[ ∵ Sum of cointerior angles is 180°]
⇒ ∠OED = 180° – 90° = 90°
Also, AE = 8 cm Join OC.
OC = 5 cm [Radius of circle]
OE = AE-OA = 8 – 5 = 3 cm
Now, in right angled ∆OEC,
OC² = OE² + EC² [By Pythagoras theorem]
⇒ EC² = OC² – OE²
⇒ EC² = 5² – 3²
⇒ EC² = 25 – 9 = 16
⇒ EC = 4 cm
Since, perpendicular from centre to the chord bisects the chord.
∴ CE = ED
⇒ CD = 2 x EC
⇒ CD = 2 x 4
⇒ CD = 8 cm

Question 6
In figure, ATis a tangent to the circle with centre O such that 07 = 4 cm and ∠OTA = 30°. Then AT is equal to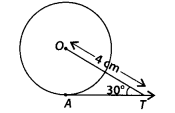

(A) 4cm
(B) 2cm
(C) 2√3cm
(D) 4√3cm
Solution:
(C) Join OA.
We know that, the tangent at any point of a circle is perpendicular to the radius through the point of contact.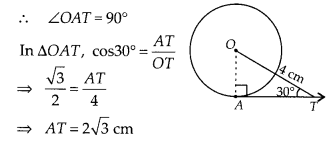

Question 7
In figure, if O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 500 with PQ, then ∠POQ is equal to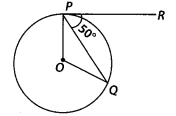

(A) 100°
(B) 80°
(C) 90°
(D) 75°
Solution:
(A) Given, ∠QPR = 50°
We know that, the tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ ∠OPR = 90°
⇒ ∠OPQ + ∠QPR = 90°
⇒ ∠OPQ = 90° – 50° = 40° [ ∵ ∠QPR = 50°]
Now, OP = OQ = radius of circle
∴ ∠OQP = ∠OPQ = 40°
[Angles opposite to equal sides are equal]
In ∆OPQ,
∠O + ∠OPQ + ∠Q = 180° [Angle sum property]
⇒ ∠POQ = 180° – (40 + 40°)
= 180° – 80°
[∵ ∠OPQ = 40° = ∠Q]
⇒ ∠POQ = 100°

Question 8
In figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to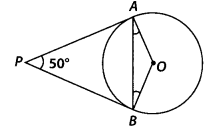

(A) 25°
(B) 30°
(C) 40°
(D) 50°
Solution:
(A) Given, PA and PB are tangent lines.
∴ PA = PB [∵ Length of tangents drawn from an external point to a circle is equal]
∠PBA = ∠PAB = θ (say)
In ∆PAB,
∠P + ∠A + ∠B = 180° [Angle sum property]
⇒ 50° + θ + θ= 180°
⇒ 20 = 180° – 50° = 130°
⇒ θ = 65°
Also, OA ⊥ PA
[∵ Tangent at any point of a circle is perpendicular to the radius through the point of contact]
∴ ∠PAO = 90°
⇒ ∠PAB + ∠BAO = 90°
⇒ 65° + ∠BAO = 90°
⇒ ∠BAO = 90° – 65° = 25°
⇒ ∠OAB = 25°

Question 9
If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then length of each tangent is equal to

Solution:
(D) Let P be an external point and a pair of tangents is drawn from point P such that the angle between two tangents is 60°.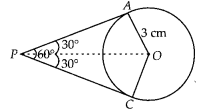

Join OA and OP.
Also, OP is a bisector line of ∠APC.
∴ ∠APO = ∠CPO = 30°
Also, OA ⊥ AP
[Tangent at any point of a circle is perpendicular to the radius through the point of contact.]
∴∠OAP = 90°
In right angled ∆OAP,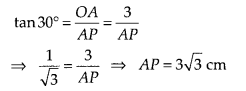

Hence, the length of each tangent is 3√3 cm.

Question 10
In figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to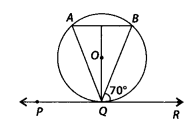

(A) 20°
(B) 40°
(C) 35°
(D) 45°
Solution:
(B) Given, AB ॥ PR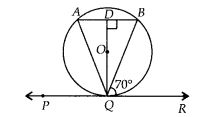

∴ ∠ABQ = ∠BQR = 70° [Alternate angles]
Also, QD is perpendicular to AB and QD bisects AB.
In ∆QDA and ∆QDB,
∠QDA = ∠QDB [90° each]
AD = BD
QD = QD [Common side]
∆ADQ ≅ ∆BDQ [by SAS congruency]
⇒ ∠QAD = ∠QBD [CPCT] …(i)
But ∠QBD = ∠ABQ = 70°
⇒ ∠QAD = 70° [From (i)]
Now, in ∆ABQ, ∠A + ∠B + ∠AQB = 180°. [Angle sum property]
⇒ ∠AQB = 180° – (70° + 70°) = 40°

Exercise 9.2

Write ‘True’ or ‘False’ and justify your answer in each of the following:

Question 1
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
Solution:
False
Since a chord AB subtends an angle of 60° at the centre of a circle.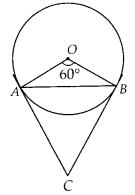

⇒ ∠AOB = 60°
As OA = OB = Radius of the circle
∠OAB = ∠OBA = 60°
[∵ Angles opposite to equal sides are equal]
The tangent at points A and B is drawn, which intersect at C.
We know, OA ⊥ AC and OB ⊥ BC.
∴ ∠OAC = 90° and ∠OBC = 90°
⇒ ∠OAB + ∠B AC = 90° and ∠OBA + ∠ABC = 90°
⇒ ∠BAC = 90° – 60° = 30° and ∠ABC = 90° – 60° = 30°
In ∆ABC,
∠BAC + ∠CBA + ∠ACB = 180°
[Angle sum property]
⇒ ∠ACB = 180° – (30° + 30°) = 120°

Question 2
The length of tangent from an external point on a circle is always greater than the radius of the circle.
Solution:
False
Because the length of tangent from an external point P on a circle may or may not be greater than the radius of the circle.

Question 3
The length of tangent from an external point P on a circle with centre O is always less than OP.
Solution:
True
PT is a tangent drawn from an external point P. Join OT
∵ OT ⊥ PT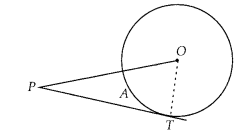

So, OTP is a right angled triangle formed.
In right angled triangle, hypotenuse is always greater than any of the two sides of the triangle.
∴ OP > PT or PT< OP

Question 4
The angle between two tangents to a circle may be 0°.
Solution:
True
This may be possible only when both tangent lines coincide or are parallel to each other.

Question 5
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = a√2.
Solution:
True
From point P, two tangents are drawn.
Given, OT = a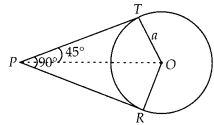

Also, line OP bisects the ∠RPT
∴ ∠TPO = ∠RPO = 45°
Also, OT ⊥ TP ⇒ ∠OTP = 90°
In right angled ∆OTP,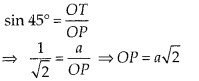

Question 6
If angle between two tangents drawn from a point P to a circle of radius a and centre 0 is 60°, then OP = a√3.
Solution:
False
From point P, two tangents are drawn.
Given, OT= a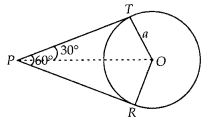

Also, line OP bisects the ∠RPT.
∴∠TPO = ∠RPO = 30°
Also, OT ⊥ PT
⇒ ∠OTP = 90°
In right angled ∆OTP,
sin 30° = \(\frac { OT }{ OP }\) ⇒ \(\frac { 1 }{ 2 }\) = \(\frac { a }{ OP }\)
⇒ OP = 2a

Question 7
The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
Solution:
True
Let EAF be tangent to the circumcircle of ∆ABC.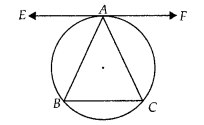

To prove: EAF ॥ BC
We have, ∠EAB = ∠ACB …(i)
[Angle between tangent and chord is equal to angle made by chord in the alternate segment]
Here, AB = AC
⇒ ∠ABC = ∠ACB …(ii)
From equation (i) and (ii), we get
∠EAB = ∠ABC
∵ Alternate angles are equal.
⇒ EAF ॥ BC

Question 8
If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.
Solution:
False
Given that PQ is any line segment and S₁, S₂, S₃, S₄, …….. circles touch the line segment PQ at a point A. Let the centres of the circles S₁, S₂, S₃, S₄, ……….. be C₁, C₂, C₃, C₄, ……… respectively.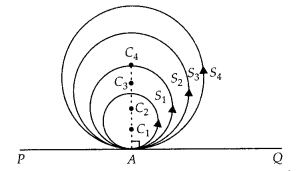

To prove: Centres of the circles lie on the perpendicular bisector of PQ.
Joining each centre of the circles to the point A on the line segment PQ by line segment i.e., C₁A, C₂A, C₃A, C₄A,… and so on.
We know that, if we draw a line from the centre of a circle to its tangent line, then the line is always perpendicular to the tangent line. But it does not bisect the line segment PQ.

Question 9
If a number of circles pass through the end points P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
Solution:
True
We draw two circles with centre C₁ and C₂ passing through the end points P and Q of a line segment PQ. We know that the perpendi-cular bisector of a chord of circle always passes through the centre of the circle.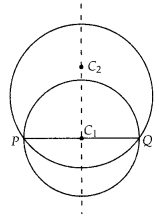

Thus, perpendicular bisector of PQ passes through C₁ and C₂ . Similarly, all the circle passing through the end points of line segment PQ, will have their centres on the perpendicular bisector of PQ.

Question 10
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
Solution:
True
To prove: BC = BD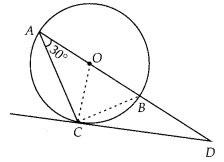

Join BC and OC.
Given, ∠BAC = 30°
⇒ ∠BCD = 30°
[Angle between tangent and chord is equal to angle made by chord in the alternate segment]
∵ OC ⊥ CD and OA = OC = radius
⇒ ∠OAC = ∠OCA = 30°
∠ACD = ∠ACO + ∠OCD = 30° + 90° = 120°
In ∆ACD,
∠DAC + ∠ACD + ∠CDA = 180° [Angle sum property]
⇒ 30° + 120° + ∠CDA = 180°
⇒ ∠CDA = 180° – (30° + 120°) = 30°
∠CDA = ∠BCD
⇒ BC = BD
[∵ Sides opposite to equal angles are equal]

Exercise 9.3

Question 1
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
Solution:
Let C₁ and C₂ be the two circles having same centre O. AC is a chord which touches C₁ at point D.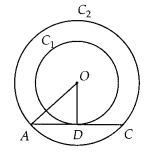

Join OD.
Also, OD ⊥ AC
∴ AD = DC = 4 cm
[Perpendicular line OD bisects the chord]
In right angled ∆AOD,
OA² = AD² + OD² [By Pythagoras theorem]
⇒ OD² = 52 – 42
⇒ OD² = 25 – 16 = 9
⇒ OD = 3 cm
∴ Radius of the inner circle is OD = 3 cm

Question 2
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
Solution: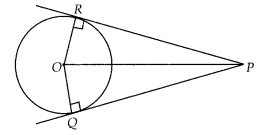

To prove: QORP is a cyclic quadrilateral.
Since, PR and PQ are tangents.
∴ OR ∠ PR and OQ ∠ PQ
⇒ ∠ORP = ∠OQP = 90°
Hence, ∠ORP + ∠OQP = 180°
Also, in quadrilateral QORP,
∠ORP + ∠OQP + ∠ROQ + ∠QPR = 360°
⇒ 180° + ∠ROQ + ∠QPR = 360°
⇒ ∠ROQ + ∠QPR = 180°
∵ If sum of opposite angles in quadrilateral is 180°, then the quadrilateral is cyclic.
⇒ QORP is cyclic quadrilateral.

Question 3
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
Solution: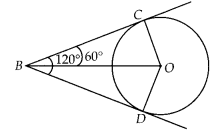

To prove: BO = 2BC
Given, ∠DBC = 120°
Join OC, OD and BO.
Since, BC and BD are tangents.
∴ OC ⊥ BC and OD ⊥ BD
We know, OB is the angle bisector of ∠DBC.
∴∠OBC = ∠DBO = 60°
In right angled ∆OBC,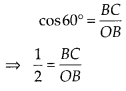

⇒ OB = 2 BC
Also, BC = BD
[Tangent drawn from external point to circle are equal]
OB = BC + BC
⇒ OB = BC + BD

Question 4
Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of angle formed by tangents..
Solution:
Given, two tangents PQ and PR are drawn from an external points P to a circle with centre O.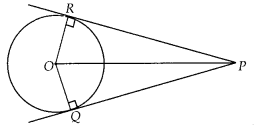

To prove: Centre of a circle touching two intersecting lines lies on the angle bisector of angle formed by tangents.
Construction: Join OR and OQ.
In ∆POR and ∆POQ,
∠PRO = ∠PQO = 90°
[tangent at any point of a circle is perpendicular to the radius through the point of contact]
OR = OQ [Radii of same circle]
OP = OP [Common side]
∆ PRO ≅ ∆ PQO [RHS criterion]
Hence, ∠RPO = ∠QPO [By CPCT]
Thus, O lies on angle bisector of ∠RPQ.

Question 5
In figure, AB and CD are common tangents to two circles of unequal radii.
Prove that AB = CD.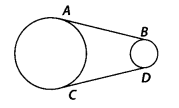

Solution:
Given, AB and CD are common tangents to two circles of unequal radii.
To prove : AB = CD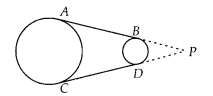

Construction: Extend AB and CD, to intersect at P.
PA = PC
[∵ Length of tangents drawn from an external point to a circle is equal]
Also, PB = PD
∴PA – PB = PC – PD
⇒ AB = CD

Question 6
In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
Solution: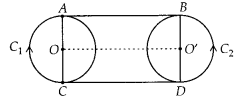

Join OO’
Since, OA = O’B [Given]
Also, ∠OAB = ∠O’BA = 90°
[Tangent at any point of a circle is perpendicular to the radius at the point of contact]
Since, perpendicular distance between two straight lines at two different points is same.
⇒ AB is parallel to OO’
Similarly, CD is parallel to OO’
⇒AB ॥ CD
Also, ∠OAB = ∠OCD = ∠O’BA = ∠O’DC = 90°
⇒ ABCD is a rectangle.
Hence, AB = CD.

Question 7
In figure, common tangents AB and CD to two circles intersect at E.
Prove that AB = CD.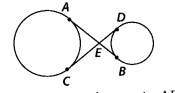

Solution:
Given, common tangents AB and CD to two circles intersecting at E.
To prove: AB = CD
∵ The length of tangents drawn from an external point to a circle is equal
∴ EB = ED and EA = EC
On adding, we get
EA + EB = EC + ED
⇒ AB = CD

Question 8
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
Solution:
Given, chord PQ is parallel to tangent at R.
To prove : R bisects the arc PRQ.

∠1 = ∠2 [Alternate interior angles]
∠1 = ∠3 [Angle between tangent and chord is equal to angle made by chord in alternate segment]
⇒ ∠2 = ∠3
⇒ PR = QR [Sides opposite to equal angles are equal]
⇒ arc PR = arc QR
So, R bisects PQ.

Question 9
Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
Solution:
To prove : ∠1 = ∠2
Let RQ be a chord of the circle. Tangents are drawn at the points R and Q.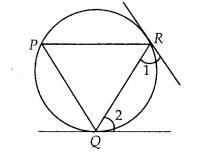

Let P be another point on the circle, then join PQ and PR.
Since, at point Q, there is a tangent.
∠2 = ∠P [Angles in alternate
segments are equal] Since, at point R, there is a tangent.
∴ ∠1 = ∠P [Angles in alternate segments are equal]
∴ ∠1 = ∠2 = ∠P
⇒ ∠1 = ∠2

Question 10
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
Solution:
Given, AB is a diameter of the circle.
A tangent is drawn at point A.
Draw a chord CD parallel to tangent MAN.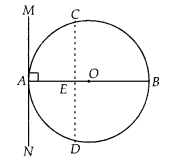

So, CD is a chord of the circle and OA is radius of the circle.
∴ ∠MAO = 90°
[tangent at any point of a circle is perpendicular to the radius through the point of contact]
⇒ ∠CEO = ∠MAO [Corresponding angles]
∴ ∠CEO = 90°
Thus, OE bisects CD,
[Perpendicular from centre of circle to chord bisects the chord]
Similarly, diameter AB bisects all chords which are parallel to the tangent at the point A.

Exercise 9.4

Question 1
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
Solution:
Given, a hexagon ABCDEF circumscribes a circle.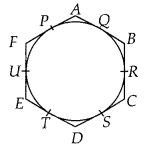

To prove : AB + CD + EF = BC + DE + FA
∵ AQ = AP
QB = BR
CS = CR
DS = DT
EU = ET
UF = FP
[Tangents drawn from an external point to a circle are equal]
AB + CD + EF = (AQ + QB) + (CS + SD) + (EU + UF) = (AP + BR) + (CR + DT) + (ET + FP)
= (AP + FP) + (BR + CR) + (DT + ET)
= AF + BC + DE
⇒ AB + CD + EF = AF + BC + DE

Question 2
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F respectively, prove that BD = s – b.
Solution: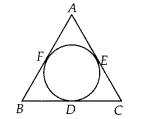

Given, BC = a, CA = b and AB = c
Since, tangents drawn from an external point to the circle are equal in length.
∴ BD = BF = x (say)
DC = CE = y (say)
and AE = AF = 2 (say)
Now, BC + CA + AB = a + b + c
⇒ (BD + DC) + (CE + EA) + (AF + FB) = a + b + c
⇒ (x + y) + (y + z) + (z + x) = a + b + c
⇒ 2(x + y + z) = 2s
[ ∵ 2s = a + b + c = perimeter of ∆ABC]
⇒ s = x + y + z
⇒ x = s – (y + z)
⇒ BD = s – b [∵ b = AE + EC = z + y]

Question 3
From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the perimeter of the triangle PCD.
Solution:
∵ Tangents from an external point to a circle are equal in length.
∴ CE = CA, DE = DB and PA = PB.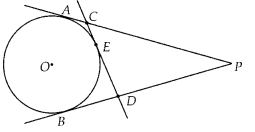

Perimeter of ∆PCD = PC + CD + PD
= PC + CE + ED + PD
= PC + CA + DB + PD
= PA + PB
= 2PA = 2 x 10 = 20 cm

Question 4
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB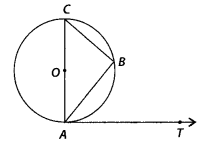

Solution:
Since, AC is a diameter line, so angle in semi-circle formed is 90°.
i.e., ∠ABC = 90°
In ∆ABC,
∠CAB + ∠ABC + ∠BCA = 180° [Angle sum property]
⇒ ∠CAB + ∠BCA = 180°-90° = 90° ,..(i)
Since, diameter of a circle is perpendicular to the tangent.
i.e., CA ⊥ AT
∴ ∠CAT = 90°
⇒ ∠CAB + ∠BAT =90° …(ii)
From equation (i) and (ii),
∠CAB + ∠ACB = ∠CAB + BAT
⇒ ∠ACB = ∠BAT

Question 5
Two circles with centres O and O’ of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O’P are tangents to the two circles. Find the length of the common chord PQ.
Solution:
Here, two circles are of radii OP = 3 cm and O’P = 4 cm.
These two circles intersect at P and Q.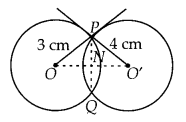

Here, OP and O’P are two tangents drawn at point P.
∠OPO’ = 90° [Tangent at any point of circle is perpendicular to radius through the point of contact]
Join OO’ and PQ such that OO’ and PQ intersect at point N.
In right angled ∆OPO’,
(OO’)² = (OP)² + (PO’)² [By Pythagoras theorem]
⇒ (OO’)² = (3)² + (4)² = 25
⇒ OO’ = 5 cm
Also, PN ⊥ OO’
Let ON = x, then NO’ = 5 – x
In right angled ∆ONP,
(OP)² = (ON)² + (NP)² [By Pythagoras theorem]
⇒ (NP)² = 3² – x² = 9 – x² …(i)
and in right angled ∆PNO’,
(PO’)² = (PN)² + (NO’)² [By Pythagoras theorem]
⇒ (4)² = (PN)² + (5 – x)²
⇒ (PN)² = 16- (5 -x)² …(h)
From equation (i) and (ii),
9 -x² = 16 – (5 -x)²
⇒ 7 + x² – (5 – x)² = 0
⇒ 7 + x² -(25 + x² – 10x) = 0
⇒ 10x = 18
∴ x = 1.8
Again, in right angled ∆OPN,
OP² = (ON)² + (NP)² [By Pythagoras theorem]
⇒ 3²= (1.8)² + (NP)²
⇒ (NP)² = 9 – 3.24 = 5.76
⇒ NP = 2.4
∴ Length of common chord,
PQ = 2PN = 2 x 2.4 = 4.8 cm

Question 6
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC at P. Prove that the tangent to the circle at P bisects BC.
Solution:
Let O be the centre of the given circle. Suppose, the tangent at P meets BC at Q. Join BP.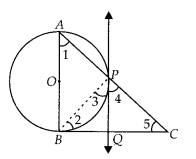

To prove: BQ = QC
∠ABC = 90° [Given]
In ∆ABC, ∠1 + ∠5 = 90° [Angle sum property, ∠ABC = 90°]
∠3 = ∠1 [Angle between tangent and the chord equals angle made by the chord in alternate segment]
⇒ ∠3 + ∠5 = 90° …(i)
Also, ∠APB = 90° [Angle in semi-circle]
∠APB + ∠BPC = 180°
∴ 90° + ∠3 + ∠4 = 180°
⇒ ∠3 + ∠4 = 90° …(ii)
From equations (i) and (ii), we get ∠3 + ∠5 = ∠3 + ∠4
⇒ ∠5 = ∠4
⇒ PQ = QC [Sides opposite to equal angles are equal]
Also, QP = QB
[tangents drawn from an external point to a circle are equal]
⇒ QB = QC
⇒ PQ bisects BC.

Question 7
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.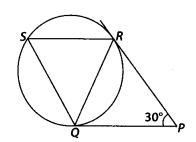

Solution:
PQ and PR are two tangents drawn from an external point P.
∴ PQ = PR
[Lengths of tangents drawn from an external point to a circle are equal]
⇒ ∠PQR = ∠QRP
[Angles opposite to equal sides are equal]
Now, in ∆PQR,
∠PQR + ∠QRP + ∠RPQ = 180° [Angle sum property]
⇒ ∠PQR + ∠PQR + 30° = 180°
⇒ 2∠PQR = 180° – 30° = 150°
[∵ ∠PQR = ∠QRP]
⇒ ∠PQR = 75°
Since, SR ॥ QP
∠SRQ = ∠RQP = 75° [Alternate interior angles]
Also, ∠PQR = ∠QSR = 75° [Angles in alternate segment]
In ∆QRS,
∠Q + ∠R + ∠S = 180° [Angle sum property]
⇒ ∠Q = 180° – (75° + 75°) = 30°
∴ ∠RQS = 30°

Question 8
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°.The tangent at C intersects extended AB at a point D. Prove that BC = BD.
Solution:
Given, AB is a diameter and AC is a chord of circle with centre O, ∠BAC = 30°
To prove : BC = BD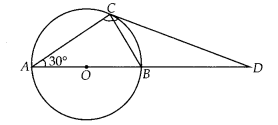

Join BC
∠BCD = ∠CAB [Angles in alternate segment]
∠CAB = 30° [Given]
∠BCD = 30° …(i)
∠ACB = 90° [Angle in semi-circle]
In ∆ABC,
∠A + ∠B + ∠C = 180° [Angle sum property]
30° + ∠CBA + 90° = 180°
⇒ ∠CBA = 60°
Also, ∠CBA + ∠CBD = 180° [Linear pair]
⇒ ∠CBD = 180° – 60° = 120°
[∵ ∠ CBA = 60°]
Now, in ACBD,
∠CBD + ∠BDC + ∠DCB = 180°
⇒ 120° + ∠BDC + 30° = 180°
⇒ ∠BDC = 30° …(ii)
From (i) and (ii),
∠BCD = ∠BDC
⇒ BC = BD
[Sides opposite to equal angles are equal]

Question 9
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
Solution:
Let mid-point of an arc AMB be M and TMT’ be the tangent to the circle.
Join AB, AM and MB.
Since arc AM = arc MB =3 Chord AM = Chord MB
In ∆AMB, AM = MB
⇒ ∠MAB = ∠MBA …(i)
[Sides opposite to equal angles are equal]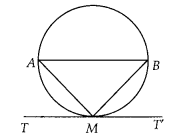

Since, TMT’ is a tangent line.
∴ ∠AMT = ∠MBA [Angles in alternate segments are equal]
= ∠MAB [from equation (i)]
But ∠AMT and ∠MAB are alternate angles, which is possible only when AB ॥ TMT
Hence, the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.

Question 10
In figure, the common tangent, AB and CD to two circles with centres O and O’ intersect at E. Prove that the points O, E, O’ are collinear.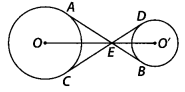

Solution:
Join AO, OC and O’D, O’B.
Now, in ∆EO’D and ∆EO’B,
O’D = O’B
O’E = O’E
ED = EB
[Tangents drawn from an external point to the circle are equal in length]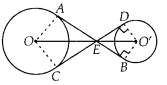

∴ EO’D ≅ ∆ EO’B [By SSS congruence criterion]
⇒ ∠O’ED = ∠O’EB …(i)
i.e., O’E is the angle bisector of ∠DEB.
Similarly, OE is the angle bisector of ∠AEC. Now, in quadrilateral DEBO’.
∠O’DE = ∠O’BE = 90°
[CED is a tangent to the circle and O’D is the radius, i.e., O’D ⊥ CED]
⇒ ∠O’DE + ∠O’BE = 180°
∴ ∠DEB + ∠DO’B = 180°
[∵ DEBO’ is cyclic quadrilateral] …(ii)
Since, AB is a straight line.
∴ ∠AED + ∠DEB = 180°
⇒ ∠AED + 180° – ∠DO’B = 180° [from (ii)]
⇒ ∠AED = ∠DO’B …(iii)
Similarly, ∠AED = ∠AOC …(iv)
Again from eq. (ii), ∠DEB = 180° – ∠DO’B
Dividing by 2 on both sides, we get


So, OEO’ is straight line.
Hence, O, E and O’ are collinear.

Question 11
In figure, O is the centre of a circle of radius 5 cm, T is a point such that 07= 13 cm and 07 intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.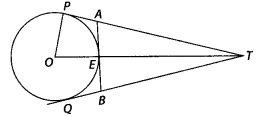

Solution:
OP is perpendicular to PT.
∴ In ∆OPT,
OT² = OP² + PT²
⇒ PT² = OT² – OP²
⇒ PT² = (13)² – (5)² = 169 – 25 = 144
⇒ PT= 12 cm
Since, the length of pair of tangents from an external point T is equal.
∴ QT= 12 cm
Now, TA = PT – PA
⇒ TA = 12 -PA …(i)
and TB = QT – QB
TB = 12 – QB …(ii)
Also, PA = AE and QB = EB …(iii) [Pair of tangents]
∴ ET = OT – OE [∵ OE = 5 cm = radius]
⇒ ET = 13 – 5
⇒ ET = 8 cm
Since, AB is a tangent and OE is the radius.
∴OE ⊥ AB
⇒ ∠OEA = 90°
∴ ∠AET = 180° – ∠OEA [Linear pair]
⇒ ∠AET = 90°
Now, in right angled ∆AET,
(AT)² = (AE)² + (ET)² [by Pythagoras theorem]
⇒ (12 – PA)² = (PA)² + (8)²
⇒ 144 + (PA)² – 24 PA = (PA)² + 64
⇒ 24 PA = 80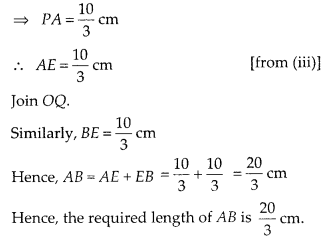

Question 12
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, Find ∠CBA.
Solution: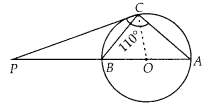

Join OC. Here, OcC is the redius.
Since, tangent at any point of a circle is – perpendicular to the radius through the point of contact.
∴ OC ⊥ PC
Now, ∠PCA = 110° [Given]
⇒ ∠PCO + ∠OCA = 110°
⇒ 90° + ∠OCA = 110°
⇒ ∠OCA = 20°
∵ OC = OA = radius of circle
∴ ∠OCA = ∠OAC = 20°
[Sides opposite to equal angles are equal]
Since, PC is a tangent,
∠BCP = ∠CAB = 20° [Angles in alternate segment]
In ∆PAC,
∠P + ∠C + ∠A = 180°
∠P = 180° – (∠C + ∠A)
= 180°-(110°+ 20°)
= 180° – 130° = 50°
In ∆PBC,
∠BPC + ∠PCB + ∠CBP = 180°
⇒ 50° + 20° + ∠PBC = 180°
⇒ ∠PBC = 180° – 70°
⇒ ∠PBC = 110°
Since, ABP is a straight line.
∴ ∠PBC + ∠CBA = 180°
⇒ ∠CBA = 180° – 110° = 70°

Question 13
if an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.
Solution:
Join OB, OC and OA.
In ∆ABO and ∆ACO,
AB = AC [Given]
BO = CO [Radii of same circle]
AO = AO [Common side]
∴ ∆ABO ≅ ∆ACO [By SSS congruence criterion]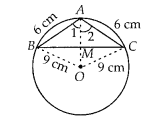

⇒ ∠1 = ∠2 [CPCT]
Now, in ∆ABM and ∆ACM,
AB = AC [Given]
∠1 = ∠2 [proved above]
AM = AM [Common side]
∴ ∆AMB ≅ ∆AMC [By SAS congruence criterion]
⇒ ∠AMB = ∠AMC [CPCT]
Also, ∠AMB + ∠AMC = 180° [Linear pair]
⇒ ∠AMB = 90°
We know that a perpendicular from the centre of circle bisects the chord.
So, OA is a perpendicular bisector of BC.
Let AM = x, then OM = 9 – x [ ∵ OA = radius = 9 cm]
In right angledd ∆AMC,
AC² = AM² + MC²
[By Pythagoras theorem]
⇒ MC² = 6² – x² …(i)
In right angle ∆OMC,
OC² = OM² + MC² [By Pythagoras theorem]
⇒ MC² = 9² – (9 – x)²
From equation (i) and (ii),
6² – x² = 9² – (9 – x)²
⇒ 36 – x² = 81 – (81 + x² – 18x)
⇒ 36 = 18x
⇒ x = 2
∴ AM = 2 cm
From equation (ii),
MC² = 9² – (9 – 2)²
⇒ MC² = 81 – 49 = 32
⇒ MC = 4√2 cm
∴ BC = 2 MC = 8√2 cm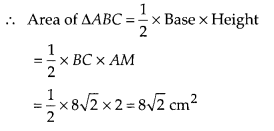

Fience, the required area of ∆ABC is 8√2 cm².

Question 14
1 is a point at a distance 13 cm from the centre 0 of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
Solution: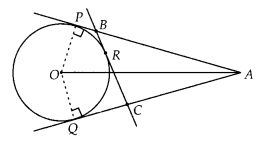

OP ⊥ AP
∴ ∠OPA = 90°
[Tangent at any point of a circle is perpendicular to the radius through the point of contact]
In ∆OAP,
OA² = OP² + PA²
⇒ 13² = 5² + PA²
⇒ PA = 12 cm
Now, perimeter of ∆ABC = AB + BC + CA
= AB + BR + RC + CA
= (AB + BR) + (RC + CA)
= (AB + BP) + (CQ + CA)
[ ∵ BR = BP, RC = CQ i.e., tangents from external point to a circle are equal]
= AP + AQ
= 2AP [∵ AP = AQ]
= 2 x 12 = 24 cm
Hence, the perimeter of ∆ABC = 24 cm.