Chapter 7 Coordinate Geometry
Class 10th Maths NCERT Exemplar Solution
NCERT Exemplar Problems Class 10 Maths – Coordinate Geometry
Question
1:
The distance of the point P(2, 3) from the X-axis is
(a)
2
(b)
3
(c)
1
(d) 5
(b)
We know that, if (x, y) is any point on the cartesian plane in first
quadrant.
Then, x = Perpendicular distance from Y-axis
and y =
Perpendicular distance from X-axis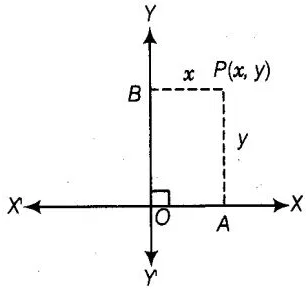
Distance of the
point P(2, 3) from the X-axis = Ordinate of a point P(2, 3)= 3.
Question
2:
The distance between the points A(0, 6) and 5(0,- 2)
is
(a)
6
(b)
8
(c)
4
(d) 2
Solution:
(b)
v Distance between the points (x1, y1) and (x2,
y2),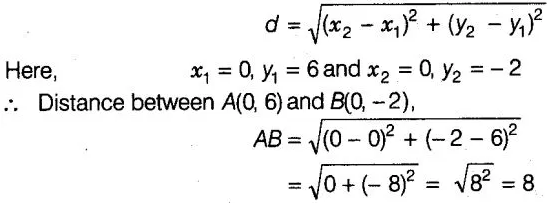
Question
3:
The distance of the point P(- 6, 8) from the origin is
(a)
8
(b)
2√7
(c)
10
(d) 6
Solution:
(c)
∴Distance between the points (x1,y2)and (x2,
y2)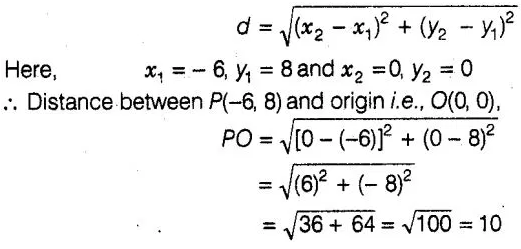
Question
4:
The distance between the points (0, 5) and (- 5, 0) is
(a)
5
(b)
5√2
(c)2√5
(d) 10
Solution:
(b)
∴ Distance between the points (x1,y1) and (x2,
y2),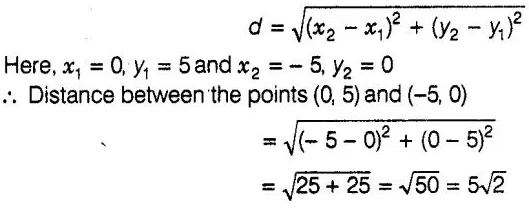
Question
5:
If AOBC is a rectangle whose three vertices are A(0, 3),
O(0, 0) and B(5, 0), then the length of its diagonal is
(a)
5
(b)
3
(c)
√34
(d) 4
Solution:
(c)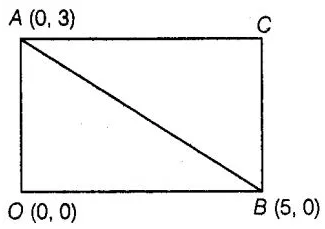
Now, length of the
diagonal AB = Distance between the points A(0, 3) and B(5, 0).
∴ Distance
between the points (x,, y,) and (x2, y2),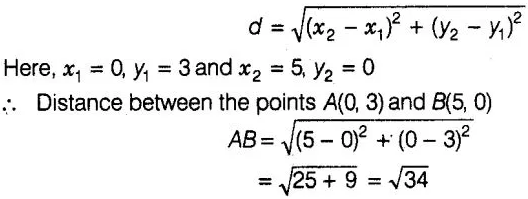
Hence, the required
length of its diagonal is √34.
Question
6:
The perimeter of a triangle with vertices (0, 4), (0, 0)
and (3, 0) is
(a)
5
(b)
12
(c)11
(d)7+√5
Solution:
(b)
we Further, adding all the distance of a triangle to get the perimeter
of a triangle.We plot the vertices of a triangle i.e., (0, 4), (0,0) and (3,0)
on the paper shown as given below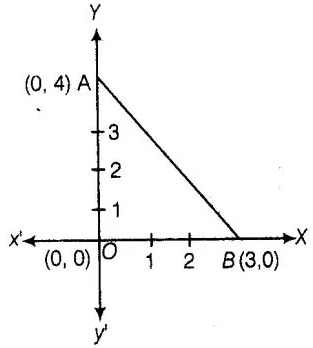
Now,perimeter of
ΔAOB=Sum of the length of all its sides = d(AO) + d(OB) + d(AB)
∴ Distance
between the points (x1,y1) and (x2,
y2),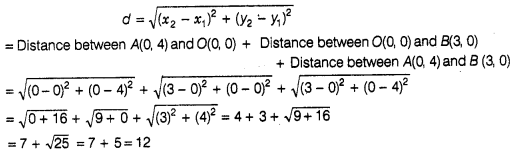
Hence, the required
perimeter of triangle is 12.
Question
7:
The area of a triangle with vertices A(3,0), B(7, 0) and
C(8, 4) is
(a)
14
(b)
28
(c)
8
(d) 6
Solution:
(c)
Area of Δ ABC whose Vertices
A≡(x1,y1),B≡(x2,y2) and
C≡(x3, y3) are given by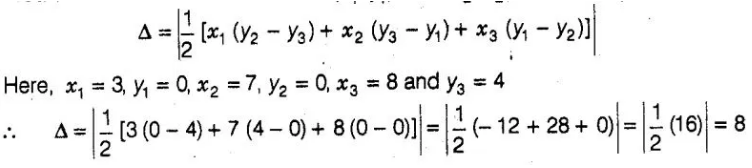
Hence, the required
area of AABC is 8.
Question
8:
The points (- 4, 0), (4, 0) and (0, 3) are the vertices of
a
(a) right angled
triangle
(b) isosceles triangle
(c) equilateral
triangle
(d) scalene triangle
Solution:
(b) Let A(-
4, 0), B(4, 0), C(0, 3) are the given vertices.
Now, distance between A (-4,
0) and B (4, 0),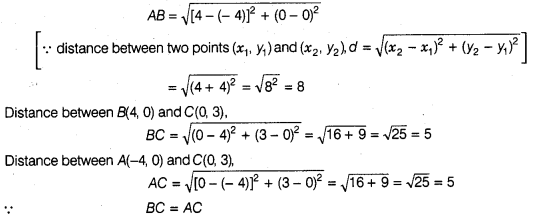
Hence, ΔABC is an
isosceles triangle because an isosceles triangle has two sides equal.
Question
9:
The point which divides the line segment joining the
points (7, – 6) and (3, 4) in ratio 1: 2 internally lies in the
(a) I
quadrant
(b) II
quadrant
(c) III
quadrant
(d) IV quadrant
Solution:
(d)
If P(x, y) divides the line segment joining A(x1,y2) and
B(x2, y2) internally in the ratio
Question
10:
The point which lies on the perpendicular bisector of the
line segment joining the points A(-2, – 5) and B(2, 5) is
(a)
(0,0)
(b) (0,
2)
(c) (2,
0)
(d)(-2,0)
Solution:
(a)
We know that, the perpendicular bisector of the any line segment divides
the^jjpe segment into two equal parts i.e., the perpendicular bisector of the
line segment always passes through the mid-point of the line segment.
Mid-point of the line segment joining the points A (-2, -5) and S(2, 5)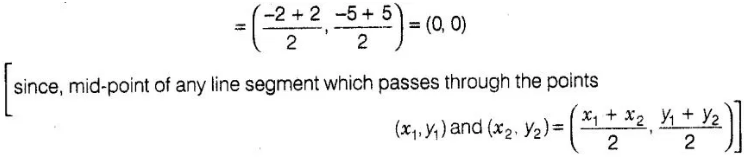
Hence, (0, 0) is the
required point lies on the perpendicular bisector of the lines segment.
Question
11:
The fourth vertex D of a parallelogram ABCD whose three
vertices are A(- 2, 3), B(6, 7) and C(8, 3) is
(a)
(0,1)
(b)
(0,-1)
(c)
(-1,0)
(d) (1,0)
Solution:
(b)
Let the fourth vertex of parallelogram, D≡(x4
,y4) and L, M be the middle points of AC and BD,
respectively,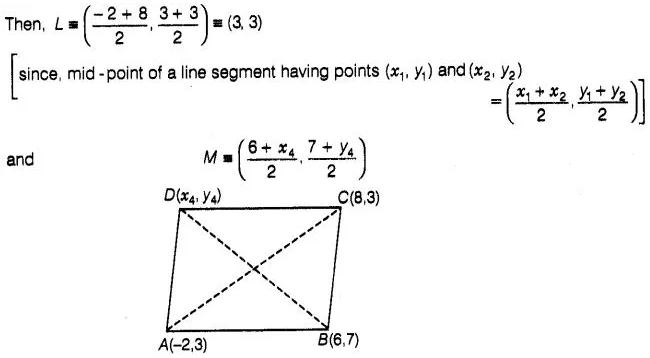
Since, ABCD is a
parallelogram, therefore diagonals AC and BD will bisect each other. Hence, L
and M are the same points.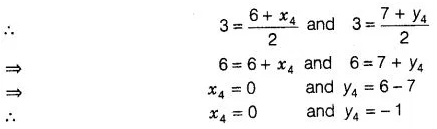
Hence, the fourth
vertex of parallelogram is D s (x4, y4) s (0,-1).
Question
12:
If the point P(2,1) lies on the line segment joining
points A(4, 2) and 6(8, 4), then
(a)AP = \(\frac { 1 }{ 3 }
\)AB
(b) AP =
PB
(c)PB = \(\frac { 1 }{ 3 }
\)AB
(d)AP = \(\frac { 1 }{ 2 } \)AB
Solution:
(d)
Given that, the point P(2,1) lies on the line segment joining the points A(4,2)
and 8(8, 4), which shows in the figure below: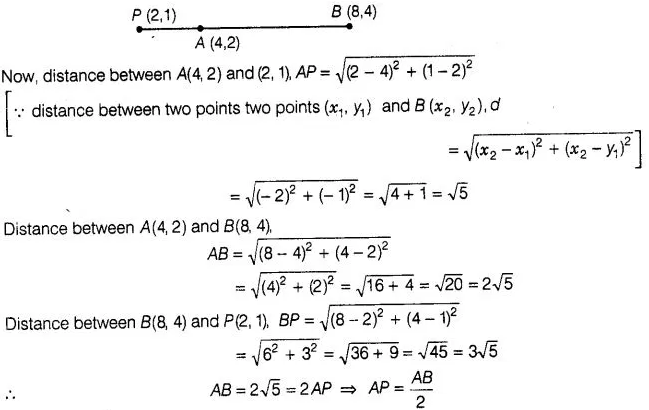
Hence, required
condition is AP = \(\frac { AB }{ 2 } \)
Question
13:
If P(\(\frac { 1 }{ 2 } \),4) is the mid-point of the
line segment joining the points Q(- 6, 5) and fl(- 2, 3), then
the value of a is
(a)-4
(b)
-12
(c)
12
(d) -6
Solution:
(b)
Given that, P(\(\frac { 1 }{ 2 } \),4) is the mid-point of the line segment
joining the points Q(-6, 5) and
R (-2, 3), which shows in the figure given
below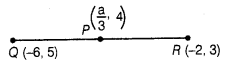
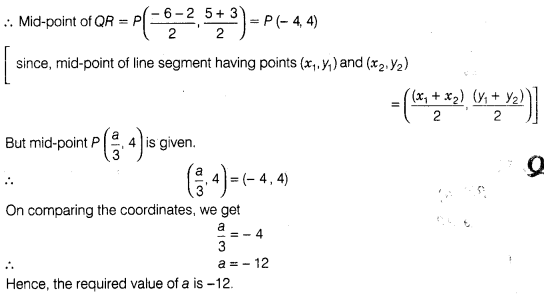
Hence, the required
value of a is -12.
Question
14:
The perpendicular bisector of the line segment joining
the points A(1,5) and 8(4,6) cuts the y-axis at
(a)
(0,13)
(b)
(0,-13)
(c)
(0,12)
(d) (13,0)
Solution:
(a)
Firstly, we plot the points of the line segment on the paper and join
them.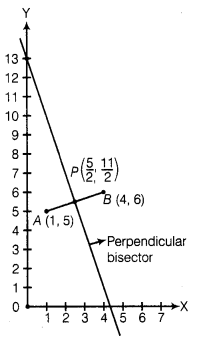
We know that, the
perpendicular bisector of the line segment AB bisect the segment AB, i.e.,
perpendicular bisector of line segment AB passes through the mid-point of
AB.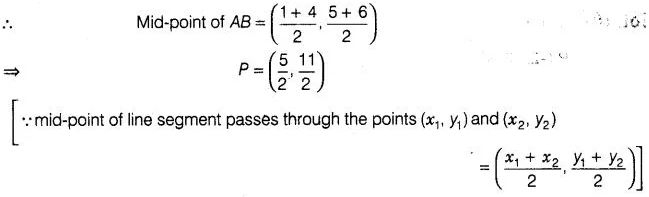
Now, we draw a straight
line on paper passes through the mid-point P. We see that the perpendicular
bisector cuts the Y-axis at the point (0,13).
Hence, the required point is
(0,13).
Alternate Method
We know that, the equation of
line which passes through the points (x1, y1) and
(x2, y2) is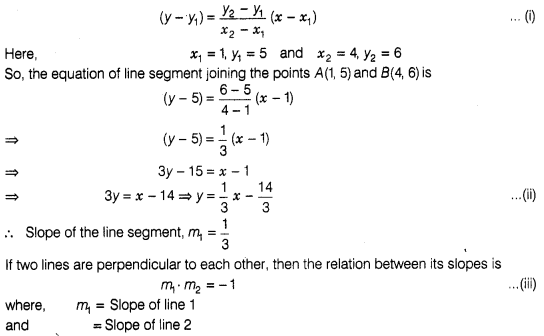
Also, we know that the
perpendicular bisector of the line segment is perpendicular on the line
segment.
Let slope of line segment is m2.
From Eq.
(iii),
So, the required point
is (0,13).
Question
15:
The coordinates of the point which is equidistant from
the three vertices of the ΔAOB as shown in the figure is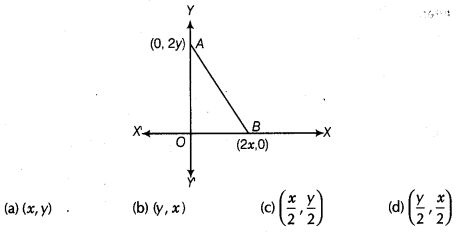
Solution:
(a)
Let the coordinate of the point which is equidistant from the three vertices
0(0, 0), A(0,2y) and B(2x, 0) is P(h,k).
Then,
PO = PA = PB
⇒
(PO)² = (PA)²=
(PB)2
… (i)
By distance formula,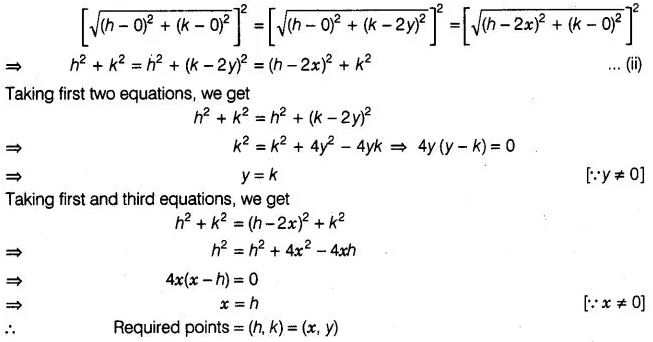
Question
16:
If a circle drawn with origin as the centre passes
through (\(\frac { 13 }{ 2 } \),0), then the point which does not lie in the
interior of the circle is![]()
Solution: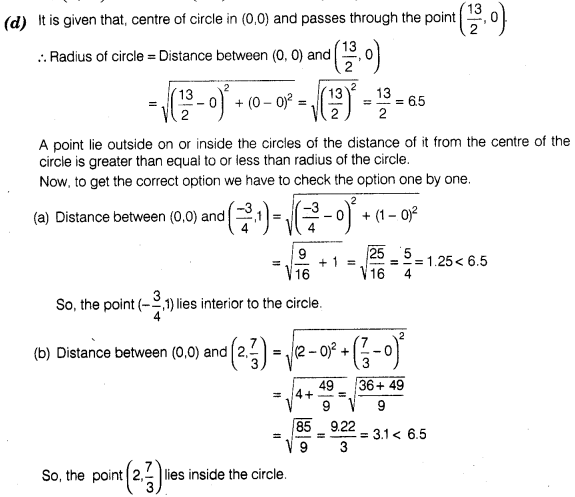

Question
17:
A line intersects the y-axis and X-axis at the points P
and Q, respectively. If (2, – 5) is the mid-point of PQ, then the coordinates of
P and Q are,
respectively
’
(a) (0,-5) and (2,
0)
(b) (0, 10) and (- 4, 0)
(c) (0, 4) and (- 10,
0)
(d) (0, – 10) and (4, 0)
Solution:
(d)
Let the coordinates of P and 0 (0, y) and (x, 0),
respectively.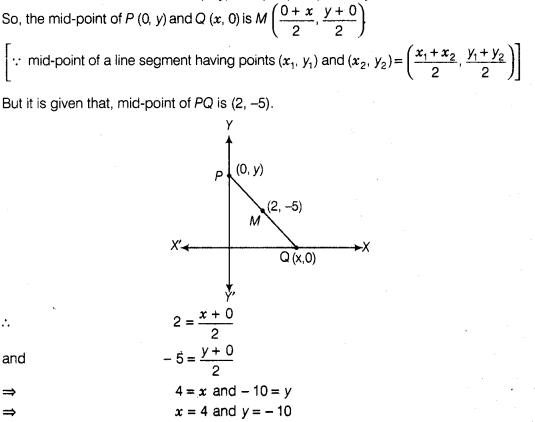
So, the coordinates of
P and Q are (0, -10) and (4, 0).
Question
18:
The area of a triangle with vertices (a, b + c) , (b, c +
a) and (c, a + b) is
(a) (a + b + c)²
(b) 0
(c) (a + b +
c)
(d) abc
Solution:
(b)
Let the vertices of a triangle are, A ≡ (x1, y1) ≡ (a, b +
c)
B ≡ (x2, y2) ≡ (b,c + a) and C = (x3,
y3) ≡ (c, a + b)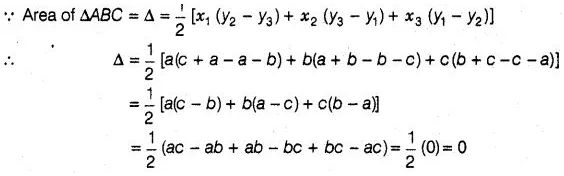
Hence, the required
area of triangle is. 0.
Question
19:
If the distance between the points (4, p) and (1, 0) is
5, then the value of pis
(a) 4
only
(b)
±4
(c) – 4
only
(d) 0
Solution:
(b)
According to the question, the distance between the points (4, p) and (1, 0) =
5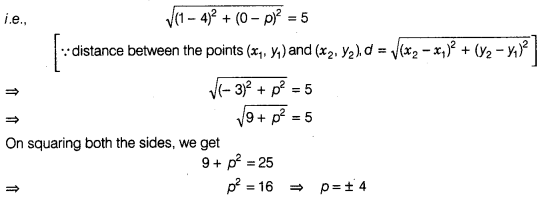
Hence, the required
value of p is ± 4,
Question
20:
If the points A(1, 2), B(0, 0) and C(a, b) are collinear,
then
(a) a =
b
(b) a =
2b
(c) 2a =
b
(d) a = – b
Solution:
(c)
Let the given points are B = (x1,y1) =
(1,2),
B = (x2,y2) = (0,0) and C3 =
(x3,y3)= (a, b).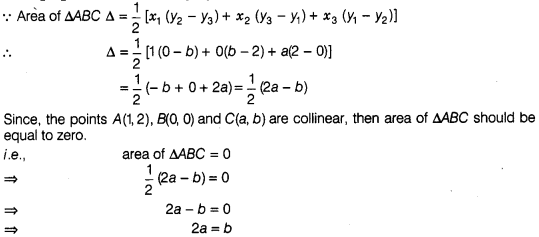
Hence, the required
relation is 2a = b.
Question
1:
Δ ABC with vertices A(0 ,- 2,0), B(2, 0) and C(0,2) is
similar to ΔDEF with vertices D (- 4, 0), E(4, 0) and F(0, 4).
Solution:
True
Hence, both the
triangles are similar.
[by SSS rule]
Question
2:
The point P(- 4, 2) lies on the line segment joining the
points A(- 4, 6) and B(- 4, – 6).
Solution:
True
We
plot all the points P(-4,2), A(-4, 6) and B(-4, – 6) on the graph
paper,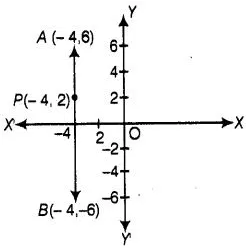
From the figure, point
P(- 4,2) lies on the line segment joining the points A(- 4,6) and B(- 4, –
6),
Question
3:
The points (0, 5), (0, -9) and (3, 6) are
collinear.
Solution:
False
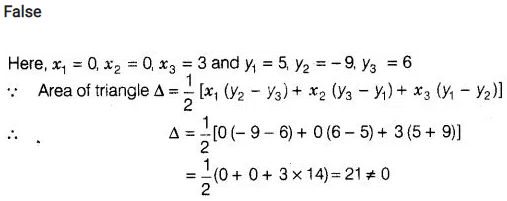
If the area of triangle
formed by the points (0, 5), (0 – 9) and (3, 6) is zero, then the points are
collinear.
Hence, the points are non-collinear.
Question
4:
Point P(0, 2) is the point of intersection of y-axis and
perpendicular bisector of line segment joining the points A(-l, 1) and B(3,
3).
Solution:
False
We
know that, the points lies on perpendicular bisector of the line segment joining
the two
points is equidistant from these two points.
Hence, the required
intersection point is (0, 4).
Question
5:
The points A(3,1), B(12, – 2) and C(0, 2) cannot be
vertices of a triangle.
Solution:
True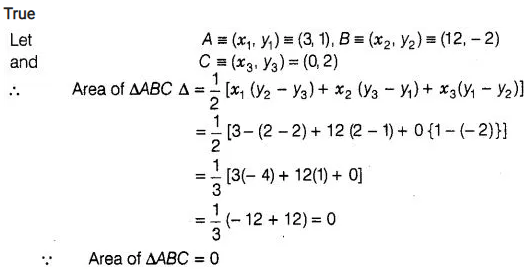
Hence, the points
A(3,1), B(12, -2) and C(0,2) are collinear.
So, the points A(3,1), B(12, – 2)
and C(0,2) cannot be the vertices of a triangle.
Question
6:
The points A(4, 3), B(6, 4), C(5, – 6) and D(- 3, 5) are
vertices of a parallelogram.
Solution:
False
In parallelogram,
opposite sides are equal. Here, we see that all sides AB, BC, CD and DA are
different.
Hence, given vertices are not the vertices of a parallelogram.
Question
7:
A circle has its centre at the origin and a point P (5, 0)
lies on it. The point Q (6, 8) lies outside the circle.
Solution:
True
First,we draw a circle and a point from the given information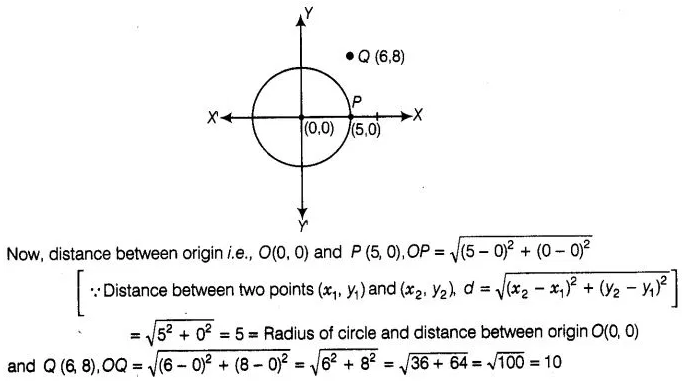
We know that, if the
distance of any point from the centre is less than/equal to/ more than the
radius, then the point is inside/on/outside the circle, respectively.
Here,
we see that, OQ > OP
Hence, it is true that point Q (6, 8), lies outside
the circle.
Question
8:
The point A (2, 7) lies on the perpendicular bisector of
the line segment joining the points P (5, – 3) and Q (0, – 4).
Solution:
False
If
A (2,7) lies on perpendicular bisector of P(6,5) and Q (0, – 4), then
AP=AQ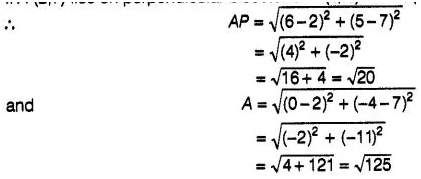
So, A does not lies on
the perpendicular bisector of PQ.
Alternate Method
If the
point A (2,7) lies on the perpendicular bisector of the line segment, then the
point A satisfy the equation of perpendicular bisector.
Now, we find the
equation of perpendicular bisector. For this, we find the slope of perpendicular
bisector.
Hence, the point A
(2,7) does not lie on the perpendicular bisector of the line segment.
Question
9:
The point P(5, – 3) is one of the two points of trisection
of line segment joining the points A(7, – 2) and B(1, – 5).
Solution:
True
Let
P (5,-3) divides the line segment joining the points A (7,-2) and B (1 ,-5) in
the ratio k: 1 internally.
By section formula, the coordinate of point P will
be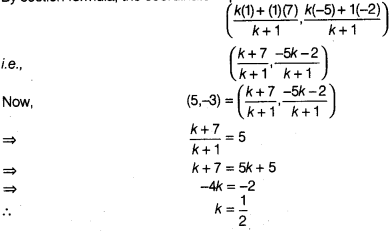
So the point P divides
the line segment AB in ratio 1: 2. Hence, point P in the point of trisection of
AB.
Question
10:
The points A (-6,10), B(- 4, 6) and C(3, -8) are
collinear such that
AB =\(\frac { 2 }{ 9 } \) AC.
Solution:
True
If the area of triangle formed by the points (x1,y2),
(x2, y2) and (x3, y3) is zero, then
the points are collinear,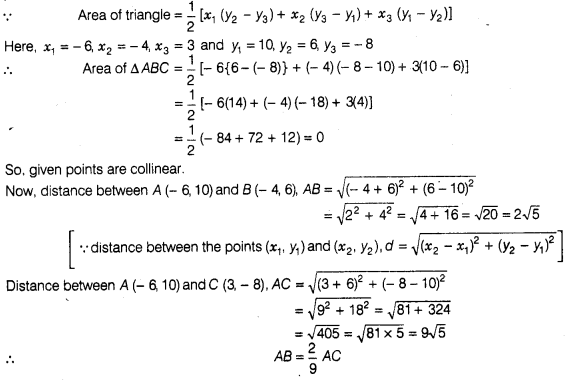
which is the required relation.
Question
11:
The point P(- 2, 4) lies on a circle of radius 6 and
centre (3, 5).
Solution:
False
If
the distance between the centre and any point is equal to the radius, then we
say that point lie on the circle.
Now, distance between P (-2,4) and centre
(3, 5)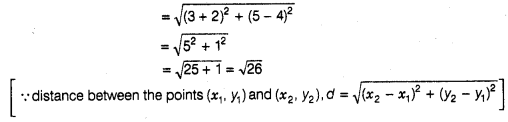
which is not equal to
the radius of the circle.
Hence, the point P(-2, 4) does not lies on the
circle.
Question
12:
The points A(- 1, – 2), B (4, 3), C (2, 5) and D (- 3, 0)
in that order form a rectangle.
Solution:
True
Since, diagonals AC and
BD are equal.
Hence, the points A (-1, – 2), B (4, 3), C (2, 5)and D (- 3
0)form a rectangle.
Question
1:
Name the type of triangle formed by the points A (-5, 6),
B(- 4, – 2) and C(7, 5).
Solution:
To find the
type of triangle, first we determine the length of all three sides and see
whatever condition of triangle is satisfy by these sides.
Now, using distance
formula between two points,
We see
that,
AB ≠ BC ≠ CA
and not hold the condition of Pythagoras in a ΔABC.
i.e.,
(Hypotenuse)2 =( Base)2 +
(Perpendicular)2
Hence, the required triangle is scalene because
all of its sides are not equal i.e., different to each other.
Question
2:
Find the points on the X-axis which are at a distance of
2√5 from the point (7, -4). How many such points are there?
Solution:
We
know that, every point on the X-axis in the form (x, 0). Let P(x, 0) the point
on the X-axis
have 2√5 distance from the point Q (7, – 4).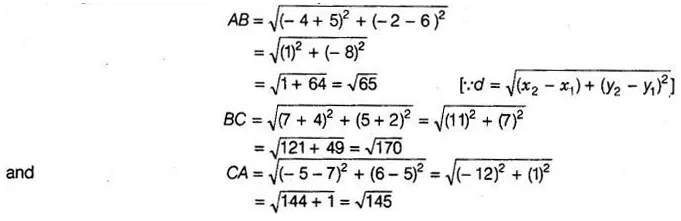
Hence, there are two
points lies on the axis, which are (5, 0) and (9, 0), have 2V5 distance from the
point (7, – 4).
Question
3:
What type of quadrilateral do the points A (2, -2), B (7,
3) C (11, – 1) and D (6, – 6) taken in that order form?
Solution:
To
find the type of quadrilateral, we find the length of all four sides as well as
two diagonals and see whatever condition of quadrilateral is satisfy by these
sides as well as diagonals. Now, using distance formula between two
points,
Here, we see that the
sides AB = CD and BC = DA
Also, diagonals are equal i.e., AC = BD
which
shows the quadrilateral is a rectangle.
Question
4:
Find the value of a, if the distance between the points
A(- 3, – 14) and B (a, – 5) is 9 units.
Solution:
According to
the question,
Distance between A (- 3, -14) and 8 (a, – 5), AB = 9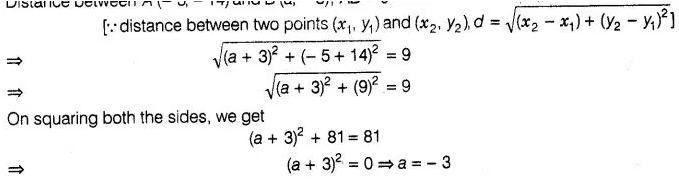
Hence, the required
value of a is – 3.
Question
5:
Find a point which is equidistant from the points A (- 5,
4) and B (- 1, 6). How many such points are there?
Solution:
Let
P (h, k) be the point which is equidistant from the points A (- 5, 4) and B (-1,
6).
So, the mid-point of AB
satisfy the Eq. (i). Hence, infinite number of points, in fact all points which
are solution of the equation 2h + k +1 = 0, are equidistant from the points A
and B.
Replacing h, k by x, y in above equation, we have 2 x +y+1= 0
Question
6:
Find the coordinates of the point Q on the x-axis which
lies on the perpendicular bisector of the line segment joining the points A (-
5, – 2) and B (4, – 2). Name the type of triangle formed by the point Q, A and
B.
Solution:
Firstly, we
plot the points of the line segment on the paper and join them.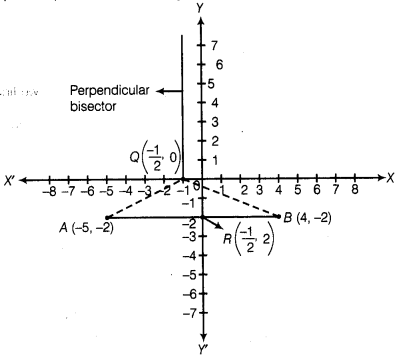
We know that, the
perpendicular bisector of the line segment AB bisect the segment AB,
i.e.,perpendicular bisector of the line segment AB passes through the mid-point
of AB.
Alternate
Method
•
(i) To find the coordinates of the point of 0 on the
X-axis. We find the equation of perpendicular bisector of the line segment
AS.
Now, slope of line segment AB,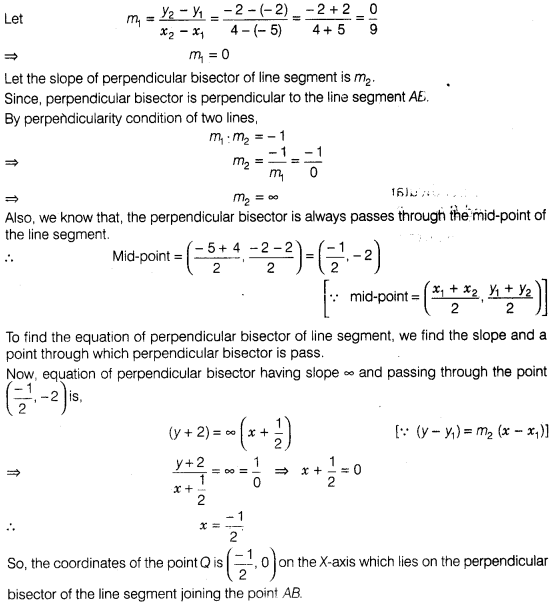
To know the type of
triangle formed by the points Q, A and B. We find the length of all three sides
and see whatever condition of triangle is satisfy by these sides.
Now, using
distance formula between two points,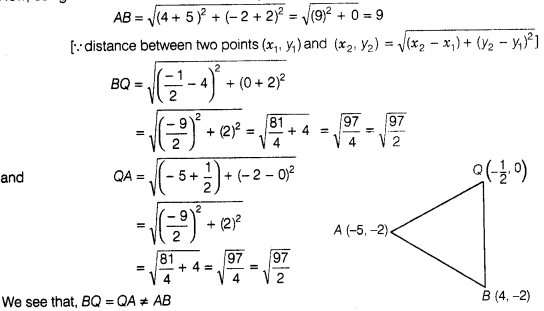
which shows that the
triangle formed by the points Q, A and 6 is an isosceles.
Question
7:
Find the value of m, if the points (5,1), (- 2, – 3) and
(8, 2m) are collinear.
Solution:
Let A ≡
(x1,y1) s (5,1), B = (x2, y2) = (-
2, – 3), C s (x3, y3) = (8,2m)
Since, the points A ≡
(5,1), B ≡ (- 2, – 3) and C ≡ (8,2m) are collinear.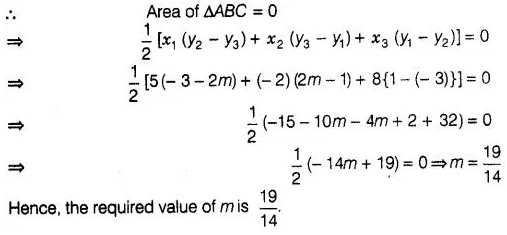
Question
8:
If the point A(2, – 4) is equidistant from P(3, 8) and Q(-
10, y), then find the value of y. Also, find distance PQ.
Solution:
According
to the question,
A (2, – 4) is equidistant from P (3, 8) = 0 (-10, y) is
equidistant from A (2, – 4)
Hence, the values of y
are -3, – 5 and corresponding values of PQ are √290 and √338 = 1342,
respectively.
Question
9:
Find the area of the triangle whose vertices are (-8,4),
(-6,6) and (- 3, 9).
Solution:
Given that,
the vertices of triangles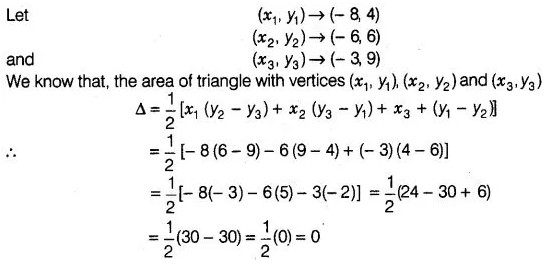
Hence, the required
area of triangle is 0.
Question
10:
In what ratio does the X-axis divide the line segment
joining the points (- 4, – 6) and (- 1, 7)? Find the coordinates of the points
of division.
Solution:
Let the
required ratio be λ: 1. So, the coordinates of the point M of division A (- 4, –
6) and B(-1,7) are
Question
11:
Find the ratio in which the point P(\(\frac { 3 }{ 4 }
\),\(\frac { 5 }{ 12 } \)) divides the line segment joinnig the points A(\(\frac
{ 1 }{ 2 } \),\(\frac { 3 }{ 2 } \)) and B(2,5).
Solution:
Let
P(\(\frac { 3 }{ 4 } \),\(\frac { 5 }{ 12 } \)) divide AB internally in the
ratio m:n
using the section formula ,we get

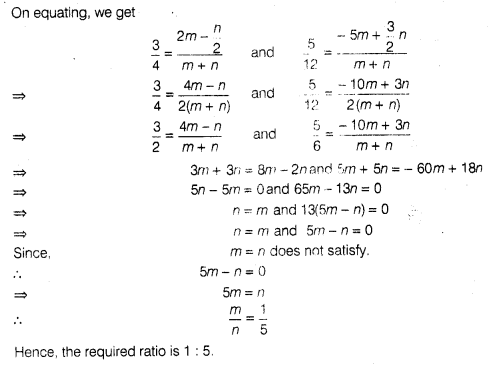
Hence, the required
ratio is 1 : 5.
Question
12:
If P(9a -2, – b) divides line segment joining A(3a +
1,-3) and B(8a, 5) in the ratio 3 : 1, then find the values of a and b.
Solution:
Let P(9a –
2, – b) divides AS internally in the ratio 3:1.
By section formula,
Hence, the required
values of a and b are 1 and – 3.
Question
13:
If (a, b) is the mid-point of the line segment joining
the points A(10, – 6), B(k, 4) and a – 2b= 18, then find the value of k and the
distance AB.
Solution:
Since, (a,
b) is the mid-point of line segment AB.
Hence, the required
distance of AB is 2√61.
Question
14:
If the centre of a circle is (2a, a – 7), then Find the
values of a, if the circle passes through the point (11, – 9) and has
diameter 10√2 units.
Solution:
By given
condition,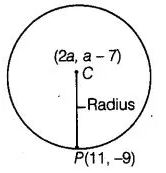
Distance between the
centre C(2a, a – 7) and the point P( 11, – 9), which lie on the circle = Radius
of circle
Hence, the required
values of a are 5 and 3.
Question
15:
The line segment joining the points A(3, 2) and B(5,1) is
divided at the point P in the ratio 1 : 2 and it lies on the line
3x – 18y +
k = 0. Find the value of k.
Solution:
Given that,
the line segment joining the points 4(3,2) and 6(5,1) is divided at the point P
in the ratio 1 : 2.
Hence, the required
value of k is 19.
Question
16:
If D(\(\frac { -1 }{ 2 } \),\(\frac { 5 }{ 2 } \)) E(7,3)
and F(\(\frac { 7 }{ 2 } \),\(\frac { 7 }{ 2 } \)) are the mid-points of
sides of ΔABC,then find the area of the ΔABC.
Solution:
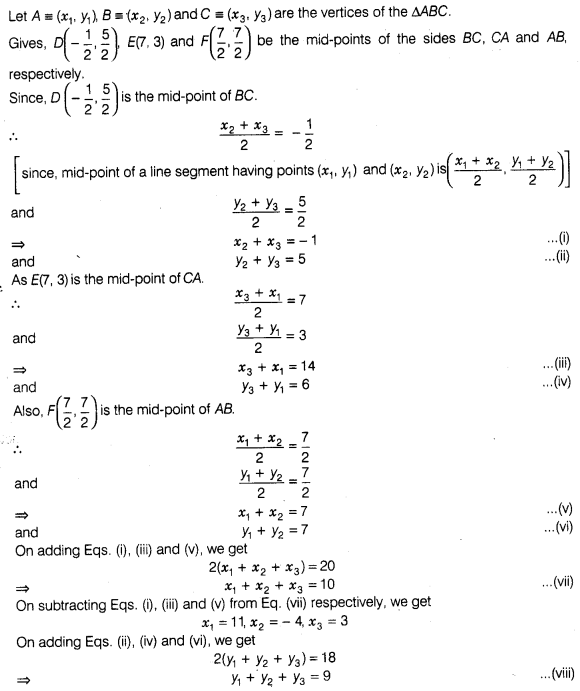

Question
17:
If the points A (2, 9), B (a, 5) and C (5, 5) are the
vertices of a ABC right angled at B, then find the values of a and hence the
area of ΔABC.
Solution:
Given that,
the points A (2, 9), B(a, 5) and C(5, 5) are the vertices of a ΔABC right angled
at B.
By Pythagoras theorem, AC2 = AB2 +
BC2
,,.(i)
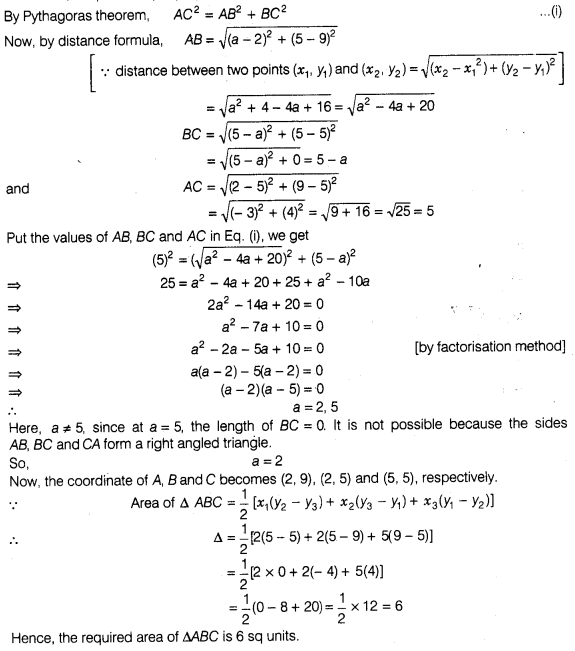
Hence, the required
area of ΔABC is 6 sq units.
Question
18:
Find the coordinates of the point R on the line segment
joining the points P(- 1, 3) and Q(2, 5) such that
PR = \(\frac { 3 }{ 5 } \)
PQ.
Solution:
According to
the question,
Question
19:
Find the values of k, if the points A(k + 1, 2k), B(3k,
2k + 3) and C (5k – 1, 5k) are colli near.
Solution:
We
know that, if three points are collinear, then the area of triangle formed by
these points is zero.
Since, the points A(k + 1,2k), B(3k, 2k + 3) and C(5k
-1, 5k) are collinear.
Then, area of ΔABC = 0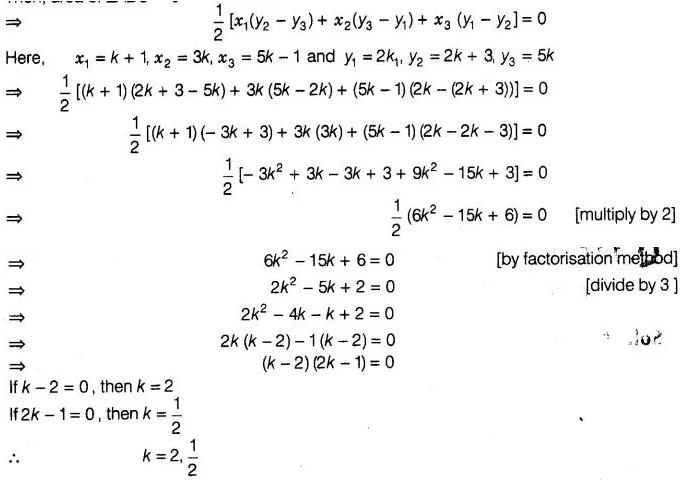
Hence, the required
values of k are 2 and \(\frac { 1 }{ 2 }\)
Question
20:
Find the ratio in which the line 2x+ 3y – 5 = 0 divides
the line segment joining the points (8, – 9) and (2,1). Also, find the
coordinates of the point of division.
Solution:
Let the line
2x + 3y – 5 = 0 divides the line segment joining the points A (8, – 9) and B
(2,1) in the ratio λ: 1 at point P.
Question
1:
If (- 4, 3) and (4, 3) are two vertices of an equilateral
triangle, then find the coordinates of the third vertex, given that the origin
lies in the interior of the triangle.
Solution:
Let the
third vertex of an equilateral triangle be (x, y). Let A (- 4, 3), B(4 3) and C
(x, y).
We know that, in equilateral triangle the angle between two adjacent
side is 60 and all three sides are equal.
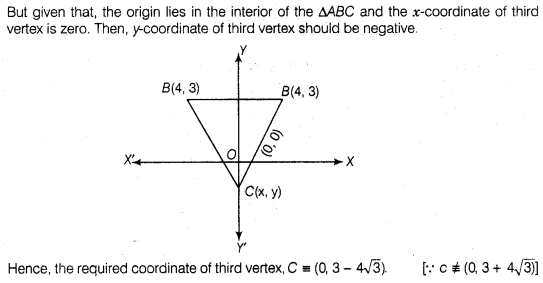
Question
2:
A(6,1), B (8, 2) and C(9, 4) are three vertices of a
parallelogram ABCD. If E is the mid-point of DC, then find the area of
ΔADE.
Solution:
Given that,
A (6,1), B (8,2) and C (9, 4) are three vertices of a parallelogram ABCD.
Let
the fourth vertex of parallelogram be (x, y).
We know that, the diagonals of
a parallelogram bisect each other.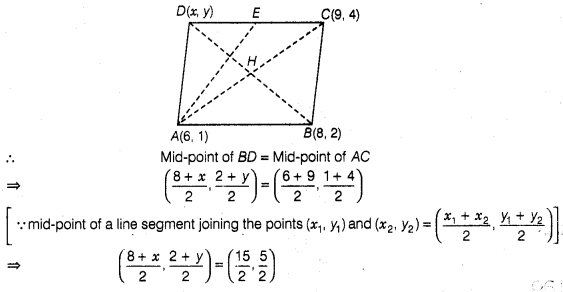
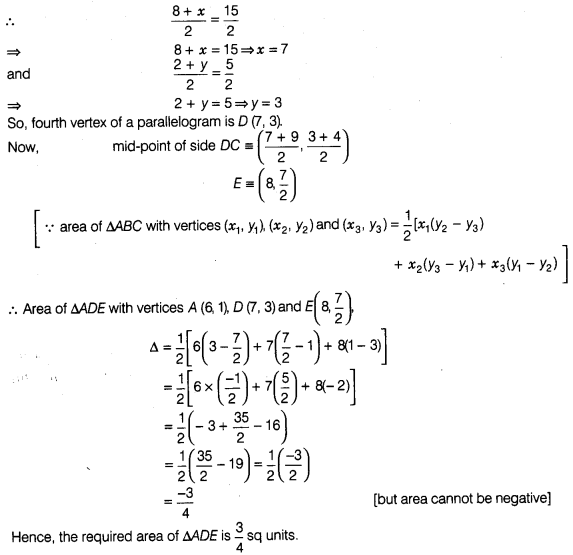
Hence, the required
area of ΔADE is \(\frac { 3 }{ 4 }\) sq units.
Question
3:
The points A(x1, y1),
B(x2 y2) and C(x3, y3) are the
vertices of ΔABC.
(i) The median from A meets BC at Find the
coordinates of the point D.
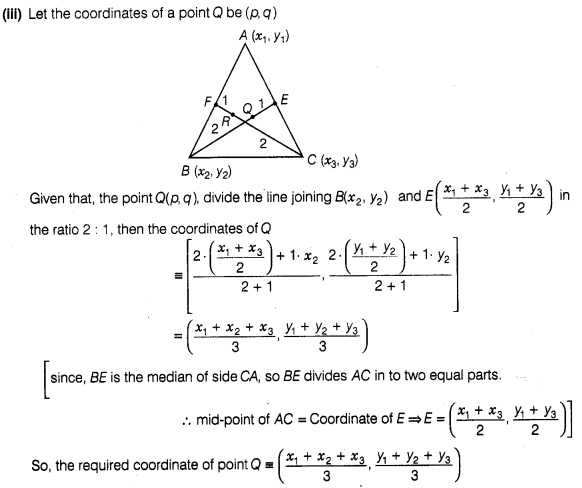
(ii) Find the coordinates of the point P on
AD such that AP : PD = 2:1
(iii) Find the coordinates of points Q and R on
medians BE and CF, respectively such that BQ:QE = 2:1 and CR:RF = 2:1
(iv )
What are the coordinates of the centroid of the ΔABC?
Solution:
Given
that, the points A (x1, y1), B(x2,
y2)andC (x3, y3)are the vertices of
ΔABC.
(i) We know that, the median bisect the line segment
into two equal parts i.e., here D is the mid-point of BC.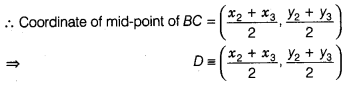


Question
4:
If the points A (1, – 2), B (2, 3), C(a, 2) and D(- 4, –
3) form a parallelogram, then find the value of a and height of the
parallelogram taking AB as base.
Solution:
In
parallelogram, we know that, diagonals are bisects each other i.e., mid-point of
AC = mid-point of BD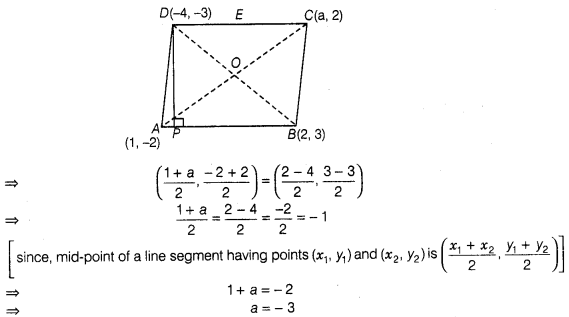
So, the required value
of a is – 3.
Given that, AS as base of a parallelogram and drawn a
perpendicular from D to AS which meet AS at P. So, DP is a height of a
parallelogram.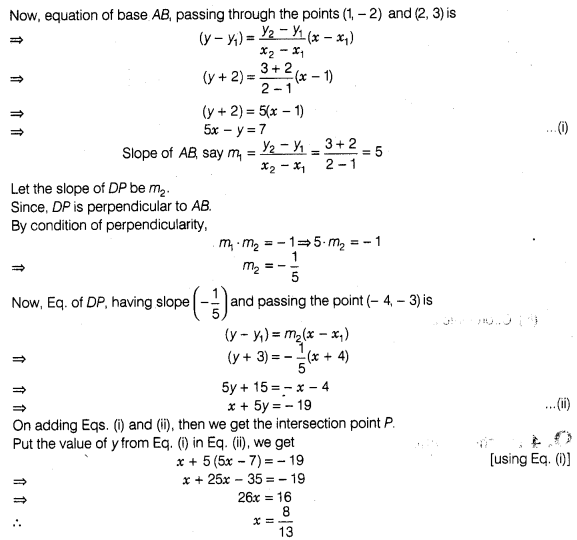

Question
5:
Students of a school are standing in rows and columns in
their playground for a drill practice. A, B, C and D are the positions of four
students as shown in figure. Is it possible to place Jaspal in the drill in such
a way that he is equidistant from each of the four students A, B, C and D? If
so, what should be his position?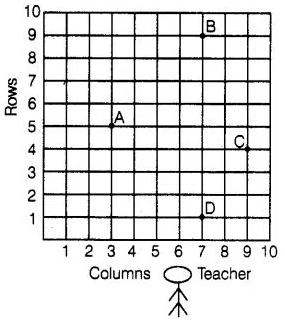
Solution:
Yes,
from the figure we observe that the positions of four students A, B, C and D are
(3, 5), (7, 9), (11, 5) and (7,1) respectively i.e., these are four vertices of
a quadrilateral. Now, we will find the type of this quadrilateral. For this, we
will find all its sides.
We see that, AB = BC = CD = DA i.e., all sides are
equal.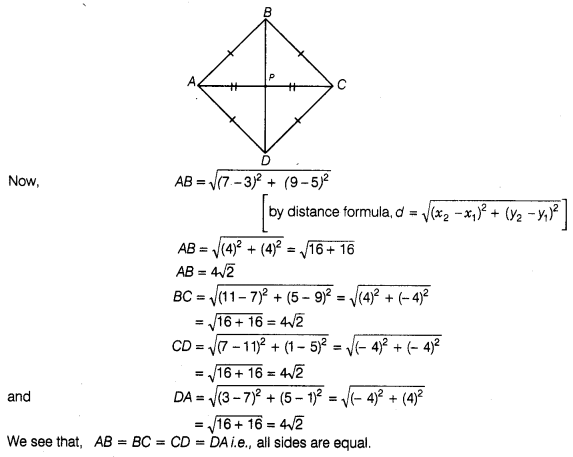

Hence, the required
position of Jaspal is (7, 5).
Question
6:
Ayush starts walking from his house to office. Instead of
going to the office directly, he goes to a bank first, from there to his
daughter’s school and then reaches the office. What is the extra distance
travelled by Ayush in reaching his office? (Assume that all distance covered are
in straight lines). If the house is situated at (2, 4), bank at (5, 8), school
at (13,14) and office at (13, 26) and coordinates are in km.
Solution:
So, extra distance
travelled by Ayush in reaching his office = 27 – 24.6 = 2.4 km Hence, the
required extra distance travelled by Ayush is 2.4 km.