Chapter 4 Quadratic Equations

NCERT Exemplar Class 10 Maths Chapter 4 Quadratic Equations

Exercise 4.1

Choose the correct answer from the given four options in the following questions:

Question 1
Which of the following is a quadratic equation?
(A) x² + 2x + 1 = (4 – x)² + 3
(B) -2x² = (5 – x) (2x – \(\frac { 2 }{ 5 }\) )
(C) (k+ 1)x² + \(\frac { 3 }{ 2 }\) x = 7,where k = -1
(D) x³ – x²= (x – 1 )³
Solution:
(D)
(A) Given equation is, x² + 2x + 1 = (4 – x)² + 3
⇒ x² + 2x + 1 = 16 + x² – 8x + 3
⇒ 10x – 18 = 0
which is not of the form ax² + bx + c, a ≠ 0. Thus, the equation is not a quadratic equation.

(B) Given equation is -2x² = (5 – x) (2x – \(\frac { 2 }{ 5 }\) )
⇒ -2x² = 10x – 2x² – 2 + \(\frac { 2x }{ 5 }\)
⇒ 0 = 10x – 2 + \(\frac { 2x }{ 5 }\)
⇒ 50x + 2x – 10 = 0
⇒ 52x – 10 = 0
which is also not a quadratic equation.

(C) Given equation is, x²(k +1) + \(\frac { 3 }{ 2 }\) x = 7
∵ k = -1 [Given]
⇒ x2(-1 + 1) + \(\frac { 3 }{ 2 }\)x = 7
⇒ \(\frac { 3 }{ 2 }\)x = 7
⇒ 3x – 14 = 0
which is also not a quadratic equation.

(D) Given equation is, x³ – x² = (x – 1)³
⇒ x³ – x² = x³ – 3x²(1) + 3x(1)² – (1)³
[ ∵(a – b)³ = a³ -b³+ 3ab² – 3a²b]
⇒ x³ – x² = x³– 3x² + 3x – 1
⇒ -x² + 3x² – 3x + 1 = 0
⇒ 2x² – 3x + 1 = 0
which represents a quadratic equation because it is of the quadratic form ax² + bx + c = 0, a ≠ 0.

Question 2
Which of the following is not a quadratic equation?
(A) 2(x – 1 )² = 4x² – 2x + 1
(B) 2x – x² = x² + 5
(C) (√2x + √3)²+ x²= 3x² – 5x
(D) (x² + 2x)² = x⁴+ 3 + 4x³
Solution:
(C) (A) Given that,
2(x – 1)² = 4x² – 2x + 1
⇒ 2(x² + 1 – 2x) = 4x² – 2x + 1
⇒ 2x² + 2 – 4x = 4x² – 2x + 1
⇒ 2x² + 2x – 1 = 0
which represents a quadratic equation because it is of the quadratic form ax² + bx + c = 0, a ≠ 0.

(B) Given that, 2x – x² = x² + 5
⇒ 2x² – 2x + 5 = 0
which also represents a quadratic equation because it is of the quadratic form ax² + bx + c = 0, a ≠ 0.

(C) Given that, (√2x + √3)² + x² = 3x² – 5x
⇒ 2x² + 3 + 2√6x + x² = 3x² – 5x
⇒ (5 + 2√6)x + 3 = 0
which does not represent a quadratic equation because it is not of the quadratic form ax² + bx + c = 0, a ≠ 0.

(D) Given that,
(x² + 2x)² = x⁴ + 3 + 4x³
⇒ x⁴ + 4x² + 4x³ = x⁴ + 3 + 4x³
⇒ 4x² – 3 = 0
which represents a quadratic equation because it is of the quadratic form ax²+ bx + c = 0, a ≠ 0

Question 3
Which of the following equations has 2 as a root?
(A) x² – 4x + 5 = 0
(B) x² + 3x – 12 = 0
(C) 2x² – 7x + 6 = 0
(D) 3x² – 6x – 2 = 0
Solution:
(C)
(A) Substituting x = 2 in x² – 4x + 5, we get
(2)² – 4(2) + 5 = 4 – 8 + 5 = 1 ≠ 0
So, x = 2 is not a root of x² – 4x + 5 = 0

(B) Substituting x = 2 in x² + 3x – 12 we get
(2)² + 3(2) -12 = 4 + 6-12 = -2 ≠ 0
So, x = 2 is not a root of x² + 3x -12 = 0

(C) Substituting x = 2 in 2x² – 7x + 6, we get 2(2)² – 7(2) + 6
= 8 – 14 + 6 = 14 – 14 = 0
So, x = 2 is a root of 2x² – 7x + 6 = 0

(D) Substituting x = 2 in 3x² – 6x -2, we get
3(2)² – 6(2) – 2 = 12 – 12 – 2 = -2 ≠ 0
So, x = 2 is not a root of 3x² – 6x – 2 = 0

Question 4
If \(\frac { 1 }{ 2 }\) is a root of the equation x² + kx – \(\frac { 5 }{ 4 }\) = 0, then the value of k is
(A) 2
(B) -2
(C) \(\frac { 1 }{ 4 }\)
(D) \(\frac { 1 }{ 2 }\)
Solution:
(A) Since, \(\frac { 1 }{ 2 }\) is a root of the quadratic equation x² + kx – \(\frac { 5 }{ 4 }\) = 0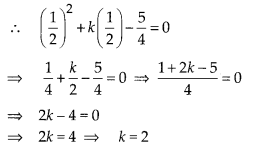

Question 5
Which of the following equations has the sum of its roots as 3?
(A) 2x² – 3x + 6 = 0
(B) -x² + 3x – 3 = 0
(C) √2x² – 3/√2x + 1 = 0
(D) 3x² – 3x + 3 = 0
Solution:
(B)
(A) Given equation is, 2x² – 3x + 6 = 0
On comparing with ax² + bx + c = 0, we get
a = 2, b = -3 and c = 6
∴ Sum of the roots = \(\frac { -b }{ a }\) = \(\frac { -(-3) }{ 2 }\) = \(\frac { 3 }{ 2 }\)
Therefore, sum of the roots of the quadratic equation 2x² – 3x + 6 = 0 is not 3.

(B) Given equation is -x² + 3x -3 = 0
On comparing with ax² + bx + c = 0, we get
a = -1, b = 3 and c = -3
∴ Sum of the roots = \(\frac { -b }{ a }\) = \(\frac { -3 }{ -1 }\) = 3
Therefore, sum of the roots of the quadratic equation -x²+ 3x – 3 = 0 is 3.

(C) Given that, √2x² – 3/√2x + 1 = 0
⇒ 2x² – 3x + √2=0
On comparing with ax² + bx + c = 0,
we get a = 2, b = -3 and c = √2
∴ Sum ot the roots = \(\frac { -b }{ a }\) = \(\frac { -(-3) }{ 2 }\) = \(\frac { 3 }{ 2 }\)
Therefore, sum of the roots of the quadratic equation √2x² – 3/√2x + 1 = 0 is not 3.

(D) Given that, 3x² – 3x + 3 = 0
⇒ x² – x + 1 = 0
On comparing with ax² + bx + c = 0,
we get a = 1, b = -1 and c = 1
∴ Sum of the roots = \(\frac { -b }{ a }\) = \(\frac { -(-1) }{ 1 }\) = 1
Therefore, sum of the roots of the quadratic equation 3x² – 3x + 3 = 0 is not 3.

Question 6
Values of k for which the quadratic equation 2x² -kx + k = 0 has equal roots is
(A) Oonly
(B) 4
(C) 8 only
(D) 0,8
Solution:
(D) Given equation is 2x² – kx + k = 0
On comparing with ax² + bx + c = 0, we get
a = 2,b = -k and c = k
For equal roots, the discriminant must be zero
i.e., D = b² – 4ac = 0
⇒ (-k)² – 4(2)k = 0
⇒ k² – 8k = 0
⇒ k(k – 8) = 0
∴ k = 0, 8
Hence, the required values of k are 0 and 8.

Question 7
Which constant must be added and subtracted to solve the quadratic equation 9x² + \(\frac { 3 }{ 4 }\) x – √2 = 0 by the method of completing the square?

Solution:
(B) Given equation is
9x² + \(\frac { 3 }{ 4 }\) x – √2 = 0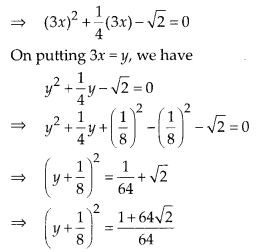

Thus, \(\frac { 1 }{ 64 }\) must be added and subtracted to solve the given equation.

Question 8
The quadratic equation 2x² – √5x + 1 = 0 has
(A) two distinct real roots
(B) two equal real roots
(C) no real roots
(D) more than 2 real roots
Solution:
(C) Given equation is 2x² – √5x + 1 = 0
On comparing with ax² + bx + c = 0, we get
a = 2 ,b = -77 and c = 1
D = b2 – 4ac = (-√5)² – 4 x (2) x (1) = 5 – 8
= -3 < 0
Since, discriminant is negative, therefore quadratic equation 2x² – √5x + 1 = 0 has no real roots.

Question 9
Which of the following equations has two distinct real roots?
(A) 2x² – 3√2x + \(\frac { 9 }{ 4 }\) = 0
(B) x² + x – 5 = 0
(C) x² + 3x + 2√2 = 0
(D) 5x² – 3x + 1 = 0
Solution:
(B)
(A) Given equation is
2x² – 3√2x + \(\frac { 9 }{ 4 }\) = 0
On comparing with ax² + bx + c = 0, we get
a = 2, b= 3√2 and c = \(\frac { 9 }{ 4 }\)
∴ D = b² – 4ac = (-3√2)2 – 4(2) (\(\frac { 9 }{ 4 }\))
= 18 – 18 = 0
So, the equation has real and equal roots.

(B) Given equation is x² + x – 5 = 0
On comparing with ax² + bx + c = 0, we get
a = 1, b = 1 and c = -5
∴D = b²– 4ac = (1)² – 4(1) (-5) = 1 + 20 = 21
⇒ b² – 4ac > 0
So, the equation has two distinct real roots.

(C) Given equation is x² + 3x + 2√2 = 0
On comparing with ax² + bx + c = 0, we get
a = 1, b = 3 and c = 2√2
∴ D = b² – 4ac = (3)² – 4(1)(2√2 )
= 9 – 8√2 < 0
So, roots of the equation are not real.

(D) Given equation is 5x² – 3x + 1 = 0
On comparing with ax² + bx + c = 0, we get
a = 5,b = -3 and c = 1
∴ D = b² – 4ac = (-3)² -4(5)(1)
= 9 – 20 = -ll<0
So, roots of the equation are not real.

Question 10
Which of the following equations has no real roots?
(A) x² – 4x + 3√2 =0
(B) x² + 4x – 3√2 =0
(C) x² – 4x – 3√2 =0
(D) 3x² + 4√3x + 4 = 0
Solution:
(A)
(A) given equation is x² – 4x + 3√2 =0
On comparing with ax² + bx + c – 0, we get
a = 1, b = -4 and c = 3√2
The discriminant of x² – 4x + 3√2 = 0 is
D = b²– 4ac
= (-4)²– 4(1)(3√2)
= 16 – 12√2
= 16 – 12 x (1.41)
= 16 – 16.92
= -0.92
∵ b² – 4ac<0
∴ Roots of the equation are not real.

(B) Given equation is x² + 4x – 3√2 = 0
On comparing with ax² + bx + c = 0,
we get
a = 1,b = 4 and c = -3√2
∴ D = b² – 4ac = (4)² – 4(1)(-3√2)
= 16 + 12√2 >0
Hence, the equation has real roots.

(C) Given equation is x² – 4x – 3√2 = 0
On comparing with ax² + bx + c = 0,
we get a = 1, b = -4 and c = -3√2
∴ D = b² – 4ac = (-4)² – 4(1)(-3√2)
= 16 + 12√2 >0
Hence, the equation has real roots.

(D) Given equation is 3x² + 4√3x + 4 = 0
On comparing with ax² + bx + c = 0, we get
a = 3,b = 4√3 and c = 4
∴ D = b² – 4ac = (4√3 )² – 4(3)(4)
= 48 – 48 = 0
Hence, the equation has real and equal roots.

Question 11
(x² + 1 )² – x² = 0 has
(A) four real roots
(B) two real roots
(C) no real roots
(D) one real root.
Solution:
(C) Given equation is (x² + 1)² – x² = 0
⇒ x⁴ + 1 + 2x² – x² = 0
[ ∵(a + b)² = a²+ b² + lab]
⇒ x⁴ + x² + 1 = 0
⇒ (x²)² + x² + 1 = 0
Let x² = y
∴ y² + y +1 = 0
On comparing with ay² + by + c = 0, we get
a = 1, b = 1 and c = 1
Discriminant, D = b² – 4ac = (1)² – 4(1) (1) = 1 – 4 = -3
Since, D < 0
∴ y² + y + 1 = 0 i.e., x⁴ + x² + 1 = 0 or (x² + 1)² – x² = 0 has no real roots.

Exercise 4.2

Question 1
State whether the following quadratic equations have two distinct real roots. Justify your answer.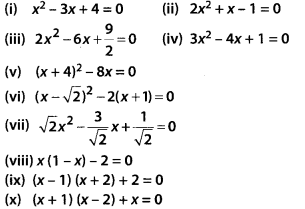

Solution:
(i) Given equation is x² – 3x + 4 = 0
On comparing with ax² + bx + c = 0, we get
a = 1,b = -3 and c = 4
∴ Discriminant, D = b² – 4ac = (-3)² – 4(1)(4)
= 9 – 16 = -7 < 0 i.e., D < 0
Hence, the equation x² – 3x + 4 = 0 has no real roots.

(ii) Given equation is, 2x² + x – 1 = 0
On comparing with ax² + bx + c = 0, we get
a = 2, b = 1 and c = -1
∴ Discriminant, D = b² – 4ac = (1)² – 4(2)(-1)
= 1 + 8 = 9 > 0
i.e., D > 0
Hence, the equation 2x² + x – 1 = 0 has two distinct real roots.

(iii) Given equation is 2x² – 6x + \(\frac { 9 }{ 2 }\) = 0
On comparing with ax² + bx + c = 0, we get
a = 2 ,b = -6 and c = \(\frac { 9 }{ 2 }\)
∴Discriminant, D = b² – 4ac = (-6)² – 4(2) (\(\frac { 9 }{ 2 }\))
= 36 – 36 = 0
i.e., D = 0
Hence, the equation 2x² – 6x + \(\frac { 9 }{ 2 }\) = 0 has equal and real roots.

(iv) Given equation is 3x² – 4x + 1 = 0
On comparing with ax² + bx + c = 0, we get
a = 3,b = -4 and c = 1
∴ Discriminant, D = b² – 4ac
= (-4)² – 4(3)(1)
= 16 – 12 = 4 > 0
i.e., D > 0
Hence, the equation 3x² – 4x + 1 = 0 has
two distinct real roots.

(v) Given equation is (x + 4)² – 8x = 0
⇒ x² + 16 + 8x – 8x = 0
[∵ (a + b)² = a² + b² +2ab]
⇒ x² + 16 = 0
⇒ x² + 0x + 16 = 0
On comparing with ax² + bx + c = 0, we get
a = 1, b = 0 and c = 16
∴ Discriminant, D = b²– 4ac = (0)² – 4(1) (16)
= -64 < 0
i.e., D < 0
Hence the equation (x + 4)² – 8x = 0 has no real roots.

Question 3
A quadratic equation with integral coefficient has integral roots. Justify your answer.
Solution:
No, consider the quadratic equation with integral coefficient
i.e., 2x² + x – 6 = 0.
The root of the quadratic equation are -2 and \(\frac { 3 }{ 2 }\) which are not integers.

Question 4
Does there exist a quadratic equation whose coefficients are rational but both of its roots are irrational? Justify your answer.
Solution:
Yes, consider the quadratic equation with rational coefficient
i.e., 2x² + x – 4 = 0.
The roots of the quadratic equation are \(\frac { -1+\sqrt { 33 } }{ 4\qquad }\) and \(\frac { -1-\sqrt { 33 } }{ 4\qquad }\) which is irrational.

Question 5
Does there exist a quadratic equation whose coefficients are all distinct irrationals but both the roots are rationals? Why?
Solution:
Yes, consider the quadratic equation with all distinct irrationals coefficients
i.e., √3x² – 7√3x + 12√3 = 0.
The roots of this quadratic equation are 3 and 4, which are rationals.

Question 6
Is 0.2 a root of the equation x² – 0.4 = 0? Justify.
Solution:
No, because 0.2 does not satisfy the quadratic equation i.e., (0.2)² – 0.4
= 0.04 – 0.4 = -0.36 ≠ 0

Question 7
If b = 0, c < 0, is it true that the roots of x² + bx + c = 0 are numerically equal and opposite in sign? Justify.
Solution:
Given that b = 0, c < 0 and quadratic equation x² + bx + c = 0 …(i)
Put b = 0 in Eq (i), we get
x² + 0 + c = 0
⇒ x² = -c [Here c < 0 ⇒ -c > 0]
⇒ x = ± √-c
So, the roots of x² + bx + c = 0 are numerically equal and opposite in sign.

Exercise 4.3

Question 1
Find the roots of the quadratic equations by using the quadratic formula in each of the following:
(i) 2x² – 3x – 5 = 0
(ii) 5x² + 13x + 8 = 0
(iii) -3x² + 5x + 12 = 0
(iv) -x² + 7x-10 = 0
(v) x² + 2√2 x – 6 = 0
(vi) x² – 3√5 x + 10 = 0
(vii) \(\frac { 1 }{ 2 }\) x² – √11x + 1 = 0
Solution:
(i) Given equation is 2x² – 3x -5 = 0
On comparing with ax² + bx + c = 0, we get
a = 2, b = -3 and c = -5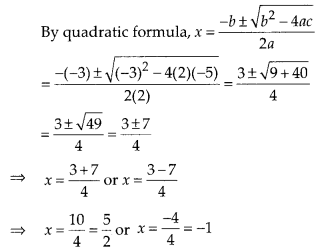

So, the roots of the given equation are \(\frac { 5 }{ 2 }\) and -1.

(ii) Given equation is 5x² + 13x + 8 = 0
On comparing with ax² + bx + c = 0, we get
a = 5, b = 13 and c = 8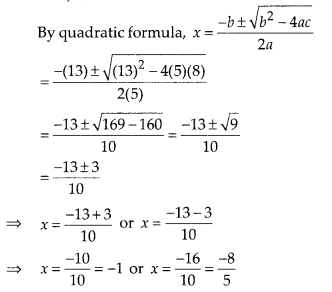

So, the roots of the given equation are -1 and \(\frac { -8 }{ 5 }\) .

(iii) Given equation is -3x² + 5x + 12 = 0
On comparing with ax² + bx + c = 0, we get
a = -3, b = 5 and c = 12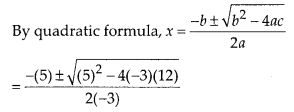


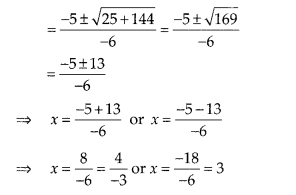
So, the roots of the given equation are \(\frac { -4 }{ 3 }\) and 3.

(iv) Given equation is -x² + 7x – 10 = 0
On comparing with ax² + bx + c = 0, we get
a = -1, b = 7 and c = -10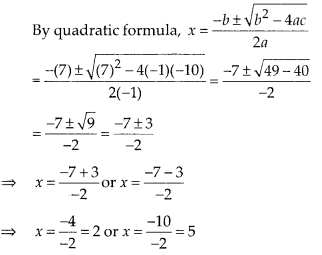

So, the roots of the given equation are 2 and 5.

(v) Given equation is x² + 2√2x – 6 = 0
On comparing with ax²+ bx + c = 0, we get
a = 1 ,b = 2√2 and c = -6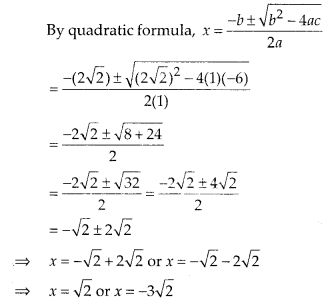

So, the roots of the given equation are √2 and -3√2.

(vi) Given equation is x² – 3√5x + 10 = 0
On comparing with ax² + bx + c = 0, we get
a = 1, b = -3√5 and c = 10
By quadratic formula,

So, the roots of the given equation are 2√5 and √5.

(vii) Given equation is \(\frac { 1 }{ 2 }\) x² – √11x + 1 = 0
On comparing with ax² + bx + c = 0, we get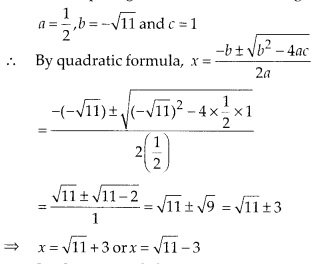

So the roots of the given equation are √11 + 3 and √11 – 3.

Question 2
Find the roots of the following quadratic equations by the factorisation method: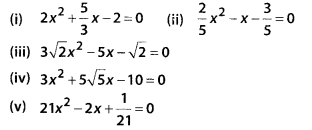

Solution:
Given equation is 2×2 + \(\frac { 5 }{ 3 }\) 2 = 0
On multiplying by 3 on both sides, we get
6x² + 5x – 6 = 0
⇒ 6x² + (9x – 4x) – 6 = 0
[By splitting the middle term]
⇒ 6x² + 9x – 4x – 6 = 0
⇒ 3x(2x + 3) – 2 (2x + 3) = 0
⇒ (2x + 3) (3x – 2) = 0
⇒ 2x + 3 = 0 or 3x – 2 = 0
⇒ x = \(\frac { -3 }{ 2 }\) or x = \(\frac { 2 }{ 3 }\)
Hence, the roots of the equation ,
2x² + \(\frac { 5x }{ 3 }\) – 2 = 0 are \(\frac { -3 }{ 2 }\) and \(\frac { 2 }{ 3 }\).

(ii) Given equation is \(\frac { 2 }{ 5 }\)x² – x – \(\frac { 3 }{ 5 }\) = 0
On multiplying by 5 on both sides, we get
2x² – 5x – 3 = 0
⇒ 2x² – (6x – x) – 3 = 0
[By splitting the middle term]
⇒ 2x² -6x + x- 3 = 0
⇒ 2x(x – 3) + 1(x – 3) = 0
⇒ (x – 3)(2x + 1) = 0
⇒ x – 3 = 0 or 2x + 1= 0
⇒ x = 3 or x = \(\frac { -1 }{ 2 }\)
Hence, the roots of the equation \(\frac { 2 }{ 5 }\) x² – x – \(\frac { 3 }{ 5 }\) = 0 are \(-\frac { 1 }{ 2 }\) and 3.

(iii) Given equation is 3√2x² – 5x – √2 = 0
⇒ 3√2x² – (6x – x) – √2 = 0
[By splitting the middle term]
⇒ 3√2x² – 6x + x – √2 = 0
⇒ 3√2x² – 3√2. √2x + x – √2 = 0
⇒ 3√2x(x – √2) + 1(x – √2) = 0
⇒ (x – √2)(3√2x + 1) = 0
⇒ x – √2 =0 or 3√2x + 1 = 0
⇒ x = √2 or \(x=\frac { -1 }{ 3\sqrt { 2 } } =\frac { -\sqrt { 2 } }{ 6 }\)
Hence, the roots of the equation
3√2x² – 5x – √2 = 0 are \(\frac { -\sqrt { 2 } }{ 6 }\) and √2.

(iv) Given equation is 3x² + 5√5x – 10 = 0
3x² + (6√5 – √5)x – 2√5 x √5 = 0
[By splitting the middle term]
⇒ 3x² + 6√5x – √5x – 2√5 x √5 = 0
⇒ 3x(x + 2√5) – √5(x + 2√5) = 0
⇒ (x + 2√5)(3x – √5) = 0
⇒ x + 2√5 =0 or 3x – √5 = 0
⇒ x = -2√5 or x = \(\frac { \sqrt { 5 } }{ 3 }\)
Hence, the roots of the equation 3x² + 5√5x -10 = 0 are – 2√5 and \(\frac { \sqrt { 5 } }{ 3 }\) .

(v) Given equation is 21x² – 2x + \(\frac { 1 }{ 21 }\) = 0
On multiplying by 21 on both sides, we get
441x² – 42x + 1 = 0
⇒ 441 x² – (21x + 21x) + 1 = 0
[By splitting the middle term]
441x² – 21x – 21x + 1 = 0
⇒ 21x(21x – 1) – 1(21x – 1) = 0
⇒ (21x – 1)(21x – 1) = 0
⇒ 21x – 1 = 0 or 21x -1 = 0
⇒ x = \(\frac { 1 }{ 21 }\) or x = \(\frac { 1 }{ 21 }\)
Hence, the roots of the equation 21x² – 2x + \(\frac { 1 }{ 21 }\) = 0 and \(\frac { 1 }{ 21 }\) and \(\frac { 1 }{ 21 }\).

Exercise 4.4

Question 1
Find whether the following equations have real roots. If real roots exist, find them.
(i) 8x² + 2x – 3 = 0
(ii) -2x² + 3x + 2 = 0
(iii) 5x² – 2x – 10 = 0
(iv) \(\frac { 1 }{ 2x-3 } +\frac { 1 }{ x-5 } =1,\quad x\quad \neq \frac { 3 }{ 2 } ,5\)
(v) x² + 5√5x – 70 = 0
Solution:
(i) Given equation is 8x² + 2x – 3 = 0
On comparing with ax² + bx + c = 0, we get
a = 8, b = 2 and c = -3
∴ Discriminant, D = b² – 4ac
= (2)² – 4(8) (-3) = 4 + 96 = 100 > 0
Therefore, the equation 8x² + 2x – 3 = 0 has two distinct real roots which are given by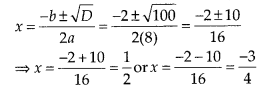

(ii) Given equation is -2x² + 3x + 2 = 0
On comparing with ax² + bx + c- 0, we get
a = -2,b = 3 and c = 2
Discriminant, D = b² – 4ac
= (3)² – 4(-2) (2) = 9 + 16 = 25 > 0
Therefore the equation -2x² + 3x + 2 = 0 has two distinct real roots which are given by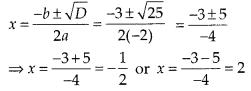

(iii) Given equation is 5x² – 2x – 10 = 0
On comparing with ax² + bx + c = 0 we get a = 5,b = -2 and c = -10
∴ Discriminant, D = b² – 4ac
= (-2)² – 4(5) (-10) = 4 + 200 = 204 > 0
Therefore, the equation 5x² – 2x -10 = 0 has two distinct real roots which are given by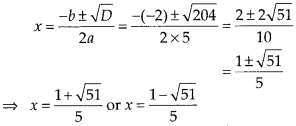

(iv) Given equation is \(\frac { 1 }{ 2x-3 } +\frac { 1 }{ x-5 } =1,\quad x\quad \neq \frac { 3 }{ 2 } ,5\)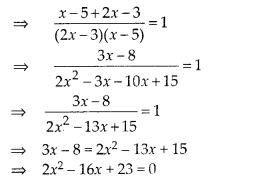

On comparing with ax² + bx + c = 0, we get
a = 2, b = -16 and c = 23
Discriminant, D = b² – 4ac = (-16)² – 4(2) (23)
= 256 – 184
= 72 > 0
Therefore, the equation 2x² – 16x + 23 = 0 has two distinct real roots which are given by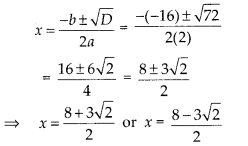

(v) Given equation is x² + 5√5x – 70 = 0 On comparing with ax² + bx + c = 0, we get
a = 1 ,b = 5√5 and c = -70
Discriminant, D = b² – 4ac
= (5√5)² – 4(1)(-70)
= 125 + 280 = 405 > 0
Therefore, the equation x² + 5√5x – 70 = 0 has two distinct real roots which are given by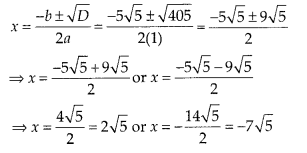

Question 2
Find a natural number whose square diminished by 84 is equal, to thrice of 8 more than the given number.
Solution:
Let n be the required natural number. According to question, n² – 84 = 3(n + 8)
⇒ n² – 84 = 3n + 24
⇒ n² – 3n – 108 = 0
⇒ n² – (12n – 9n) – 108 = 0
[By splitting the middle term]
⇒ n² – 12n + 9n – 108 = 0
⇒ n(n – 12) + 9(n – 12) = 0
⇒ (n – 12)(n + 9) = 0
⇒ n = 12
[n ≠ -9, because 77 is natural number]
Hence, the required natural number is 12.

Question 3
A natural number, when increased by 12, equals 160 times its reciprocal. Find the number.
Solution:
Let the natural number be x.
According to question,
x +12 = \(\frac { 160 }{ x }\)
On multiplying by x on both sides, we get
⇒ x² + 12x – 160 = 0
⇒ x² + (20x – 8x) – 160 = 0
[By splitting the middle term]
⇒ x² + 20x – 8x – 160 = 0
⇒ x(x + 20) – 8(x + 20) = 0
⇒ (x + 20)(x – 8) = 0
⇒ x = 8
[x ≠ – 20, because x is a natural number] Hence, the required natural number is 8.

Question 4
A train, travelling at a uniform speed for 360 km, would have taken 48 minutes less to travel the same distance if its speed were 5 km/h more. Find the original speed of the train.
Solution:
Let the original speed of the train = x km/h
Then, the increased speed of the train = (x + 5)km/h [by given condition]
and distance = 360 km
According to question,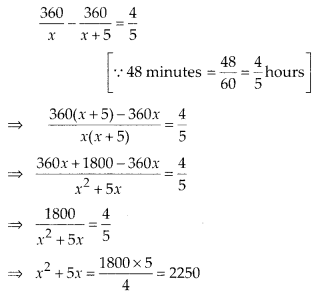

x²+ 5x – 2250 = 0
x²+ (50x – 45x) – 2250 = 0
[By splitting the middle term]
x² + 50x – 45x – 2250 = 0
⇒ x(x + 50) – 45(x + 50) = 0
(x + 50)(x – 45) = 0
⇒ x + 50 = 0 or x – 45 = 0
x ≠ -50 because speed cannot be negative and x – 45 = 0
⇒ x = 45
Hence, the original speed of the train = 45 km/h

Question 5
If Zeba were younger by 5 years than what she really is, then the square of her age (in years) would have been 11 more than five times her actual age. What is her age now?
Solution:
Let the actual age of Zeba = x years
Her age when she was 5 years younger = (x – 5)years
Now, by given condition,
Square of her age = 11 more than five times her actual age
(x – 5)² = 5 x actual age + 11
⇒ (x – 5)² = 5x + 11
⇒ x² + 25 – 10x = 5x + 11
⇒ x² – 15x + 14 = 0
⇒ x² – 14x – x + 14 = 0
[by splitting the middle term]
⇒ x(x – 14) – 1(x – 14) = 0
⇒ (x – 1)(x – 14) = 0
⇒ x = 14 [here, x ≠ 1 because her age is x – 5.
So, x – 5 = 1 – 5 = -4 i.e., age cannot be negative]
Hence, present age of Zeba is 14 years.

Question 6
At present Asha’s age (in years) is 2 more than the square of her daughter Nisha’s age. When Nisha grows to her mother’s present age, Asha’s age would be one year less than 10 times the present age of Nisha. Find the present ages of both Asha and Nisha.
Solution:
Let Nisha’s present age be x years.
Then, Asha’s present age = (x² + 2) years
[by given condition] Now, when Nisha grows to her mother’s present age i.e., after {(x² + 2) – x}yr.
present age i.e., after {(x² + 2) – x}yr. Then,
Asha’s age would be increased by {(x² + 2) – x)yr
Again by given condition
Age of Asha = One year less than 10 times the present age of Nisha
{(x² + 2) + {(x² + 2) – x] = 10x – 1
⇒ 2x² – x + 4 = 10x – 1
⇒ 2x² – 11x + 5 = 0
⇒ 2x² – 10x – x + 5 = 0
⇒ 2x(x – 5) – 1(x – 5) = 0
⇒ (x – 5)(2x – 1) = 0
∴ x = 5
[here, x = \(\frac { 1 }{ 2 }\) cannot be possible because at x = Asha’s age would be 2\(\frac { 1 }{ 4 }\)yrs, which is not possible]
Hence, required age of Nisha = 5 yrs
and required age of Asha = x² + 2 = (5)² + 2 = 25 + 2 =27 yrs.

Question 7
In the centre of a rectangular lawn of dimensions 50 m x 40 m, a rectangular pond has to be constructed so that the area of the grass surrounding the pond would be 1184 m2 [see Figure]. Find the length and breadth of the pond.

Solution:
Given that a rectangular pond has to be constructed in the centre of a rectangular lawn of dimensions 50 m x 40 m so, the distance between pond and lawn would be same around the pond. Say x m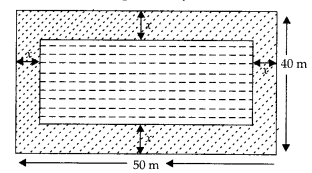

Now, length of rectangular lawn (l₁) = 50 m
and breadth of rectangular lawn (b₁) = 40 m
∴ Length of rectangular pond (l₂)
= 50 – (x + x) = 50 – 2x
and breadth of rectangular pond (b₂)
= 40 – (x + x) = 40 – 2x
Also, area of the grass surrounding the pond =1184 m₂
Area of rectangular lawn – Area of rectangular pond = Area of grass surrounding the pond
l₁ x b₁ – l₂ x b₂ = 1184
[ ∵ area of rectangle = length x bredth]
⇒ 50 x 40 – (50 – 2x) (40 – 2x) = 1184
⇒ 2000 – (2000 – 80x – 100a + 4x₂) = 1184
⇒ 80x + 100x – 4x₂ = 1184
⇒ 4x₂ – 180x +1184 = 0
⇒ x₂ – 45x + 296 = 0
⇒ x₂ – 37x – 8x + 296 = 0
[By splitting the middle term]
⇒ x(x – 37) – 8(x – 37) = 0
⇒ (x – 37) (x – 8) = 0
∴ x = 8
[At x = 37, length and breadth of pond are -24 and -34, respectively but length and breadth cannot be negative. So, x = 37 cannot be possible]
∴ Length of pond = 50 – 2x = 50 – 2(8) = 50 -16 = 34 m
and breadth of pond = 40 – 2x = 40 – 2(8) = 40 -16 = 24 m
Hence, required length and breadth of pond are 34 m and 24 m respectively.

Question 8
At t minutes past 2 pm, the time needed by the minutes hand of a clock to show 3 pm was found to be 3 minutes less than \(\frac { { t }^{ 2 } }{ 4 }\) minutes. Find t.
Solution:
We know that, the time between 2 pm and 3 pm = 1 h = 60 min
Given that, at f minute past 2 pm the time needed by the minute hand of a clock to show 3 pm was found to be 3 min less than
\(\frac { { t }^{ 2 } }{ 4 }\) min i.e,
t + (\(\frac { { t }^{ 2 } }{ 4 }\) – 3 = 60
⇒ 4t + t² – 12 = 240
⇒ t² + 4t – 25² = 0
⇒ t² + 18t – 14t – 252 = 0
[By splitting the middle term]
⇒ t(t + 18) – 14(t+ 18) = 0
⇒ (t + 18)(t – 14) = 0
∴ t = 14 min
[Since, time cannot be negative, so t ≠ 18]
Hence, the required value of t is 14 min.