Chapter 2 Polynomials

NCERT Exemplar Class 10 Maths Chapter 2 Polynomials

Exercise 2.1

Choose the correct answer from the given four options in the following questions :

Question 1
If one of the zeroes of the quadratic polynomial (k – 1)x² + kx + 1 is -3, then the value of k is

Solution:
(A) Let p(x) = (k- 1)x² + kx + 1
Given that, one of the zeroes is -3, then
P(-3) = 0
⇒ (k – 1)(-3)² + k(-3) + 1 = 0
⇒ 9(k – 1) – 3k + 1 = 0
⇒ 6k – 8 = 0
⇒ k = 4/3

Question 2
A quadratic polynomial, whose zeroes are -3 and 4, is
(A) x² – x + 12
(B) x² + x + 12
(C) \(\frac { { x }^{ 2 } }{ 2 } -\frac { x }{ 2 } -6\)
(D) 2x² + 2x – 24
Solution:
(C) Let the zeroes of a quadratic polynomial are α = -3 and β = 4.
Then, sum of zeroes = α + β = -3 + 4 = 1
and product of zeroes = αβ = -3 x 4 = -12
Required polynomial = x² – (sum of zeroes)x + (product of zeroes)
= x² – (1)x + (-12) = x² – x – 12
i.e, \(\frac { { x }^{ 2 } }{ 2 } -\frac { x }{ 2 } -6\)

Question 3
If the zeroes of the quadratic polynomial x² + (o + 1)x + b are 2 and -3, then
(A) a = -7, b = -1
(B) a = 5, b = -1
(C) a = 2, b = -6
(D) a = 0, b = -6
Solution:
(D) Let p(x) = x² + (a + 1)x + b
Given that 2 and -3 are the zeroes of the quadratic polynomial p(x).
∴ p(2) = 0 and p(-3) = 0
p(2) = 0 ⇒ 2² + (a + 1) (2) + b = 0
⇒ 2a + b = -6 … (i)
Now, p(-3) = 0
⇒ (-3)2 + (a + 1)(-3) + b = 0
⇒ 3a – b = 6 ……(ii)
Solving (i) and (ii), we get a = 0,b = -6

Question 4
The number of polynomials having zeroes as -2 and 5 is
(A) 1
(B) 2
(C) 3
(D) more than 3
Solution:
(D) Let p(x) = ax² + bx + c be the required polynomial whose zeroes are -2 and 5.


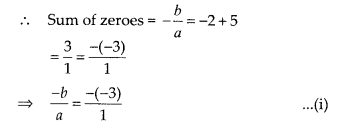
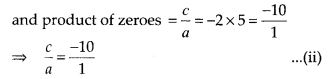
From (i) and (ii), a = 1,b = -3 and c = -10
∴p(x) = x² – 3x – 10
But we know that, if we multiply/divide any polynomial by any arbitrary constant, then the zeroes of polynomial never change.
∴ p(x) = kx² – 3kx – 10k, where, k is a real number
and P(x) = \(\frac { { x }^{ 2 } }{ k } -\frac { 3 }{ k } x-\frac { 10 }{ k }\), where k is a non-zero real number.
Thus, the required number of polynomials is infinite i.e. more than 3.
Hence, out of given options, option (D) is correct.

Question 5
Given that one of the zeroes of the cubic polynomial ax³ + bx² + cx + d is zero, the product of the other two zeroes is

Solution:
(B) Let p(x) = ax³ + bx² + cx + d
Let α ,β, and γ be the zeroes of p(x), where
α = 0.
We know that sum of product of zeroes taken two at a time = \(\frac { c }{ a }\) = αβ + βγ + γα
⇒ 0 x β + βγ + γ x 0 = \(\frac { c }{ a }\)
⇒ βγ = \(\frac { c }{ a }\)
Hence, product of other two zeroes = \(\frac { c }{ a }\)

Question 6
If one of the zeroes of the cubic polynomial x³ + ax² + bx + c is -1, then the product of the other two zeroes is
(A) b – a + 1
(B) b – a – 1
(C) a – b + 1
(D) a – b – 1
Solution:
(A) Let p(x) = x³ + ax² + bx + c
Let α, β and γ be the zeroes of p(x), where α = -1
Now, p(-1) = 0
⇒ (-1)³ + a(-1)² + b(-1) + c = 0
⇒ -1 + a -b + c = 0
⇒ c = 1 – a + b
We know that product of all zeroes

Question 7
The zeroes of the quadratic polynomial x² + 99x + 127 are
(A) both positive
(B) both negative
(C) one positive and one negative
(D) both equal
Solution:
(B) Let p(x) = x² + 99x + 127
Let α and β be the zeroes of p(x).
Then sum of roots = α + β = \(\frac { -b }{ a }\) = -99 … (1)
product of roots = αβ = \(\frac { c }{ a }\) = 127 … (2)
Now, (α – β)² = (α + β)² – 4αβ
= (-99)² – 4 x 127 = 9293
⇒ α – β = \(\sqrt { 9293 }\) = ±96.4
When α – β = 96.4 …(3)
Then solving (1) and (3), we get
α = -1.3, β = -97.7
∴ Both zeroes are negative.
Similarly, for α – β = -96.4, we get both the zeroes are negative.

Question 8
The zeroes of the quadratic polynomial x² + kx + k, k ≠ 0,
(A) cannot both be positive
(B) cannot both be negative
(C) are always unequal
(D) are always equal
Solution:
(A) Let p(x) = x² + kx+ k,k ≠ 0
On comparing p(x) with ax² + bx + c,
we get a = 1,b = k and c = k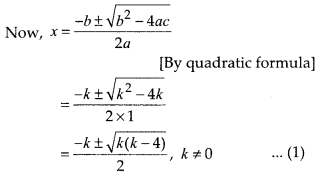


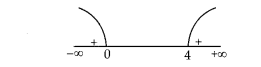
Here, we see that
k(k – 4) > 0
⇒ k ∈ (— ∞, 0) u (4, ∞)

Case I: If k e (- ∞, 0), i.e. k < 0 ⇒ a = 1 >0 ; b, c = k < 0
So, both zeroes are of opposite sign.

Case II: If k E (4, ∞) i.e. k > 4
⇒ a = 1 > 0; b, c = k > 4
So, both zeroes are negative.
Hence, in any case zeroes of the given quadratic polynomial cannot be both positive.

Question 9
If the zeroes of the quadratic polynomial ax² + bx + c, c ≠ 0 are equal, then
(A) c and a have opposite signs
(B) c and b have opposite signs
(C) c and a have the same sign
(D) c and b have the same sign
Solution:
(C) The zeroes of the given quadratic polynomial ax² + bx + c where c ≠ 0, are equal, if coefficient of x² and constant term have the same sign i.e.
c and a have the same sign.
While b i.e., coefficient of x can be positive or negative but not zero.
Consider, (i) x² + 4x + 4 = 0
⇒ (x +2)² = 0
⇒ x = -2, -2 and

(ii) x² – 4x + 4 = 0
⇒ (x – 2)² = 0
⇒ x = 2, 2

Question 10
If one of the zeroes of a quadratic polynomial of the form x²+ ax + b is the negative of the other, then it
(A) has no linear term and the constant term is negative.
(B) has no linear term and the constant term is positive.
(C) can have a linear term but the constant term is negative.
(D) can have a linear term but the constant term is positive.
Solution:
(A) Let p(x) = x² + ax + b and by given condition the zeroes are a and -a
∴ Sum of the zeroes = α – α = 0
⇒ α = 0
⇒ p(x) = x² + b, which cannot be linear and product of zeroes = α(-α) = b
⇒ -α² = b
which is only possible when b < 0.
Hence, it has no linear term and the constant term is negative.

Question 11
Which of the following is not the graph of a quadratic polynomial?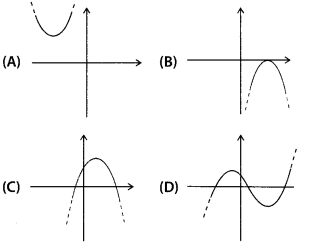

Solution:
(D) For any quadratic polynomial ax² + bx + c, a ≠ 0, the graph of the corresponding equation y = ax² + bx + c has one of the two shapes either open upwards like or open downwards like depending on whether a > 0 or a < 0. These curves are called parabolas.
So, option (D) cannot be possible.
Also, the curve of a quadratic polynomial crosses the X-axis at most two point but in option (D), the curve crosses the X-axis at the three points, so it does not represent the quadratic polynomial.

Exercise 2.2

Question 1
Answer the following and justify:
(i) Can x² – 1 be the quotient on division of x⁶ + 2x³ + x – 1 by a polynomial in x of degree 5?
(ii) What will the quotient and remainder be on division of ax²+ bx + c by px³ + qx² + rx + s, p ≠ 0?
(iii) If on division of a polynomial p(x) by a polynomial g(x), the quotient is zero, what is the relation between the degrees of p(x) and g(x)?
(iv) If on division of a non-zero polynomial p(x) by a polynomial g(x), the remainder is zero, what is the relation between the degrees of p(x) and g(x)?
(v) Can the quadratic polynomial x² + kx + k have equal zeroes for some odd integer k > 1?
Solution:
(i) Let divisor be a polynomial in x of degree 5 = ax⁵ + bx⁴ + cx³ + dx² + ex + f
Quotient = x² – 1
and dividend = x⁶ + 2x³ + x – 1
By division algorithm, we have
dividend = divisor x quotient + remainder
= (ax⁵ + bx⁴ + cx³ + dx² + ex +f) x (x² – 1) + remainder
= (a polynomial of degree 7)
But dividend is a polynomial of degree 6.
So, division algorithm is not satisfied.
Hence, x² – 1 can’t be the quotient.

(ii) Given that, divisor
= px³ + qx² + rx + s, p ≠ 0
and dividend = ax² + fox + c We see that
degree of divisor > degree of dividend
So, by division algorithm,
quotient = 0 and remainder = ax² + bx + c

(iii) If division of a polynomial p(x) by a polynomial g(x), the quotient is zero, degree of p(x) < degree of g(x).

(iv) If division of a non-zero polynomial p(x) by a polynomial g(x), the remainder is zero, then g(x) is a factor of p(x) and has degree less than or equal to the degree of p(x).

(v) Let p(x) = x² + kx + k
If p(x) has equal zeroes, then its discriminant should be zero.
∴ d = b² – 4ac = 0 … (i)
On comparing p(x) with ax² + bx + c, we get
a = 1,b = k and c = k
∴ (k²) – 4(1)(k) = 0
⇒ k(k – 4) = 0
⇒ k = 0, 4
So, the quadratic polynomial p(x) have equal zeroes only at k = 0, 4.
So the given statement is not correct.

Question 2
Are the following statements ‘True’ or ‘False’? Justify your answers.
(i) If the zeroes of a quadratic polynomial ax² + bx + c are both positive, then a, b and c all have the same sign.
(ii) If the graph of a polynomial intersects the x-axis at only one point, it cannot be a quadratic polynomial.
(iii) If the graph of a polynomial intersects the x-axis at exactly two points, it need not be a quadratic polynomial.
(iv) If two of the zeroes of a cubic polynomial are zero, then it does not have linear and constant terms.
(v) If all the zeroes of a cubic polynomial are negative, then all the coefficients and the constant term of the polynomial have the same sign.
(vi) If all three zeroes of a cubic polynomial x³ + ax² – bx + c are positive, then at least one of a, b and c is non-negative.
(vii) The only value of k for which the quadratic polynomial kx² + x + k has equal zeroes is 1/2.
Solution:
(i) False
If the zeroes of a quadratic polynomial ax² + bx + c are both positive, then
α + β = \(-\frac { b }{ a }\) and αβ = \(\frac { c }{ a }\)
where α and β are the zeroes of the quadratic polynomial and α, β > 0.
∴ c < 0, a < 0 and b > 0
or c > 0, a > 0 and b < 0

(ii) False
If the graph of a polynomial intersects the x-axis at only one point, then it cannot be a quadratic polynomial because a quadratic polynomial may touch the x-axis at exactly one point or intersects x-axis at exactly two points or do not touch the x-axis.

(iii) True
If the graph of a polynomial intersects the x-axis at exactly two points, then it may or may not be a quadratic polynomial. As, a polynomial of degree more than 2 is possible which intersects the x-axis at exactly two points when it has two real roots and other imaginary roots.

(iv) True
Let α, β and γ be the zeroes of a cubic polynomial and given that two of the given zeroes have value 0.
Let β = γ = 0 and
p(x) = (x – α)(x – β)(x – γ)
= (x – α)(x – 0)(x – 0)
= x³ – αx²
which does not have linear and constant terms.

(v) True
If p(x) = ax³ + bx² + cx + d
Then for all negative roots, a, b, c and d must have same sign.

(vi) False
Let α, β and γ be the three zeroes of cubic polynomial x³ + ax² – bx + c.
Then, product of zeroes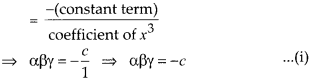

Given that, all three zeroes are positive.
So, the product of all three zeroes is also positive.
i.e., αβγ > 0
⇒ -c > 0 [from (i)]
⇒ c <0
Now, sum of the zeroes = α + β + γ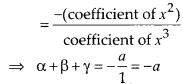

But α, β and γ all are positive. Thus, their sum is also positive. So, α + β + γ > 0 ⇒ -a > 0 ⇒ a < 0
and sum of the product of the zeroes taken two at a time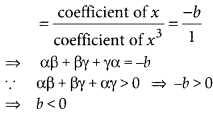

∴ All the coefficients a, b and c are negative,

(vii) False
It is given that the quadratic polynomial kx² + x + k has equal zeroes.
∴ b² – 4ac = 0 i.e., discriminant is zero
⇒ (1)² – 4(k)(k) = 0
⇒ 1 – 4k² = 0
⇒ 4k² = 1
⇒ k = \(\frac { 1 }{ 4 }\)
⇒ k = ± \(\frac { 1 }{ 2 }\)
So, for two values of k, given quadratic polynomial has equal zeroes.

Exercise 2.3

Find the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials:

Question 1
4x² – 3x – 1
Solution:
Let p(x) = 4x² – 3x – 1
= 4x² – 4x + x – 1
= 4x (x – 1) + 1(x – 1)
= (x – 1)(4x + 1)
So, the zeroes of p(x) are 1 and -1/4.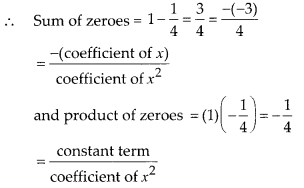

Question 2
3x² + 4x – 4
Solution:
Let p(x) = 3x² + 4x -4
= 3x² + 6x – 2x – 4
= 3x (x + 2) – 2(x + 2)
= (x + 2)(3x – 2)
So, the zeroes of p(x) are -2 and 2/3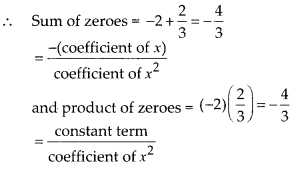

Question 3
5t² + 12t+ 7
Solution:
Let p(t) = 5t² + 12t + 7
= 5t² + 7t + 5t + 7
= (5t + 7)(t + l)
So, the zeroes of p(t) are -7/5 and -1

Question 4
t³ – 2t – 15t
Solution:
Let p(t) = t³ – 2t² – 15t
=t(t² – 2t – 15)
= t(t² – 5t + 3t – 15)
= t(t – 5)(t + 3)
So the zeroes of p(t) are -3, 0 and 5.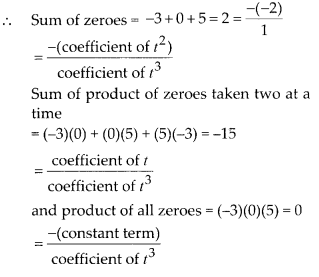

Question 5
\( 2{ x }^{ 2 }+\frac { 7 }{ 2 } x+\frac { 3 }{ 4 }\)
Solution:
Let p(x) = 2x² + \(\frac { 7 }{ 2 }\) x + \(\frac { 3 }{ 4 }\) = 8x² + 14x+3
= 8x² + 12x + 2x + 3
= (2x + 3)(4x + 1)
So, the zeroes of p(x) are \(-\frac { 3 }{ 2 }\) and \(-\frac { 1 }{ 4 }\)

Question 6
4x² + 5√2x – 3
Solution:
Let p(x) = 4x² + 5√2x – 3
= 4x² + 6√2x – √2x – 3
= 2√2x(√2x+3) – 1(√2x + 3)
= (√2x + 3)(2√2x – 1)

Question 7
2s² – (1 + 2√2)s + √2
Solution:
Let p(s) = 2s² – (1 + 2√2)s + √2
= 2s² – s – 2√2s + √2
= 2s – 1 (s – √2)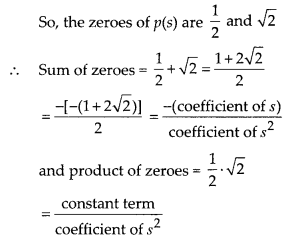

Question 8
v² + 4√3v – 15
Solution:
Let p(v) = v² + 4√3v – 15
= v² + 5√3v – √3v – 15
= (v + 5√3) (v -√3)
So, the zeroes of p(ν) are 5√3 and √3
∴ Sum of zeroes = -5√3 + √3 = -4√3

Question 9
y² + \(\frac { 3 }{ 2 }\)√5y – 5
Solution:
Let p(y) = y² + \(\frac { 3 }{ 2 }\)√5y – 5
= 2y² + 3√5y – 10
= 2y² + 4√5y – √5y – 10
= (y + 2√5)(2y – √5)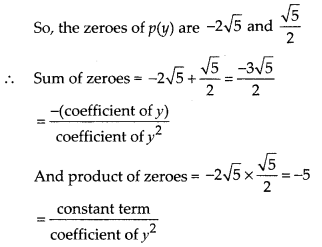

Question 10
7y² – \(\frac { 11 }{ 3 }\)y – \(\frac { 2 }{ 3 }\)
Solution:
Let p(y) = 7y² – \(\frac { 11 }{ 3 }\)y – \(\frac { 2 }{ 3 }\)
= 21y² – 11y – 2
= 21y² – 14y + 3y – 2
= (3y – 2) (7y + 2)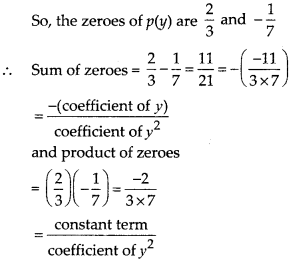

Exercise 2.4

Question 1
For each of the following, find a quadratic polynomial whose sum and product respectively of the zeroes are as given. Also find the zeroes of these polynomials by factorisation.

Solution:
(i) Given that, sum of zeroes (S) = \(-\frac { 8 }{ 3 }\)
and product of zeroes (P) = \(\frac { 4 }{ 3 }\)
∴ Required quadratic polynomial is p(x) = x² – sx + P
= x² + \(-\frac { 8 }{ 3 }\)x + \(-\frac { 4 }{ 3 }\)
i.e., 3x² + 8x + 4
Using factorisation method,
p(x) = 3x² + 6x + 2x + 4 = (x + 2)(3x + 2)
Hence, the zeroes of p(x) are -2 and \(-\frac { 2 }{ 3 }\)

(ii) Given that, sum of zeroes (S) = \(-\frac { 21 }{ 8 }\) and
Product of zeroes (P) = \(-\frac { 5 }{ 16 }\)
∴ Required quadratic polynomial is p(x) = x² – Sx + P
= x² – \(-\frac { 21 }{ 8 }\) x + \(-\frac { 5 }{ 16 }\)
i.e., 16x² – 42x + 5
Using factorisation method,
p(x) = 16x² – 40x – 2x + 5 = (2x – 5)(8x – 1)
Hence, the zeroes of p(x) are \(-\frac { 5 }{ 2 }\) arid \(-\frac { 1 }{ 8 }\).

(iii) Given that, sum of zeroes (S) = -2√3 and
product of zeroes (P) = – 9
Required quadratic polynomial is p(x) = x² – Sx + P = x2 + 2√3x – 9
Using factorisation method, p(x) = x² + 3√3x – √3x – 9
= (x + 3√3)(x – √3)
Hence, the zeroes of p(x) are -3√3 and √3

(iv) Given that, sum of zeroes (S) = \(-\frac { 3 }{ 2\sqrt { 5 } }\)
Product of zeroes (P) = \(-\frac { 1 }{ 2 }\)
∴ Required quadratic polynomial is
p(x) = x² – Sx + P = x² + \(-\frac { 3 }{ 2\sqrt { 5 } }\)x – \(-\frac { 1 }{ 2 }\)
i.e., 2√5 x² + 3x – √5
Using factorisation method,
p(x) = 2√5x² + 5x – 2x – √5
= (2x + √5) (√5 – 1)
Hence, the zeroes of p(x) are \(-\frac { \sqrt { 5 } }{ 2 }\) and \(\frac { 1 }{ \sqrt { 5 } }\)

Question 2
Given that the zeroes of the cubic polynomial x³ – 6x² + 3x +10 are of the form a,a + b,a + 2b for some real numbers a and b, find the values of a and b as well as the zeroes of the given polynomial.
Solution:
Let p(x) = x³ – 6x² + 3x + 10
Given that a, (a + b) and (a + 2b) are the zeroes of p(x). Then,

⇒ a(a + b) + (a + b)(a + 2b) + a(a + 2b) = \(\frac { 3 }{ 1 }\)
⇒ 2a + 2(2 + b) + a(2 + b) = 3 [Using (i)]
⇒ 2a + 2(2 + 2 – a) + a(2 + 2 – a) – 3
⇒ 2a + 8 – 2a + 4a – a² = 3
⇒ -a² + 4a + 5 = 0
⇒ a² – 4a – 5 = 0
Using factorisation method,
a² – 5a + a – 5 = 0
⇒ (a – 5)(a + 1) = 0
⇒ a = -1, 5
When a = -1, then b = 3
When a = 5, then b = -3
Hence for a = -l, b = 3 zeroes of p(x) are
a, (a + b), (a + 2b) i.e„ -1, (-1 + 3), (-1 + 6) or -1, 2, 5
When a = 5 and b = -3, then zeroes of p(x) are a, (a + b), (a + 2b)
i.e, 5, (5 – 3), (5 – 6) or 5, 2, -1
So, the required values are a = -1, b = 3 or a = 5, b = -3 and the zeroes of p(x) are -1, 2 and 5.

Question 3
Given that √2 is a zero of the cubic polynomial 6x³ + √2x² -10x – 4√2, find its other two zeroes.
Solution:
Let p(x) = 6x³ + √2x² -10x – 4√2
Since (x – √2) is one of the factors of given cubic polynomial.
∴ By using division algorithm,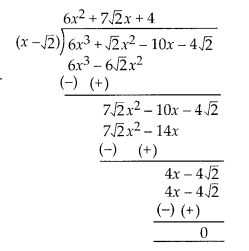

∴ p(x) = 6x³ + √2x² -10x – 4√2
= (6x² + 7√2x + 4)(x – √2) + 0
= (x – √2)(6x² + 4√2x + 3√2x + 4)
= (x – √2)(√2x + 1)(3√2x + 4)
So, other zeroes of p(x) are \(-\frac { 1 }{ \sqrt { 2 } }\) and \(-\frac { 4 }{ 3\sqrt { 2 } }\) .

Question 4
Find k so that x² + 2x + k is a factor of 2x⁴ + x³ – 14x² + 5x + 6. Also find all the zeroes of the two polynomials.
Solution:
Using division algorithm, we get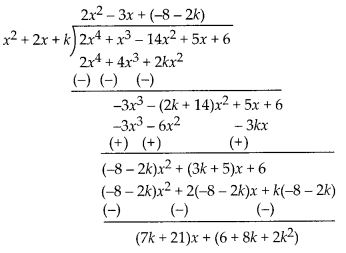

Since, (x² + 2x + k) is a factor of
2x⁴ + x³ – 14x² + 5x + 6
So, remainder should be zero.
⇒ (7k + 21 )x + (2k² + 8k + 6) = 0-x + 0
⇒ 7k + 21 = 0 and 2k² + 8k + 6 = 0
⇒ k = -3 or k² + 4k + 3 = 0
⇒ k² + 3k + k + 3 = 0
⇒ (k + 1)(k + 3) = 0
⇒ k = -1 or -3
For k = -3, remainder is zero.
∴ The required value of k = -3.
Also, dividend = divisor x quotient + remainder
⇒ 2x⁴ + x³ – 14x² + 5x + 6 = (x² + 2x – 3)(2x² – 3x – 2)
= (x² + 3x – x – 3)(2x² – 4x + x – 2)
= (x – 1)(x + 3)(x – 2)(2x + 1)
Hence, the zeroes of x² + 2x – 3 are 1, -3 and the zeroes of 2x² – 3x – 2 are 2,\(-\frac { 1 }{ 2 }\) .
Thus, the zeroes of 2x⁴ + x³ – 14x² + 5x + 6 are 1, -3, 2, \(-\frac { 1 }{ 2 }\).

Question 5
Given that x – √5 is a factor of the cubic polynomial x³ – 3√5x² +13x – 3√5, find all the zeroes of the polynomial.
Solution:
Let p(x) = x³ – 3√5x² +13x – 3√5
Using division algorithm,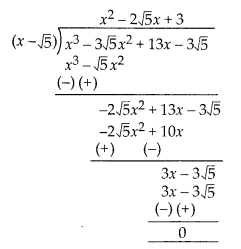

∴ x³ – 3√5x² + 13x – 3√5
= (x² – 2√5x + 3)(x – √5 )
= (x – √5 )[x² – {(√5 + √2 ) + (√5 – √2 )x + 3]
= (x – √5)[x² – (√5 + √2)x – (√5 – √2)x + (√5 + √2)(√5 – √2)]
= (x – √5){x-(√5 + √2)){x- (√5 – √2)}
So, all the zeroes of the given polynomial are
√5, (√5 + √2) and ( √5 – √2).

Question 6
For which values of a and b, are the zeroes of q(x) = x² + 2x² + a are also the zeroes of the polynomial p(x) = x⁵ – x⁴ – 4x³ + 3x² + 3x + b? Which zeroes of p(x) are not the zeroes of p(x)?
Solution:
Since zeroes of q(x) = x² + 2x² + a are also the zeroes of the polynomial
p(x) = x⁵ – x⁴ – 4x³ + 3x² + 3x + b
So, q(x) is a factor of p(x). Then, we use a division algorithm.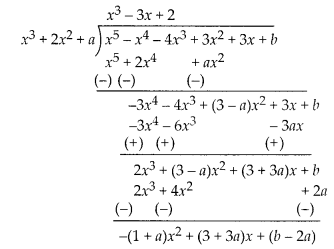

⇒ -(1 + a)x² + (3 + 3a)x + (b – 2a) = 0
= 0.x² + 0.x + 0
On comparing the coefficient of x² and constant term, we get
a + 1 = 0 ⇒ a = – 1
and b – 2a = 0 ⇒ b = 2a
⇒ b = 2(-1) = -2
For a = -1 and b = -2, the zeroes of q(x) are also the zeroes of the polynomial p(x). q(x) = x³ + 2x² – 1
and p(x) = x⁵ – x⁴ – 4x³ + 3x² + 3x – 2
Since, dividend = divisor x quotient + remainder
p(x) = (x³ + 2x² – 1)(x² – 3x + 2) + 0
= (x³ + 2x² – 1)(x – 2)(x – 1)
So, the zeroes of p(x) are 1 and 2 which are not the zeroes of q(x).