Chapter 13 Statistics and Probability

NCERT Exemplar Problems Class 10 Maths Solutions Chapter 13 Statistics and Probability

Exercise 13.1 Multiple Choice Questions (MCQs)

Question 1:

(a) lower limits of the classes                           (b) upper limits of the classes
(c) mid-points of the classes                             (d) frequencies of the class marks
Solution:
(c) We know that, \({d}_{i}\) = \({ x }_{ i }\) – a
i.e., \({d}_{i}\)‘s are the deviation from a of mid-points of the classes.

Question 2:
While computing mean of grouped data, we assume that the frequencies are
(a) evenly distributed over all the classes
(b) centred at the class marks of the classes
(c) centred at the upper limits of the classes
(d) centred at the lower limits of the classes
Solution:
(b) In computing the mean of grouped data, the frequencies are centred at the class marks of the classes.

Question 3:


(a) 0                  (b) -1                           (c) 1                         (d) 2
Solution: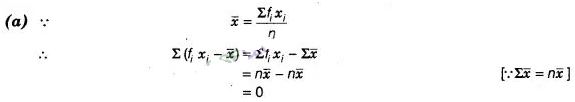

Question 4: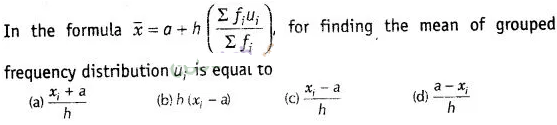

Solution: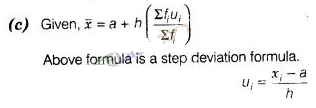

Question 5:
The abscissa of the point of intersection of the less than type and of the more than type cumulative frequency curves of a grouped data gives its
(a) mean                     (b) median                               (c) mode                                 (d) All of these
Solution:
(b) Since, the intersection point of less than ogive and more than ogive gives the median on the abscissa.

Question 6:
For the following distribution,

the sum of lower limits of the median class and modal class is
(a) 15                                (b) 25                                    (c) 30                         (d) 35
Solution: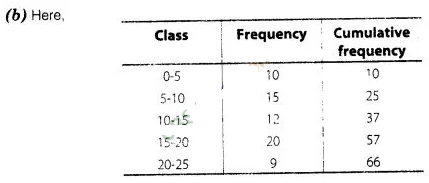

Now,\(\frac{N}{2} =\frac{66}{2}\)= 33, which lies in the interval 10-15. Therefore, lower limit of the median class is 10.                                              .         ,
The highest frequency is 20, which lies in the interval 15-20. Therefore, lower limit of modal class is 15. Hence, required sum is 10 + 15 = 25.

Question 7:
Consider the following frequency distribution

The upper limit of the median class is
(a) 7                                (b) 17.5                      (c) 18                                 (d) 18.5
Solution: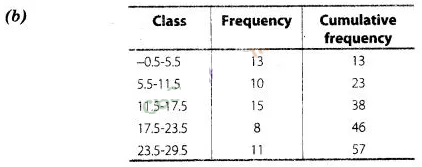

Question 8:
For the following distribution,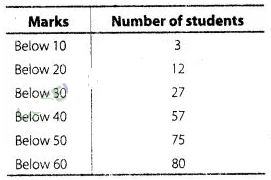

the modal class is
(a) 10-20                             (b) 20-30            (c) 30-40                           (d) 30-40
Solution:

Here,we see that  the highest frequency is 30. which lies in the interval 30-40.

Question 9:
consider the data.

The difference of the upper limit of the median class and the lower limit of the modal class is
(a) 0                                (b) 19                                  (c) 20                                (d) 38
Solution: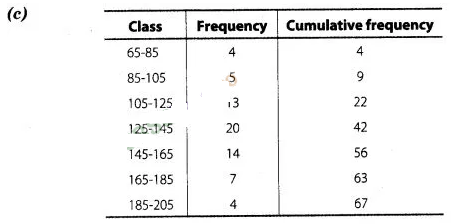

Here,\(\frac{N}{2} =\frac{67}{2}\) = 33.5 which lies in the interval 125 -145.
Hence, upper limit of median class is 145.
Here, we see that the highest frequency is 20 which lies in 125-145. Hence, the lower limit of modal class is 125.
Required difference = Upper limit of median class – Lower limit of modal class
= 145-125 = 20

Question 10:
The times (in seconds) taken by 150 atheletes to run a 110 m hurdle race are tabulated below

The number of atheletes who completed the race in less than 14.6 s is
(a) 11                        (b) 71                        (c) 82                         (d) 130
Solution:
(c) The number of atheletes who completed the race in less than 14.6
= 2 + 4+ 5+71 =82

Question 11:
Consider the following distribution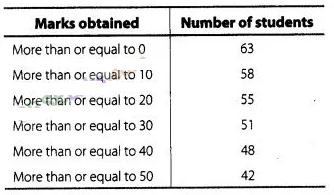

the frequency of the class 30-40 is
(a) 3                          (b) 4                                 (c) 3                          (d) 4
Solution: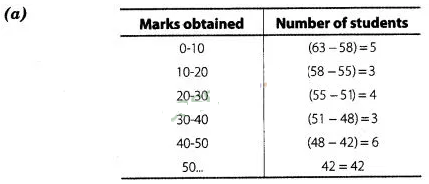

Hence,frequency in the class interval 30-40 is 3

Question 12:
If an event cannot occur, then its probability is
(a) 1                          (b) \(\frac{3}{4}\)                          (c) \(\frac{1}{2}\)                 (d) 0
Solution:
(d) The event which cannot occur is said to be impossible event and probability of impossible event is zero.

Question 13:
Which of the following cannot be the probability of an event?
(a) \(\frac{1}{2}\)                    (b) 0.1                   (c) 3                        (d) \(\frac{17}{16}\)
Solution:
(d) Since, probability of an event always lies between 0 and 1.

Question 14:
An event is very unlikely to happen. Its probability is closest to
(a) 0.0001                   (b) 0.001                               (c) 0.01                                    (d) 0.1
Solution:
(a) The probability of an event which is very unlikely to happen is closest to zero and from the given options 0.0001 is closest to zero.

Question 15:
If the probability of an event is P, then the probability of its completmentry event will be
(a) P -1                     (b)    P                      (c)    1 – P                   (d) 1 — \(\frac{1}{P}\)
Solution:
(c) Since, probability of an event + probability of its complementry event = 1
So, probability of its complementry event = 1 – Probability of an event = 1 – P

Question 16:
The probability expressed as a percentage of a particular occurrence can never be
(a) less than 100                                        (b) less than 0
(c) greater than 1                                       (d) anything but a whole number
Solution:
(b) We know that, the probability expressed as a percentage always lie between 0 and 100. So, it cannot be less than 0.

Question 17:
If P (A) denotes the probability of an event A, then
(a) P(A) < 0                          (b) P(A) > 1                        (c)  0 ≤ P(A) ≤ 1                        (d)  -1 ≤ P(A) ≤ 1
Solution:
(c) Since, probability of an event always lies between 0 and 1.

Question 18:
If a card is selected from a deck of 52 cards, then the probability of its being a red face card is
(a) \(\frac{3}{26}\)                        (b) \(\frac{3}{13}\)                                  (c)  \(\frac{2}{13}\)                                    (d)  \(\frac{1}{2}\)
Solution:
(c) In a deck of 52 cards, there are 12 face cards i.e.,6 red and 6 black cards.
So, probability of getting a red face  card = \(\frac{6}{52} =\frac{3}{26}\)

Question 19:
The probability that a non-leap your selected at random will contains 53 Sunday is           ‘
(a) \(\frac{1}{7}\)                        (b) \(\frac{2}{7}\)                                  (c)  \(\frac{3}{7}\)                                    (d)  \(\frac{5}{7}\)
Solution:
(a) A non-leap year has 365 days and therefore 52 weeks and 1 day. This 1 day may be Sunday or Monday or Tuesday or Wednesday or Thursday or Friday or Saturday. Thus, out of 7 possibilities, 1 favourable event is the event that the one day is Sunday.
∴ Required probability = \(\frac{1}{7}\)

Question 20:
When a die is thrown, the probability of getting an odd number less than 3 is ,
(a) \(\frac{1}{6}\)                        (b) \(\frac{1}{3}\)                                  (c)  \(\frac{1}{2}\)                                    (d)  0
Solution:
(a) When a die-is thrown,then total number of outcomes = 6 Odd number less than 3 is 1 only.
Number of possible outcomes = 1
Required probability = \(\frac{1}{6}\)

Question 21:
A card is drawn from a deck of 52 cards. The event E is that card is not an ace of hearts. The number of outcomes favourable to E is
(a) 4                           (b) 13                        (c) 48                       (d) 51
Solution:
(d) In a deck of 52 cards, there are 13 cards of heart and 1 is ace of heart.
Hence, the number of outcomes favourable to E = 51

Question 22:
The probability of getting a bad egg in a lot of 400 is 0.035. The number of bad eggs in the lot is
(a) 7                           (b) 14                        (c) 21                       (d) 28
Solution:
(b) Here,                           total number of eggs = 400
Probability of getting a bad egg = 0.035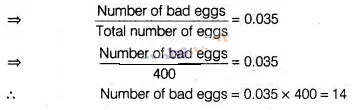

Question 23:
A girl calculates that the probability of her winning the first prize in a lottery is 0.08. If 6000 tickets are sold, then how many tickets has she bought?
(a) 40                        (b) 240                       (c) 480                      (d) 750
Solution:
(c) Given, total number of sold tickets = 6000
Let she bought x tickets.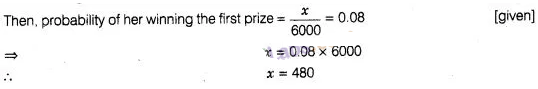

Hence, she bought 480 tickets.

Question 24:
One ticket is drawn at random from a bag containing tickets numbered 1 to 40. The probability that the selected ticket has a number which is a multiple of 5 is
(a) \(\frac{1}{5}\)                        (b) \(\frac{3}{5}\)                                  (c)  \(\frac{4}{5}\)                                    (d)  \(\frac{1}{3}\)
Solution:
(a) Number of total outcomes = 40
Multiples of 5 between 1 to 40 = 5,10,15,20,25. 30 35, 40

Question 25:
Someone is asked to take a number from 1 to 100. The probability that it is a prime,is
(a) \(\frac{1}{5}\)                        (b) \(\frac{6}{25}\)                                  (c)  \(\frac{1}{4}\)                                    (d)  \(\frac{13}{50}\)
Solution:
(c) Total numbers of outcomes = 100
So, the prime numbers between 1 to 100 are 2, 3, 5, 7,11,13,17,19, 23, 29, 31,37, 41. 43, 47, 53, 56, 61, 67, 71, 73, 79, 83, 89 and 97.

Question 26:
A school has five houses A, B, C, D and E. A class has 23 students, 4 from house A, 8 from house B, 5 from house C, 2 from house D and rest from house E. A single student is selected at random to be the class monitor. The probability that the selected student is not from A, B and C is
(a) \(\frac{4}{23}\)                        (b) \(\frac{6}{23}\)                                  (c)  \(\frac{8}{23}\)                                (d)  \(\frac{17}{23}\)
Solution:
(b) Total number of students = 23
Number of students in house A, B and C = 4+ 8 + 5 = 17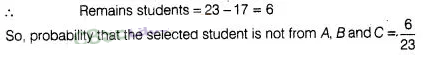

Exercise 13.2 Very Short Answer Type Questions

Question 1:
The median of an ungrouped data and the median calculated when the same data is grouped are always the same. Do you think that this is a correct statement? Give reason.
Solution:
Not always, because for calculating median of a grouped data, the formula used is based on the assumption that the observations in the classes are uniformal distributed (or equally spaced).

Question 2:
In calculating the mean of grouped data, grouped in classes of equal width, we may use the formula,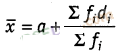

Where, a is the assumed mean, a must be one of the mid-point of the classes. Is the last statement correct? Justify your answer.
Solution:
No, it is not necessary that assumed mean consider as the mid-point of the class interval. It is considered as any value which is easy to simplify it.

Question 3:
Is it true to say that the mean, mode and median of grouped data will always be different? Justify your answer
Solution:
the value of these three measures can be the same, it depends on the type of data.

Question 4:
Will the median class and modal class of grouped data always be different? Justify your answer.
Solution:
Not always, It depends on the given data.

Question 5:
In a family having three children, there may be no girl, one girl, two girls or three girls. So, the probability of each is \(\frac{1}{4}\) . Is this correct? Justify your answer.
Solution:
No, the probability of each is not \(\frac{1}{4}\) because the probability of no girl in three children is zero and probability of three girls in three children is one.
Justification
So, these events are not equally likely as outcome one girl, means gbb, bgb, bbg ‘three girls’ means ‘ggg’ and so on.

Question 6:
A game consists of spinning an arrow which comes to rest pointing at one of the regions (1, 2 or 3) (see figure). Are the outcomes 1, 2 and 3 equally likely to occur? Give reasons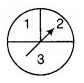

Solution:
No, the outcomes are not equally likely, because 3 contains half part of the
total region, so it is more likely than 1 and 2, since 1 and 2, each contains half part of the remaining part of the region.

Question 7:
Apoorv throws two dice once and computes the product of the numbers appearing on the dice. Peehu throws one die and squares the number that appears on it. Who has the better chance of getting the number 36? Why?
Solution:
Apoorv throws two dice once.
So total number of outcomes = 36
Number of outcomes for getting product 36 = 1 (6 x 6)

Hence, Peehu has better chance of getting the number 36.

Question 8:
When we toss a coin, there are two possible outcomes-head or tail. Therefore, the probability of each outcome is \(\frac{1}{2}\). Justify your answer
Solution:
Yes, probability of each outcome is \(\frac{1}{2}\) because head and tail both are equally likely events.

Question 9:
A student says that, if you throw a die, it will show up 1 or not 1. Therefore, the probability of getting 1 and the probability of getting not 1. each is equal to \(\frac{1}{2}\). Is this correct? Give reasons.
Solution:
No, this is not correct.
Suppose we throw a die, then total number of outcomes = 6
Possible outcomes = 1 or 2 or 3 or 4 or 5 or 6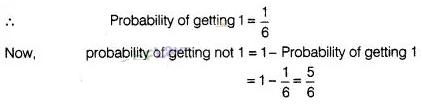

Question 10:
I toss three coins together. The possible outcomes are no heads, 1 head,2 head and 3 heads. So, I say that probability of no heads is \(\frac{1}{4}\). What is wrong with this conclusion?
Solution:
I toss three coins together                                                                                                      [given]
So, total number of outcomes = 2³ = 8
and possible outcomes are (HHH), (HTT), (THT), (TTH),(HHT), (THH), (HIH)and (TTT)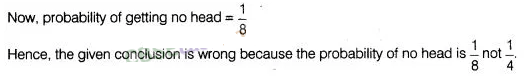

Question 11:
If you toss a coin 6 times and it comes down heads on each occasion. Can you say that the probability of getting a head is 1? Given reasons.
Solution:
No. if let we toss a coin, then we get head or tail, both are equally likely events So,probability is \(\frac{1}{2}\). If we toss a coin 6 times, then probability will be same in each case. So, the 2
probability of getting a head is not 1.

Question 12:
Sushma tosses a coin 3 times and gets tail each time. Do you think that the outcome of next toss will be a tail? Give reasons.
Solution:
The outcome of next toss may or may not be tail, because on tossing a coin, we get head or tail so both are equally likely events.

Question 13:
If I toss a coin 3 times and get head each time, should I expect a tail to have a higher chance in the 4th toss? Give reason in support of your answer.
Solution:
No, let we toss a coin, then we get head or tail, both are equaly likely events i.e., probability of each event is \(\frac{1}{2}\). So, no question of expecting a tail to have a higher chance in 4th toss.

Question 14:
A bag contains slips numbered from 1 to 100. If Fatima chooses a slip at random from the bag, it will either be an odd number or an even number. Since, this situation has only two possible outcomes, so the 1
probability of each is \(\frac{1}{2}\). Justify.
Solution:
We know that, between 1 to 100 half numbers are even and half numbers are odd i.e., 50 numbers (2, 4, 6, 8…. 96, 98,100) are even and 50 numbers (1,3, 5, 7. . , 97, 99) are odd.
So, both events are equally likely.

Exercise 13.3 Short Answer Type  Questions

Question 1:
Find the mean of the distribution

Solution:
We first, find the class mark x_i, of each class and then proceed as follows.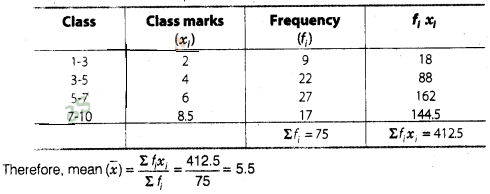

Hence, mean of the given distribution is 5.5.

Question 2:
Calculate the mean of the scores of 20 students in a mathematics test

Solution:
We first, find the class mark of each class and then proceed as follows

Hence, the mean of scores of 20 students in mathematics test is 35.

Question 3:
Calculate the mean of the following data

Solution:
Since, given data is not continuous, so we subtract 0.5 from the lower limit and add 0.5 in the upper limit of each class.
Now, we first find the class mark x_i, of each class and then proceed as follows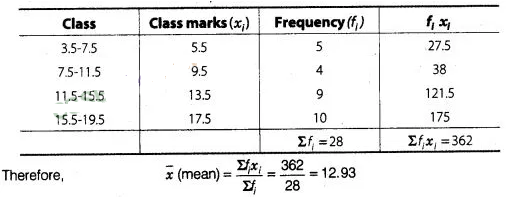

Hence, mean of the given data is 12.93.

Question 4:
The following table gives the number of pages written by Sarika for completing her own book for 30 days.

Find the mean number of pages written per day.
Solution:
Since,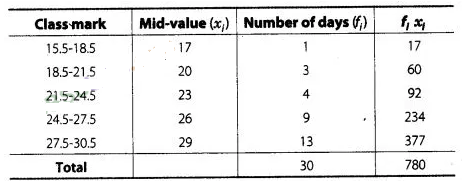

Since, given data is not continuous, so we subtract 0.5 from the lower limit and add 0.5 in the upper limit of each class.

Hence, the mean of pages written per day is 26.

Question 5:
The daily income of a sample of 50 employees are tabulated as follows.

Find the mean daily income of employees.
Solution:
Since, given data is not continuous, so we subtract 0.5 from the lower limit and add 0.5 in the upper limit of each class.
Now we first, find the class mark x_i, of each class and then proceed as follows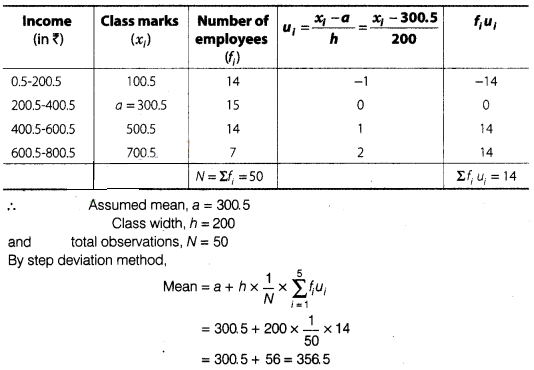

Question 6:
An aircraft has 120 passenger seats. The number of seats occupied during 100 flights is given in the following table.

Determine the mean number of seats occupied over the flights.
Solution:
We first, find the class mark x_i, of each class and then proceed as follows.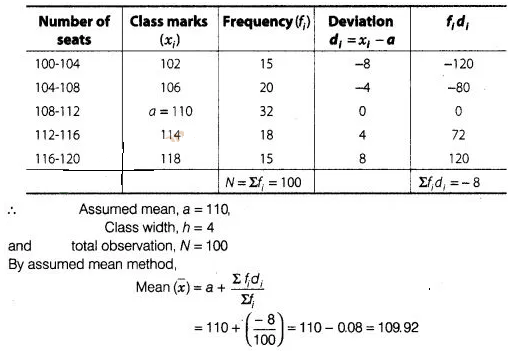

Question 7:
The weights (in kg) of 50 wrestlers are recorded in the following table.
Find the mean weight of the wrestlers.

Solution:
We first find the class mark of each class and then proceed as follows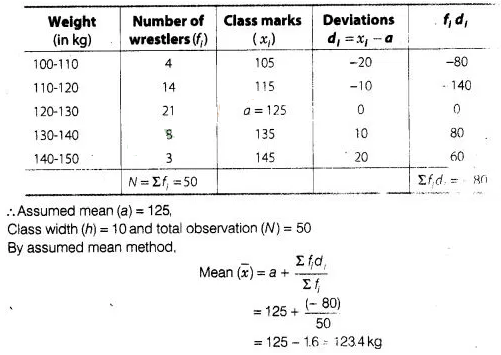

Question 8:
The mileage (km per litre) of 50 cars of the same model was tested by a manufacturer and details are tabulated as given below

Find the mean mileage.
The manufacturer claimed that the mileage of the model was 16 kmL ^-1.
Do you agree with this claim?
Solution: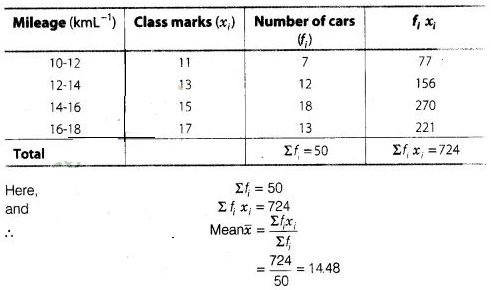

Hence, mean mileage is 14.48 kmL^-1.
No, the manufacturer is claiming mileage 1.52 kmh^-1 more than average mileage.

Question 9:
The following is the distribution of weights (in kg) of 40 persons.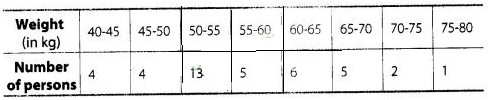

Construct a cumulative frequency distribution (of the less than type) table for the data above.
Solution:
The cumulative distribution (less than type) table is shown below

Question 10:
The following table shows the cumulative frequency distribution of marks of 800 students in an examination.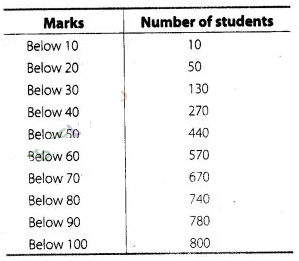

Construct a frequency distribution table for the data above.
Solution:
Here, we observe that 10 students have scored marks below 10 i.e., it lies between class interval 0-10. Similarly, 50 students have scored marks below 20. So, 50 -10 = 40 students lies in the interval 10-20 and so on. The table of a frequency distribution for the given data is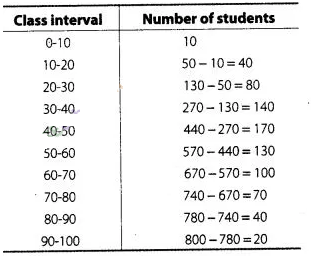

Question 11:
From the frequency distribution table from the following data.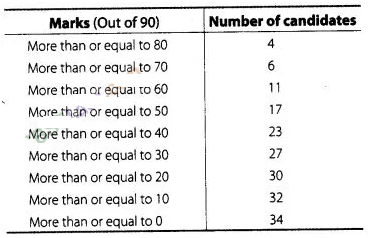

Solution:
Here, we observe that, all 34 students have scored marks more than or equal to 0. Since, 32 students have scored marks more than or equal to 10. So, 34- 32 =2 students lies in the interval 0-10 and so on.
Now, we construct the frequency distribution table.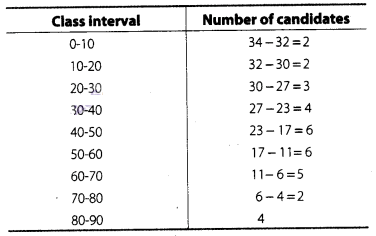

Question 12:
Find the unknown entries o, b, c, d, e and f in the following distribution of heights of students in a class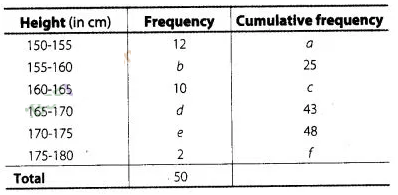

Solution: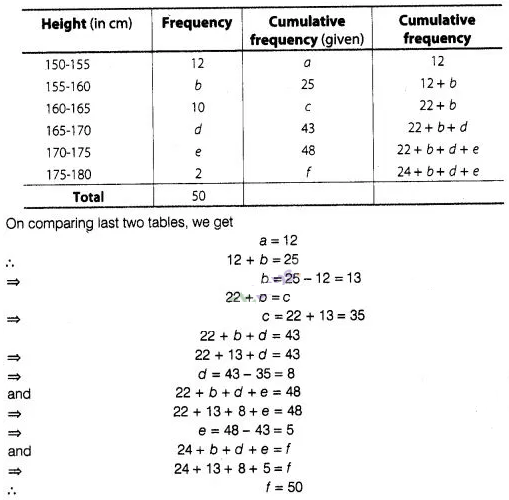

Question 13:
The following are the ages of 300 patients getting medical treatment in a hospital on a particular day

Form
(i) less than type cumulative frequency distribution.
(ii) More than type cumulative frequency distribution.
Solution:
(i) We observe that the number of patients which take medical treatment in a hospital on a particular day less than 10 is O’. Similarly, less than 20 include the number of patients which take medical treatment from 0-10 as well as the number of patients which take medical treatment from 10-20.
So, the total number of patients less than 20 is 0 + 60 = 60, we say that the cumulative frequency of the class 10-20 is 60. Similarly, for other class.
(ii) Also, we observe that all 300 patients which take medical treatment more than or equal to 10. Since, there are 60 patients which take medical treatment in the interval 10-20, this means that there are 300 – 60 = 240 patients which take medical treatment more than or equal to 20. Continuing in the same manner.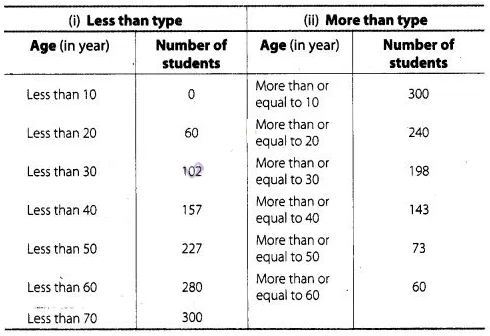

Question 14:
Given below is a cumulative frequency distribution showing the marks secured by 50 students of a class

Form the frequency distribution table for the data.
Solution:
Here, we observe that, 17 students have scored marks below 20 i.e., it lies between class interval 0-20 and 22 students have scored marks below 40, so 22 -17 = 5 students lies in the class interval 20-40 continuing in the same manner, we get the complete frequency distribution table for given data.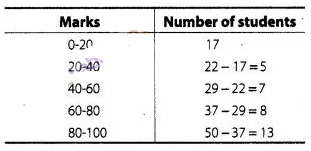

Question 15:
Weekly income of 600 families is tabulated below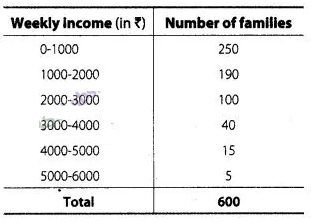

Compute the median income.
Solution:
First we construct a cumulative frequency table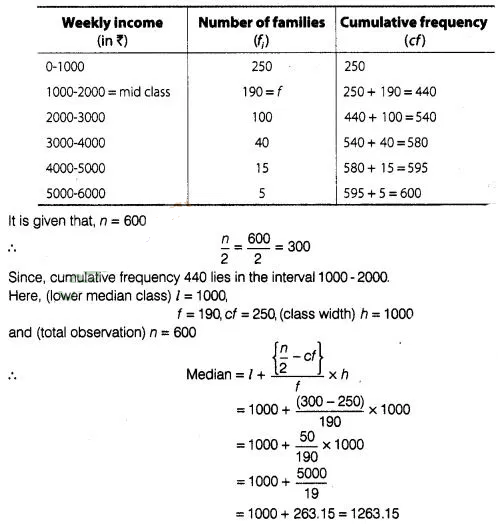

Hence, the median income is  ₹ 1263.15.

Question 16:
The maximum bowling speeds, in km per hour, of 33 players at a cricket coaching centre are given as follows

Caluculate the median bowling speed.
Solution:
First we construct the cumulative frequency table

Hence, the median bowling speed is 109.17 km/h.

Question 17:
The monthly income of 100 families are given as below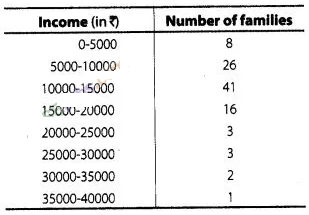

Caluculate the model income.
Solution:
In a given data, the highest frequency is 41, which lies in the interval 10000-15000.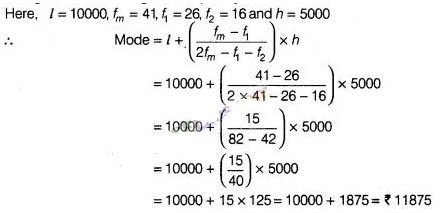

Hence, the modal income is  ₹ 11875.

Question 18:
The weight of coffee in 70 packets are shown in the following table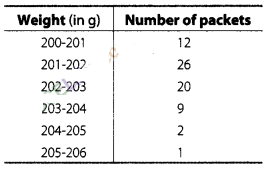

Determine the model weight .
Solution:
In the given data, the highest frequency is 26, which lies in the interval 201-202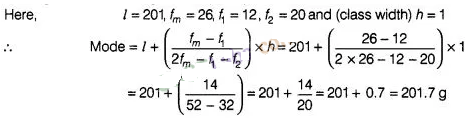

Hence, the modal weight is 201.7 g.

Question 19:
Two dice are thrown at the same time. Find the probability of getting
(i)  same number on both dice.
(ii) different number on both dice.
Solution:
Two dice are thrown at the same time.                                                                                     [given]
So, total number of possible outcomes = 36
(i) We have, same number on both dice.
So, possible outcomes are (1,1), (2, 2), (3, 3), (4, 4), (5, 5) and (6, 6).

(ii) We have, different number on both dice.
So, number of possible outcomes

Question 20:
Two dice are thrown simultaneously. What is the probability that the sum of the numbers appearing on the dice is
(i) 7 ?                                     (ii) a prime number ?                               (iii) 1 ?
Solution:
Two dice are thrown simultaneously.                                                                                      [given]
So, total number of possible outcomes = 36

Question 21:
Two dice are thrown together. Find the probability that the product of the numbers on the top of the dice is
(i) 6                             (ii) 12                         (iii) 7
Solution:
Number of total outcomes = 36

Question 22:
Two dice are thrown at the same time and the product of numbers appearing on them is noted. Find the probability that the product is less than 9.
Solution:
Number of total outcomes = 36
When product of numbers appearing on them is less than 9, then possible ways are (1,6), (1,5) (1,4), (1,3), (1,2), (1,1), (2, 2), (2, 3), (2, 4), (3, 2), (4, 2), (4,1), (3,1), (5,1), (6,1) and (2,1).
Number of possible ways = 16
Required probability = \(\frac{16}{36} = \frac{4}{9}\)

Question 23:
Two dice are numbered 1, 2, 3, 4, 5, 6 and 1, 1, 2, 2, 3, 3, respectively. They are thrown and the sum of the numbers on them is noted. Find the probability of getting each sum from 2 to 9, separately.
Solution:
Number of total outcomes = 36

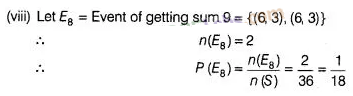
Question 24:
A coin is tossed two times. Find the probability of getting atmost one head.
Solution:
The possible outcomes,if a coin is tossed 2 times is

Question 25:
A coin is tossed 3 times. List the possible outcomes. Find the probability of getting
(i) all heads                                (ii) atleast 2 heads
Solution:
The possible outcomes if a coin is tossed 3 times is
S = {(HHH), (TTT), (HTT), (THT), (TEH), (THH), (HTH), (HHT)}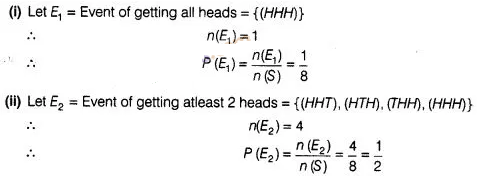

Question 26:
Two dice are thrown at the same time. Determine the probability that the difference of the numbers on the two dice is 2.
Solution:
The total number of sample space in two dice, n (S) = 6 x 6 = 36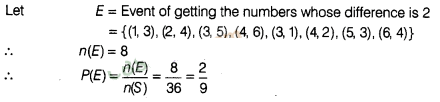

Question 27:
A bag contains 10 red, 5 blue and 7 green balls. A ball is drawn at random. Find the probability of this ball being a
(i) red ball                          (ii) green ball                         (iii) not a blue ball
solution:
if a ball is drawn out of 22 balls (5 blue + 7 green + 10 red), then the total number of outcomes are

Question 28:
The king, queen and jack of clubs are removed from a deck of 52 playing cards and then well shuffled. Now, one card is drawn at fandom from the remaining cards. Determine the probability that the card is
(i) a heart                                        (ii) a king
Solution:
If we remove one king, one queen and one jack of clubs from 52 cards, then the remaining
cards left, n(S) = 49

Question 29:
Refer to Q.28. What is the probability that the card is
(i) a club                                (ii) 10 of hearts
Solution:

Question 30:
All the jacks, queensapd kings are removed from a deck of 52 playing cards. The remaining cards are well shuffled and then one card is drawn at random. Giving ace a value 1 similar value for other cards, find the probability that the card has a value.
(i) 7                                              (ii) greater than 7                                             (iii) Less than 7
Solution:
In out of 52 playing cards, 4 jacks, 4 queens and 4 kings are removed, then the remaining
cards are left, n(S) = 52 – 3 x 4 = 40.

Question 31:
An integer is chosen between 0 and 100. What is the probability that it is
(i) divisible by 7?                          (ii) not divisible by 7?
Solution:
The number of integers between 0 and 100 is
n(S)= 99

Question 32:
Cards with numbers 2 to 101 are placed in a box. A card is selected at random. Find the probability that the card has
(i) an even number                                           (ii) a square number                 ‘
Solution:
Total number of out comes with numbers 2 to 101, n(s) =100

Question 33:
A letter of english alphabets is chosen at random. Determine the probability that the letter is a consonant
Solution:
We know that, in english alphabets, there are (5 vowels + 21 consonants)=26 letters. So,
total number of outcomes in english alphabets are,                                                                                               
n(S) = 26

Question 34:
There are 1000 sealed envelopes in a box, 10 of them contain a cash prize of  ₹ 100 each, 100 of them contain a cash prize of  ₹ 50 each and 200 of them contain a cash prize of  ₹ 10 each and rest do not contain any cash prize. If they are well shuffled and an envelope is picked up out, what is the probability that it contains no cash prize?
Solution:
Total number of sealed envelopes in a box, n (S) = 1000
Number of envelopes containing cash prize = 10 + 100 + 200 = 310
Number of envelopes containing no cash prize,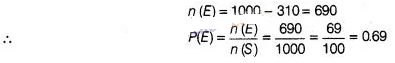

Question 35:
Box A contains 25 slips of which 19 are marked  ₹ 1 and other are marked  ₹ 5 each. Box B contains 50 slips of which 45 are marked  ₹ 1 each and others are marked  ₹ 13 each. Slips of both boxes are poured into a third box and resuffled. A slip is drawn at random. What is the probability that it is marked other than  ₹ 1?
Solution:
Total number of slips in a box, n(S) = 25 + 50 = 75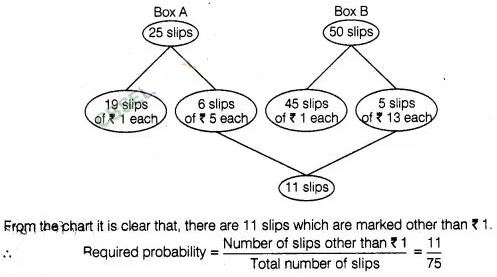

Question 36:
A carton of 24 bulbs contain 6 defective bulbs. One bulb is drawn at random. What is the probability that the bulb is not defective? If the bulb selected is defective and it is not replaced and a second bulb is selected at random from the rest, what is the probability that the second bulb is defective?
Solution:
∴Total number of bulbs, n (S) = 24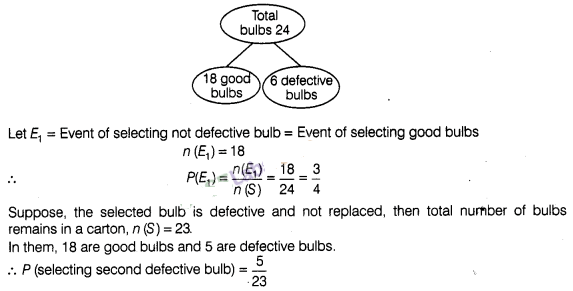

Question 37:
A child’s game has 8 triangles of which 3 are blue and rest are red, and 10 squares of which 6 are blue and rest are red. One piece is lost at random. Find the probability that it is a
(i) triangle                       (ii) square                         (iii)square of blue colour                       (iv) triangle of red colour
Solution:

Question 38:
In a game, the entry fee is of  ₹ 5. The game consists of a tossing a coin 3 times. If one or two heads show, Sweta gets her entry fee back. If she throws 3 heads, she receives double the entry fees. Otherwise she will lose. For tossing a coin three times, find the probability that she
(i)   loses the entry fee.
(ii)  gets double entry fee.
(iii) just gets her entry fee.
Solution:
Total possible outcomes of tossing a coin 3 times,
S = {(HHH), (TTT), (HTT), (THT), (TTH), (THH), (HTH), (HHT)}
∴                                                        n (S) = 8

Question 39:
A die has its six faces marked 0, 1, 1, 1, 6, 6. Two such dice are thrown together and the total score is recorded.
(i)  How many different scores are possible?
(ii) What is the probability of getting a total of 7?
Solution:
Given, a die has its six faces marked {0,1,1,1,6, 6}
Total sample space, n(S) = 6² = 36
(i) The different score which are possible are 6 scores e., 0,1,2,6,7 and12.
(ii) Let E = Event of getting a sum 7

Question 40:
A lot consists of 48 mobile phones of which 42 are good, 3 have only minor defects and 3 have major defects. Varnika will buy a phone, if it is good but the trader will only buy a mobile, if it has no major defect. One phone is selected at random from the lot. What is the probability that it is
(i)  acceptable to Varnika?
(ii) acceptable to the trader?
Solution: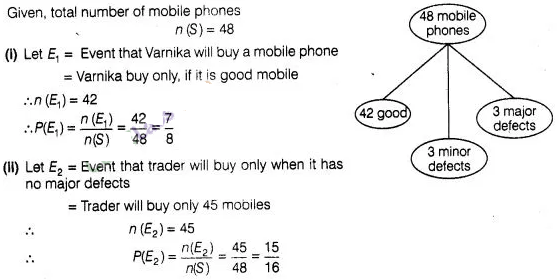

Question 41:
A bag contains 24 balls of which x are red, 2x are white and 3x am are. A ball is selected at random. What is the probability that it
(i) not red?                                   (ii) white
Solution:
Given that, A bag contains total number of balls = 24 A bag contains number of red bails = 24
A bag contains number of white balls = 2x and a bag contains number of blue balls = x
By condition,                    x + 2x + 3x = 24
⇒                                                         6x = 24
∴                                                            x =  4
∴Number of red balls = x = 4
Number of white balls = 2x = 2 x 4 = 8
and number of blue balls = 3x = 3 x 4 = 12
So, total number of outcomes for a ball is selected at random in a bag contains 24 balls.
⇒                                                                 n(S) = 24

Question 42:
At a fete, cards bearing numbers 1 to 1000, one number on one card, are put in a box. Each player selects one card at random and that card is not replaced. If the selected card has a perfect square greater than 500, the player wins a prize. What is the probability that
(i)  the first player wins a prize?
(ii) the second player wins a prize, if the first has won?
Solution:
Given that,, at a fete, cards bearing numbers 1 to 1000 one number on one card, are put in a box. Each player selects one card at random and that card is not replaced so, the total number of outcomes are n(S) = 1000
If the selected card has a perfect square greater than 500, then player wins a prize.

Exercise 13.4 Long Answer Type Questions

Question 1:
Find the mean marks of students for the following distribution

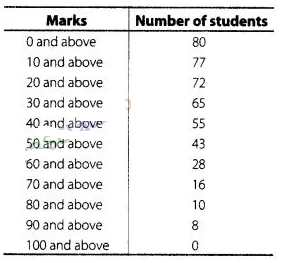
Solution: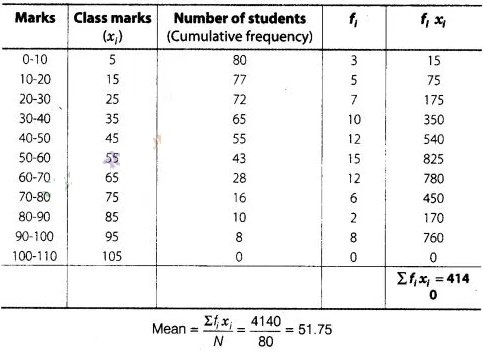

Question 2: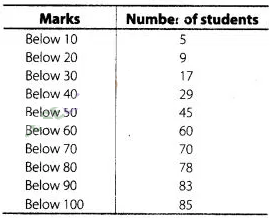

Solution:
Here, we observe that, 5 students have scored marks below 10, i.e. it lies between class interval 0-10 and 9 students have scored marks below 20,
So, (9 – 5) = 4 students lies in the class interval 10-20. Continuing in the same manner, we get the complete frequency distribution table for given data.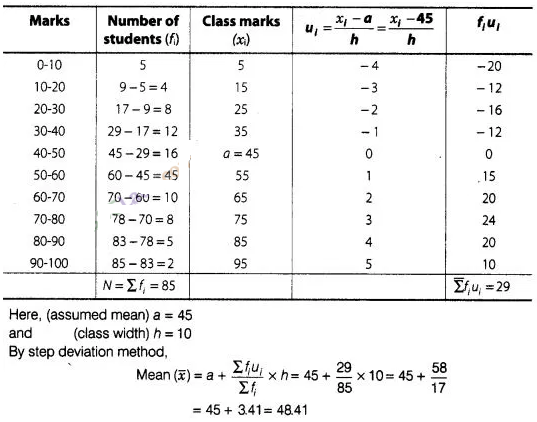

Question 3:
Find the mean age of 100 residents of a town from the following data.

Solution:
Here, we observe that, all 100 residents of a town have age equal and above 0. Since, 90 residents of a town have age equal and above 10.
So, 100 – 90 = 10 residents lies in the interval 0-10 and so on. Continue in this manner, we get frequency of all class intervals. Now, we construct the frequency distribution table.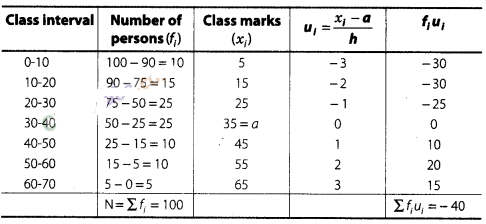

Question 4:
The weights of tea in 70 packets are shown in the following table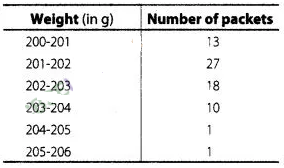

Find the mean weight of packets.
Solution:
First,we find the class marks of the given data as follows,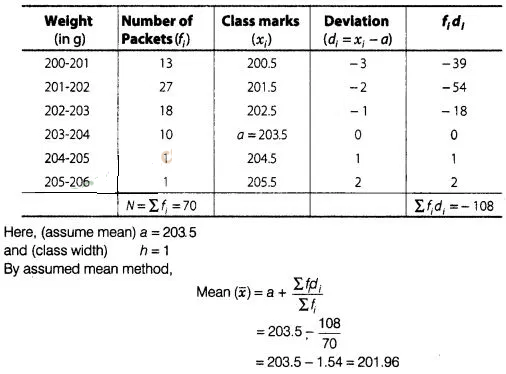

Hence, the required mean weight is 201.96 g.

Question 5:
Refer to Q.4 above. Draw the less than type ogive for this data and use it to find the median weight.
Solution:
We observe that, the number of packets less than 200 is 0, Similarly, less than 201 include the number of packets from 0-200 as well as the number of packets from 200-201.
So, the total number of packets less than 201 is 0 + 13 = 13. We say that, the cumulative frequency of the class 200-201 is 13. Similarly, for other class.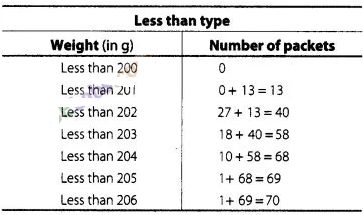

To draw the less than type ogive, we plot the points (200, 0), (201, 13), (202, 40) (203, 58), (204, 68), (205, 69) and (206, 70) on the paper and join by free hand, v Total number of packets (n) = 70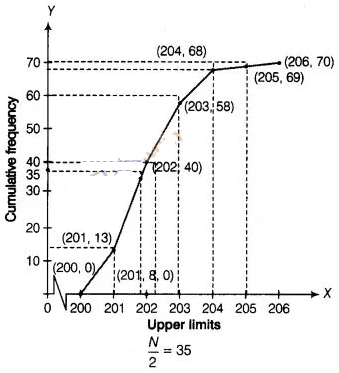

Firstly, we plot a point (0, 35) on Y-axis and draw a line y = 35 parallel to X-axis. The line cuts the less than ogive curve at a point. We draw a line on that point which is perpendicular to X-axis. The foot of the line perpendicular to X-axis is the required median.
Median weight = 201.8 g

Question 6:
Refer to Q.5 above. Draw the less than type and more than type ogives for the data and use them to find the meadian weight.
Solution:
For less than type table we follow the Q.5.
Here, we observe that, the weight of all 70 packets is more than or equal to 200. Since, 13 packets lie in the interval 200-201. So, the weight of 70 -13 = 57 packets is more than or equal to 201. Continuing in this manner we will get remaining more than or equal to 202, 203, 204, 205 and 206.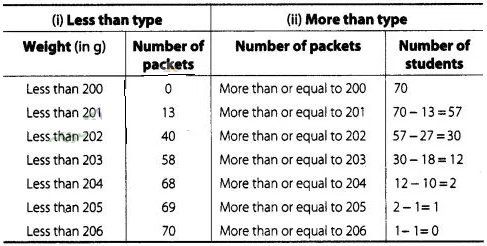

To draw the less than type ogive, we plot the points (200, 0), (201,13), (202, 40), (203, 58), (204, 68), (205,69), (206, 70) on the paper and join them by free hand.
To draw the more than type ogive plot the points (200, 70), (201, 57), (202, 30), (203, 12), (204, 2), (205,1), (206, 0) on the the graph paper and join them by free hand.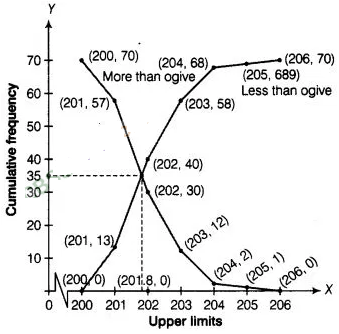

Hence,required median weight = intersection point of x – axis = 201.8 g.

Question 7:
The table below shows the salaries of 280 persons.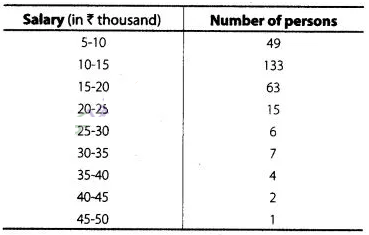

caluculate the median and mode of the data.
Solution:
First, we construct a cumulative frequency table.


Hence,the median and modal salary are ₹13421 and ₹12727,respetively.

Question 8:
The mean of the following frequency distribution is 50 but the frequencies f₁ and f₂ in classes 20-40 and 60-80, respectively are not known. Find these frequencies, if the sum of all the frequencies is 120.

Solution:
First we caluculate the class mark of given data

Question 9:
The median of the following data is 50. Find the values of p and q, if the sum of all the frequencies is 90.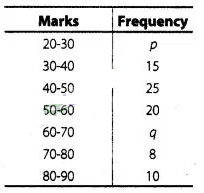

Solution:.

Question 10:
The distribution of heights (in cm) of 96 children is given below

Draw a less than type cumulative frequency curve for this data and use it to compute median height of the children.
Solution: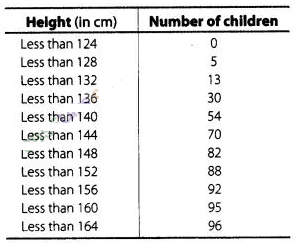

To draw the less than type ogive, we plot the points (124, 0), (128, 5), (132, 13), (136, 30), (140, 54), (144, 70), (148, 82), (152, 88), (156, 92), (160, 95), (164, 96) and join all these point by free hand.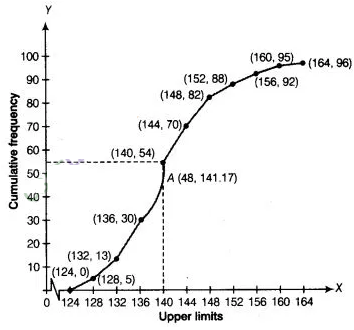

Here,                                        \(\frac{N}{2} =\frac{96}{2}\)
We take, y = 48 in Y-coordinate and draw a line parallel to X-axis, meets the curve at A and draw a perpendicular line from point A to the X-axis and this line meets the X-axis at the point which is the median i.e., median = 141.17.

Question 11:
Size of agricultural holdings in a survey of 200 families is given in the following
Compute median and mode size of the holdings.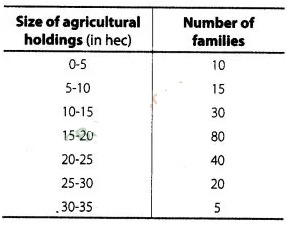

Solution: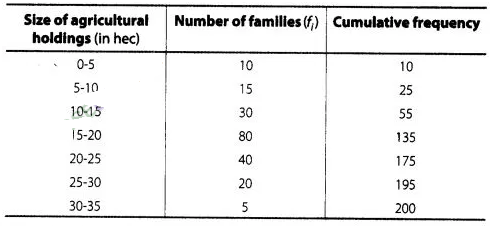

Question 12:
The annual rainful record of a city for 66 days is given in the following table.

Calculate the median rainfall using ogives (or move than type and of less than type)
Solution:
We observe that, the annual rainfall record of a city less than 0 is 0. Similarly, less than 10 include the annual rainfall record of a city from 0 as well as the annual rainfall record of a city from 0-10._v
So, the total annual rainfall record of a city for less than 10 cm is 0+ 22 =22 days. Continuing in this manner, we will get remaining less than 20, 30, 40, 50, and 60.
Also, we observe that annual rainfall record of a city for 66 days is more than or equal to 0 cm. Since, 22
days lies in the interval 0-10. So, annual rainfall record for 66-22 = 44days is more than or equal to 10 cm.
Continuing in this manner we will get remaining more than or equal to 20, 30, 40, 50 and 60.
Now, we construct a table for less than and more than type.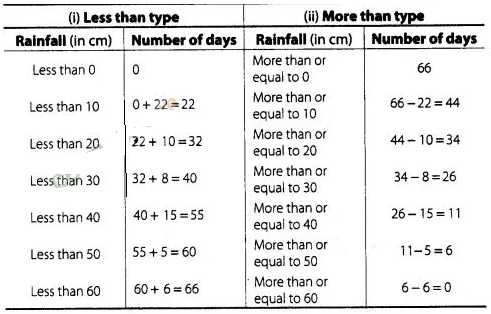

To draw less than type ogive we plot the points (0, 0), (10, 22), (20, 32), (30, 40), (40, 55), (50, 60), (60, 66) on the paper and join them by free hand.
To draw the more than type ogive we plot the points (0, 66), (10, 44), (20, 34), (30, 26), (40, 11), (50, 6) and (60, 0) on the graph paper and join them by free hand,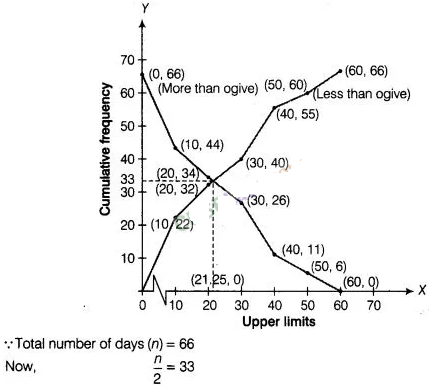

Firstly, we plot a line parallel to X-axis at intersection point of both ogives, which further intersect at (0, 33) on Y-axis. Now, we draw a line perpendicular to X-axis at intersection point of both ogives, which further intersect at (21.25, 0) on X-axis. Which is the required median using ogives.
Hence, median rainfall = 21.25 cm.

Question 13:
The following is the frequency distribution of duration for 100 calls made on a mobile phone.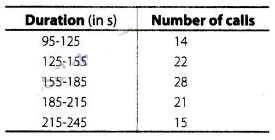

Solution:
First, we calculate class marks as follows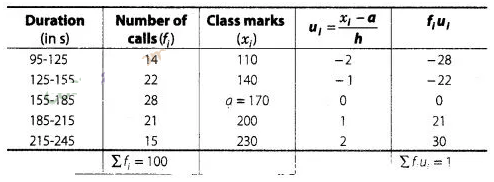

Here, (assumed mean) a = 170,
and (class width) h = 30
By step deviation method,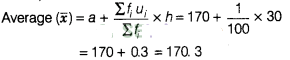

Hence, average duration is 170.3s.
For calculating median from a cumulative frequency curve
We prepare less than type or more than type ogive
We observe that, number of calls in less than 95 s is 0. Similarly, in less than 125 s include the number of calls in less than 95 s as well as the number of calls from 95-125.s So, the total number of calls less than 125 s is 0 + 14 = 14. Continuing in this manner, we will get remaining in less than 155,185, 215 and 245 s.
Now, we construct a table for less than ogive (cumulative frequency curve).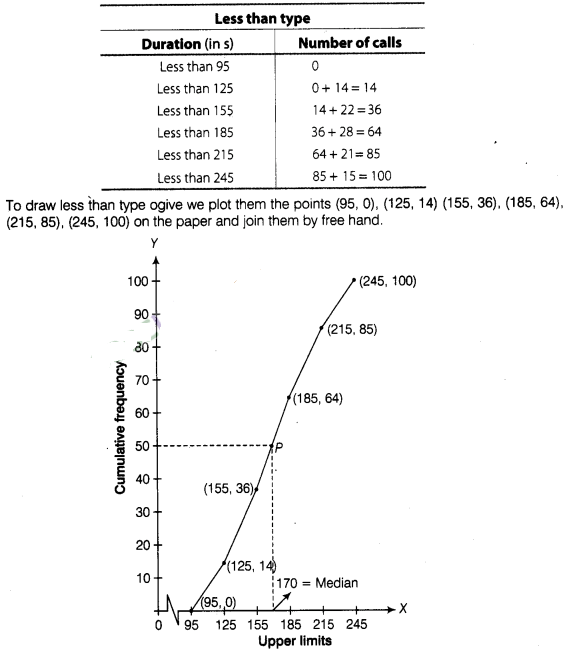


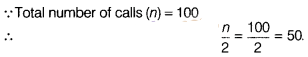
Now, point 50 taking on Y-axis draw a line parallel to X-axis meet at a point P and draw a perpendicular line from P to the X-axis, the intersection point of X-axis is the median.
Hence, required median is 170 .

Question 14:
50 students enter for a school javelin throw competition. The distance (in metre) thrown are recorded below

(i)   Construct a cumulative frequency table.
(ii)  Draw a cumulative frequency curve (less than type) and calculate the median distance drawn by using
this curve.
(iii) Calculate the median distance by using the formula for median.
(iv) Are the median distance calculated in (ii) and (iii) same?
Solution: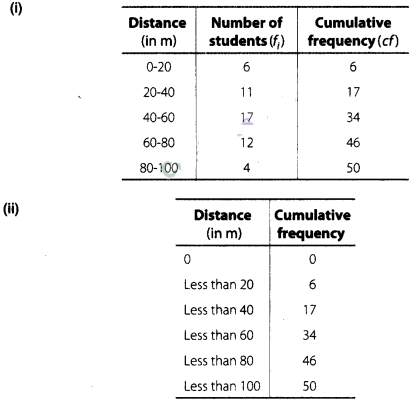

To draw less than type ogive, we plot the points (0, 0), (20, 6), (40,17), (60, 34), (80, 46), (100, 50), join all these points by free hand.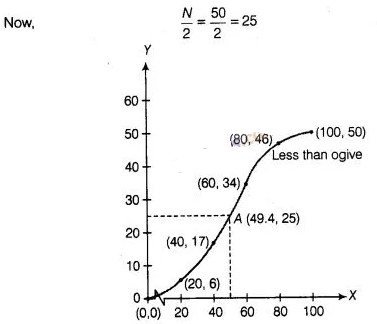

Taking Y = 25 on y-axis and draw a line parallel to X-axis, which meets the curve at point A From point A we draw a line perpendicular to X-axis, where this meets that point is the required median i.e., 49.4.

(lv) Yes, median distance calculated by parts (ii) and (iii) are same.