Chapter 11 Area Related To Circles

NCERT Exemplar Problems Class 10 Maths Solutions Chapter 11 Area Related To Circles

Exercise 11.1 Multiple Choice Questions (MCQs)

Question 1:
If the sum of the areas of two circles with radii R₁ and R₂ is equal to the area of a circle of radius R, then

Solution:
(b) According to the given condition,
                                                          Area of circle =Area of first circle + Area of second circle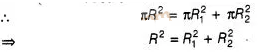

Question 2:
If the sum of the circumferences of two circles with radii R₁ and R₂ is equal to the circumference of a circle of radius R, then
(a) R₁ + R₂=R
(b) R₁ + R₂ > R
(c) R₁ + R₂ < R
(d) Nothing definite can be said about the relation among R_1,R₂ and R
Solution:
(a) According to the given condition,
Circumference of circle = Circumference of first circle + Circumference of second circle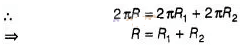

Question 3:
If the circumference of a circle and the perimeter of a square are equal, then
(a) Area of the circle = Area of the square
(b) Area of the circle > Area of the square
(c) Area of the circle < Area of the square
(d) Nothing definite can be said about the relation between the areas of the circle and square
Solution:
(b) According to the given condition,
Circumference of a circle = Perimeter of square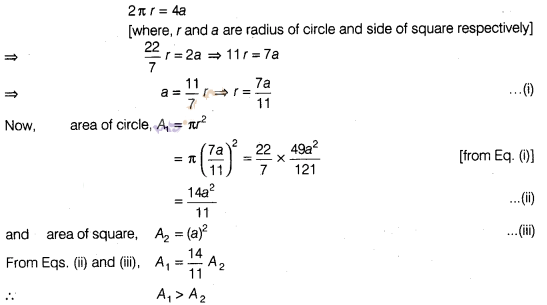

Hence, Area of the circle > Area of the square.

Question 4:
Area of the largest triangle that can be inscribed in a semi-circle of radius r units is
(a) r² squnits                  (b) \(\frac { 1 }{ 2 } \) r² sq units                  (c) 2r² sq units                              (d) √2 r² sq units
Solution:
(a) Take a point C on the circumference of the semi-circle and join it by the end points of diameter A and B.

Question 5:
If the perimeter of a circle is equal to that of a square, then the ratio of their areas is
(a) 22 :7                     (b) 14:11                   (c) 7:22                      (d) 11:14
Solution:
(b) Let radius of circle be r and side of a square be a.
According to the given condition,

Question 6:
It is proposed to build a single circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park would be
(a) 10 m                    (b)15m                       (c) 20 m                     (d) 24 m
Solution:
(a) Area of first circular park, whose diameter is 16 m

Question 7:
The area of the circle that can be inscribed in a square of side 6 cm is
(a) 36π cm²                 (b) 18π cm²                       (c) 12π cm²                            (d) 9π cm²
Solution:

Question 8:
The area of the square that can be inscribed in a circle of radius 8 cm is
(a) 256 cm²               (b) 128 cm²               (c)64√2 cm²             (d)64 cm²
Solution:
(b) Given, radius of circle, r = OC = 8cm.
∴ Diameter of the circle = AC = 2 x OC = 2 x 8= 16 cm
which is equal to the diagonal of a square.
Let side of square be x.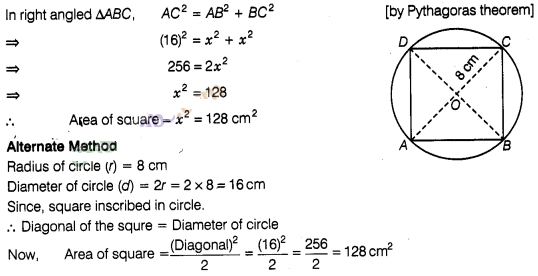

Question 9:
The radius of a circle whose circumference is equal to the sum of the circumferences of the two circles of diameters 36 cm and 20 cm is
(a) 56 cm                             (b) 42 cm                             (c) 28 cm                               (d) 16 cm
Solution:
(c) ∵ Circumference of first circle = 2 πr = πd₁ = 36 π cm                                  [given, d₁ = 36 cm]
and circumference of second circle = πd₂ = 20 π cm                                 [given, d₂ = 20 cm]
According to the given condition,
Circumference of circle = Circumference of first circle + Circumference of second circle

Question 10:
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is
(a) 31 cm                   (b) 25 cm                   (c) 62 cm                   (d) 50 cm
Solution:
(d) Let r₁ = 24 cm and r₂ = 7 cm

Exercise 11.2 Very Short Answer Type Questions

Write whether True or False and justify your answer

Question 1:
Is the area of the circle inscribed in a square of side a cm, πa² cm² ? Give reasons for your answer
Solution:
False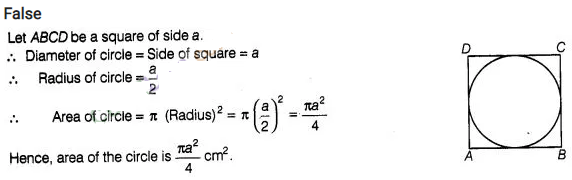

Question 2:
Will it be true to say that the perimeter of a square circumscribing a circle of radius a cm is 80 cm? Give reason for your answer.
Solution:

Question 3:
In figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give reason for your answer.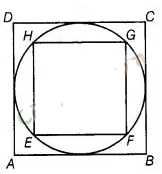

Solution:
False
Given diameter of circle is d.
∴ Diagonal of inner square = Diameter of circle = d
Let side of inner square EFGH be x.
∴ In right angled ΔEFG,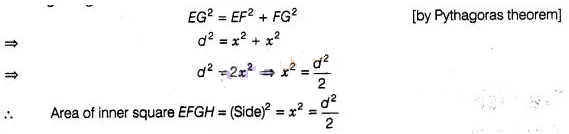

But side of the outer square ABCS = Diameter of circle = d
∴                                                 Area of outer square = d²
Hence, area of outer square is not equal to four times the area of the inner square.

Question 4:
Is it true to say that area of segment of a circle is less than the area of its corresponding sector? Why?
Solution:
False
It is true only in the case of minor segment. But in case of major segment area is always greater than the area of sector.

Question 5:
Is it true that the distance travelled by a circular wheel of diameter d cm in one revolution is 2πd cm? Why?
Solution:
False
Because the distance travelled by the wheel in one revolution is equal to its circumference i.e., πd.
i.e.,                                π(2r) = 2 πr = Circumference of wheel                                   [∵d = 2r]

Question 6:
In covering a distance s m, a circular wheel of radius r m makes \(\frac{s}{2\pi r}\)
revolution. Is this statement true? Why?
Solution:
True
The distance covered in one revolution is 2πr i.e., its circumference.

Question 7:
The numerical value of the area of a circle is greater than the numerical value of its circumference. Is this statement true? Why?
Solution:
False
If 0< r< 2, then numerical value of circumference is greater than numerical value of area of circle and if r > 2, area is greater than circumference.

Question 8:
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
Solution:
False
Let two circles C₁ and C₂ of radius r and 2r with centres O and O’, respectively.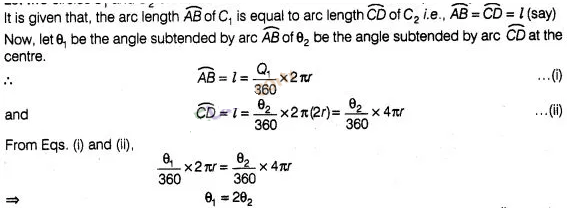

i.e., angle of the corresponding sector of C₁ is double the angle of the corresponding sector of C₂.
It is true statement

Question 9:
The area of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
Solution:
False
It is true for arcs of the same circle. But in different circle, it is not possible.

Question 10:
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
Solution:
False
It is true for arcs of the same circle. But in different circle, it is not possible

Question 11:
Is the area of the largest circle that can be drawn inside a rectangle of length a cm and breadth b cm (a > b) is π b² cm? Why?
Solution:
False
The area of the largest circle that can be drawn inside a rectangle is π ( \(\frac { b }{ 2 } \) )² cm, where π \(\frac { b }{ 2 } \) is the radius of the circle and it is possible when rectangle becomes a square.

Question 12:
Circumference of two circles are equal. Is it necessary that their areas be equal? Why?
Solution:
True
If circumference of two circles are equal, then their corresponding radii are equal. So, their areas will be equal.

Question 13:
Areas of two circles are equal. Is it necessary that their circumferences are equal? Why?
Solution:
True
If areas of two circles are equal, then their corresponding radii are equal. So, their circumference will be equal.

Question 14:
Is it true to say that area of a square inscribed in a circle of diameter p cm is p² cm² ? Why?
Solution:
True
When the square is inscribed in the circle, the diameter of a circle is equal to the diagonal of a square but not the side of the square.

Exercise 11.3 Short Answer Type Questions

Question 1:
Find the radius of a circle whose circumference is equal to the sum of the circumference of two circles of radii 15 cm and 18 cm.
Solution:
Let the radius of a circle be r.
∴              Circumference of a circle = 2πr
Let the radii of two circles are r₁ and r₂ whose values are 15 cm and 18 cm respectively.
i.e.         r₁ = 15cmand r₂ = 18cm
Now, by given condition,
Circumference of circle = Circumference of first circle + Circumference of second circle
⇒                    2πr = 2πr₁ + 2πr_2
⇒                                 r = r₁ + r_2
⇒                                 r = 15 + 18
∴                           r = 33 cm
Hence, required radius of a circle is 33 cm.

Question 2:
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.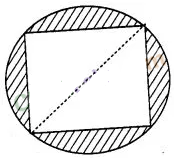

Solution:
Let the side of a square be a and the radius of circle be r.
Given that, length of diagonal of square = 8 cm

So, the area of the shaded region = Area of circle – Area of square
= (16π – 32) cm²
Hence, the required area of the shaded region is (16π – 32) cm².

Question 3:
Find the area of a sector of a circle of radius 28 cm and central angle 45°.
Solution:
Given that, Radius of a circle, r = 28 cm
and measure of central angle θ= 45°
Hence, the required area of a sector of a circle is 308 cm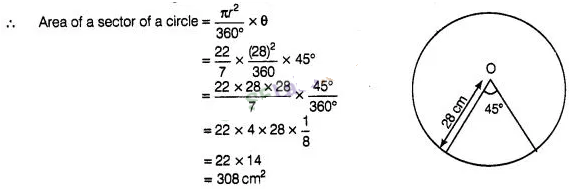

Question 4:
The wheel of a motor cycle is of radius 35 cm. How many revolutions per minute must the wheel make, so as to keep a speed of 66 km/h?
Solution:
Given, radius of wheel, r = 35 cm

Hence, required number of revolutions per minute is 500.

Question 5:
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m x 16 m. Find the area of the field in which the cow can graze.
Solution:
Let ABCD be a rectangular field of dimensions 20 m x 16 m . Suppose, a cow is tied at a point A Let length of rope be AE = 14 m = r (say).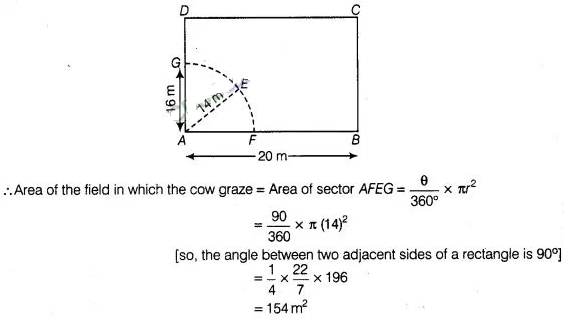

Question 6:
Find the area of the flower bed (with semi-circular ends) shown in figure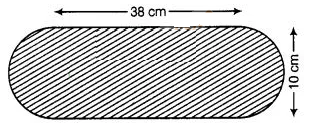

Solution:
Length and breadth of a circular bed are 38 cm and 10 cm.
∴                           Area of rectangle ACDF = Length x Breadth = 38 x 10 = 380 cm²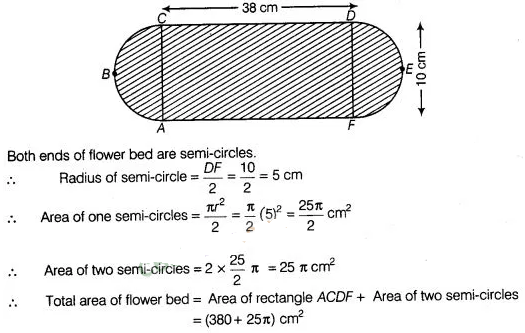

Question 7:
In figure, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region, (use π = 3.14)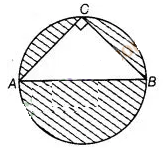

Solution:
Given,                                          AC = 6 cm and BC = 8 cm
We know that, triangle in a semi-circle with hypotenuse as diameter is right angled triangle.

Question 8:
Find the area of the shaded field shown in figure.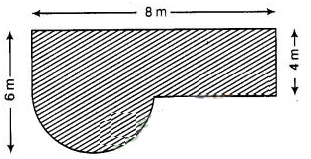

Solution:
In a figure, join ED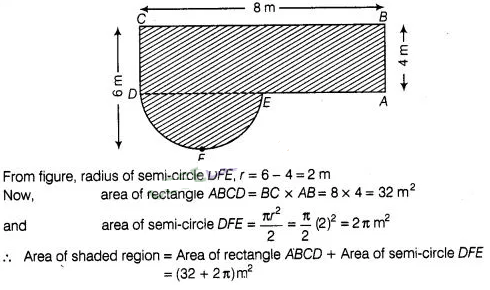

Question 9:
Find the area of the shaded region in figure.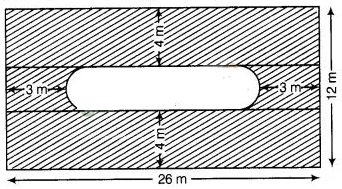

Solution:
join GH and FE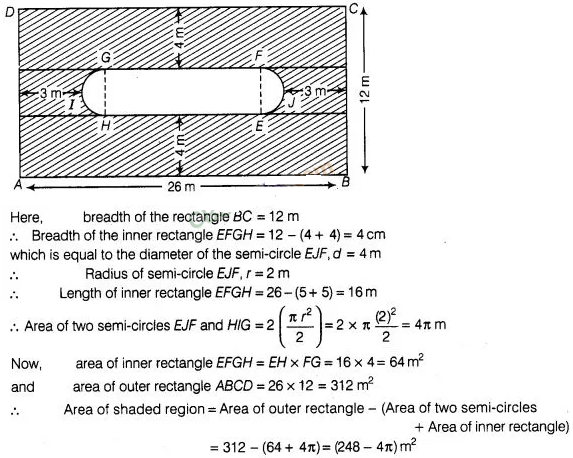

Question 10:
Find the area of the minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 60°.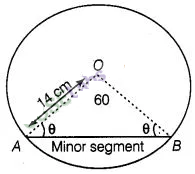

Solution:
Given that, radius of circle (r) = 14 cm
and angle of the corresponding sector i.e., central angle (θ) = 60°
Since, in ΔAOB, OA = OB = Radius of circle i.e., ΔAOB is isosceles.

Question 11:
Find the area of the shaded region in figure, where arcs drawn with centres A, B, C and D intersect in pairs at mid-point P, Q, R and 5 of the sides AB, BC, CD and DA, respectively of a square ABCD. (use π = 3.14)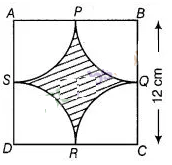

Solution:
Given, side of a square BC = 12 cm
Since, Q is a mid-point of BC.

Question 12:
In figure arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm, To intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region, (use π = 3.14)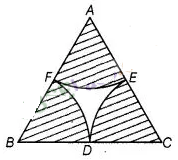

Solution:
Since, ABC is an equilateral triangle.

Question 13:
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.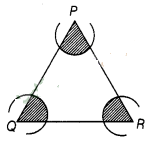

Solution:
Given that, radii of each arc (r) = 14 cm

Hence, the required  area of the shaded region is 308 cm².

Question 14:
A circular park is surrounded by a road 21 m wide. If the radius of the  park is 105 m, then find the area of the road.
Solution: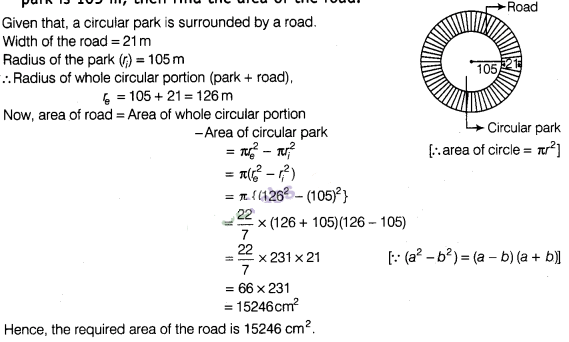

Question 15:
In figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.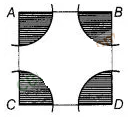

Solution:
Given that, radius of each arc (r) = 21 cm

Hence, required area of the shade region is 1386 cm²

Question 16:
A piece of wire 20 cm long is bent into the from of an arc of a circle, subtending an angle of 60° at its centre. Find the radius of the circle.
Solution:
Length of arc of circle = 20 cm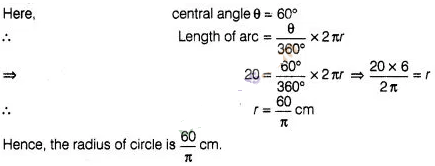

Exercise 11.4 Long Answer Type Questions

Question 1:
The area of a circular playground is 22176 m².Find the cost of fencing this ground at the rate of  ₹ 50 per m.
Solution:
Given, area of a circular playground = 22176 m²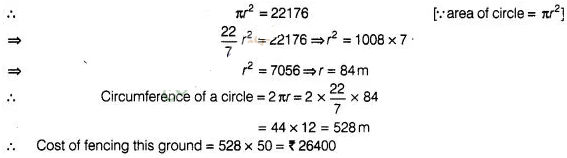

Question 2:
The diameters of front and rear wheels of a tractor are 80 cm and 2m, respectively. Find the number of revolutions that rear wheel will make in covering a distance in which the front wheel makes 1400 revolutions.
Solution:
Given, diameter of front wheels, d₁ = 80 cm
and diameter of rear wheels, d₂ = 2 m = 200 cm

Question 3:
Sides of a triangular field are 15 m, 16m and 17m. with the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7m each to graze in the field.
Find the area of the field which cannot be grazed by the three animals.
Solution:
Given that, a triangular field with the three corners of the field a cow, a buffalo and a horse are tied separately with ropes. So, each animal grazed the field in each corner of triangular field as a sectorial form.
Given, radius of each sector (r) = 7m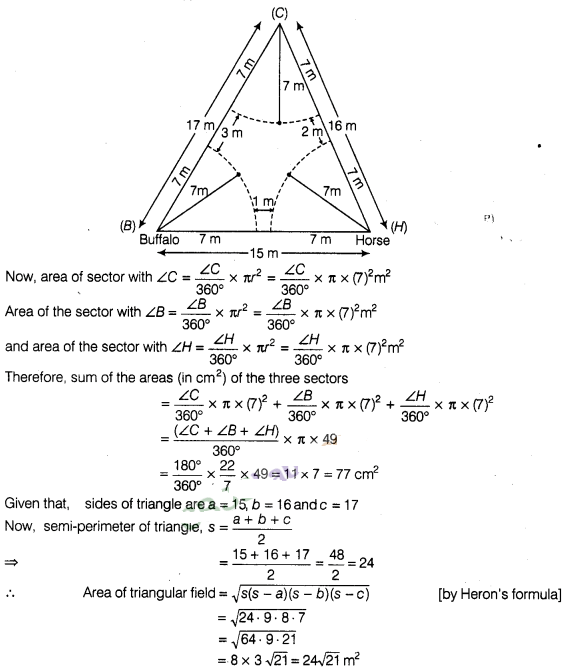

Question 4:
Find the area of the segment of a circle of radius 12 cm whose corresponding sector has a centrel angle of 60°. (use π = 3.14)
Solution:
Given that, radius of a circle (r) = 12 cm
and central angle of sector OBCA (θ) = 60°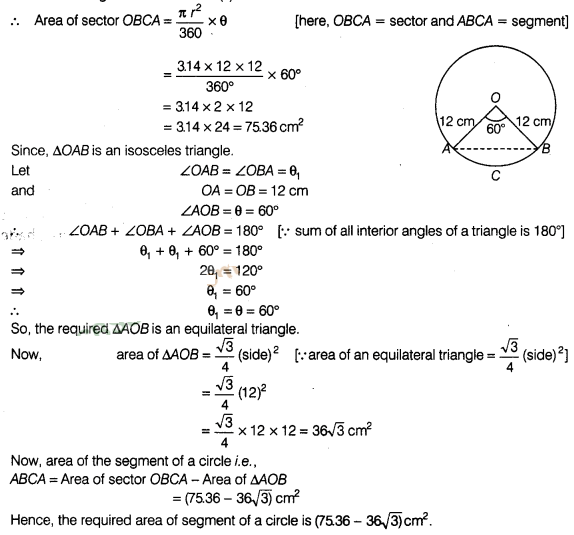

Question 5:
A circular pond is 17.5 m is of diameter. It is surrounded by a 2m wide path. Find the cost of constructing the path at the rate of  ₹ 25 Per m²?
Solution:
Given that, a circular pond is surrounded by a wide path.
The diameter of circular pond = 17.5 m

Question 6:
In figure, ABCD is a trapezium with AB || DC. AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.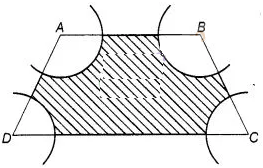

Solution:
Given, AB = 18 cm, DC = 32 cm, height, (h) = 14cm

Hence, the required area of shaded region is 1996 cm²

Question 7:
Three circles each of radius 3.5 cm are drawm in such a way that each of them touches the other two. Find the area enclosed between these circles.
Solution:
Given that, three circles are in such a way that each of them touches the other two.
Now, we join centre of all three circles to each other by a line segment. Since, radius of each circle is 3.5 cm.
So;                                             AB = 2 x Radius of circle
= 2 x 3.5 = 7 cm.
⇒                                               AC = BC = AB = 7cm
which shows that, ΔABC is an equilateral triangle with side 7 cm.
We know that, each angle between two adjacent sides of an equilateral triangle is 60°
∴  Area of sector with angle ∠A = 60°.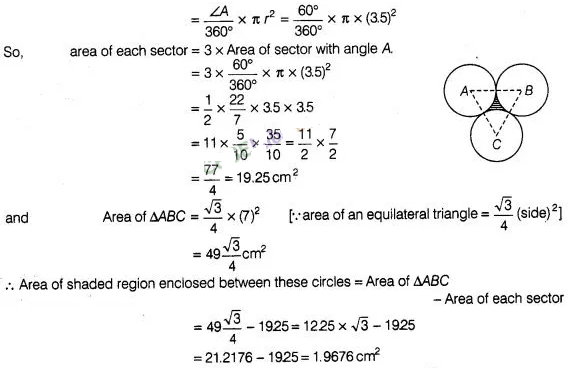

Hence, the required area enclosed between these circles is 1.967 cm² (approx).

Question 8:
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
Solution:
Let the central angle of the sector be θ.
Given that, radius of the sector of a circle (r) = 5 cm^.

Hence, required area of the sector of a circle is 8.75 cm²

Question 9:
Four circular cardboard pieces of radii 7 cm are placed on a paperin such a way that each piece touches other two pieces. Find the area of the portion enclosed between these pieces.
Solution:
Given that, four circular cardboard pieces arc placed on a paper in such a way that each piece touches other two pieces.
Now, we join centre of all four circles to each other by a line segment. Since, radius of each circle is 7 cm.
So,           AB = 2 x Radius of circle
= 2×7 = 14cm
⇒             AB = BC = CD = AD = 14cm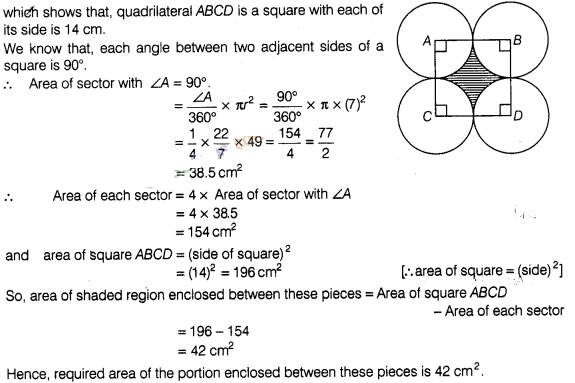

Hence, required area of the portion enclosed between these pieces is 42 cm².

Question 10:
On a square cardboard sheet of area 784 cm², four congruent circular plates of maximum size are placed such that each circular plate touches the other two plates and each side of the square sheet is tangent to two circular plates. Find the area of the square sheet not covered by the circular plates.
Solution:

Question 11:
Floor of a room is of dimensions 5m x 4m and it is covered with circular tiles of diameters 50 cm each as shown infigure. Find area of floor that remains uncovered with tiles, (use π = 3.14)
Solution: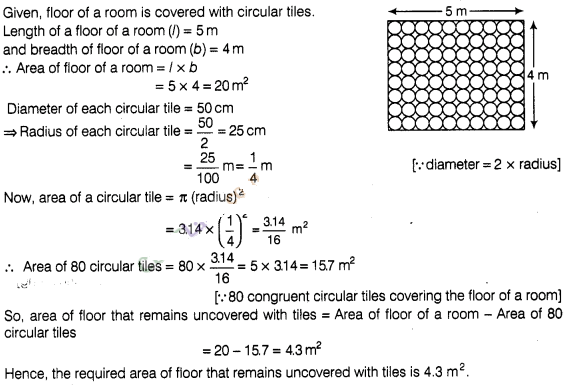

Question 12:
All the vertices of a rhombus lie on a circle. Find the area of the rhombus, if area of the circle is 1256 cm², (use π = 3.14)
Solution:
Let the radius of the circle be r.

Since, all the vertices of a rhombus lie on a circle that means each diagonal of a rhombus must pass through the centre of a circle that is why both diagonals are equal and same as the diameter of the given circle.

Hence, the required  area of rhombus is 800 cm²

Question 13:
An archery target has three regions formed by three concentric circles as shown in figure. If the diameters of the concentric circles are in the ratio 1:2:3, then find the ratio of the areas of three regions.

Solution:
Let the diameters of concentric circles be k, 2k and 3k.

Question 14:
The length of the minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6 : 05 am and 6 : 40 am
Solution:

Question 15:
Area of a sector of central angle 200° of a circle is 770 cm². Find the length of the corresponding arc of this sector.
Solution:
Let the radius of the sector AOBA be r.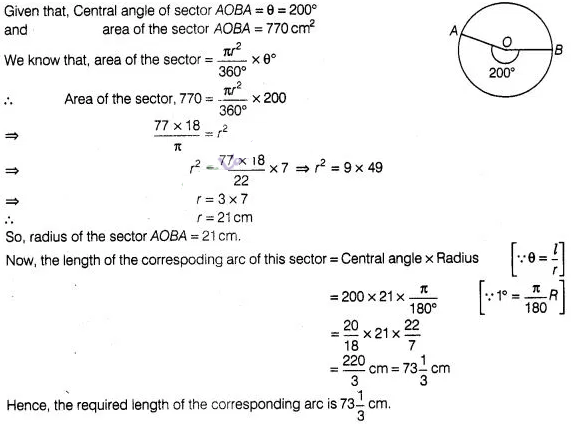

Question 16:
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
Solution:
Let the lengths of the corresponding arc be l₁ and l₂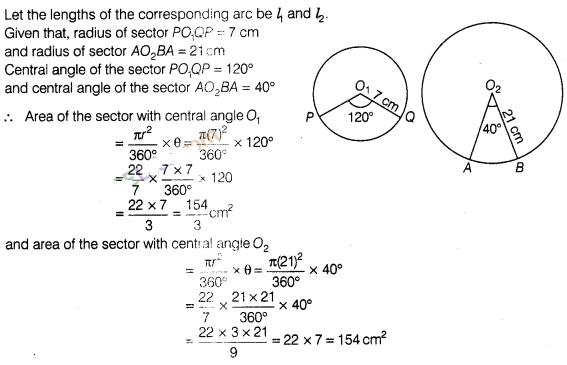


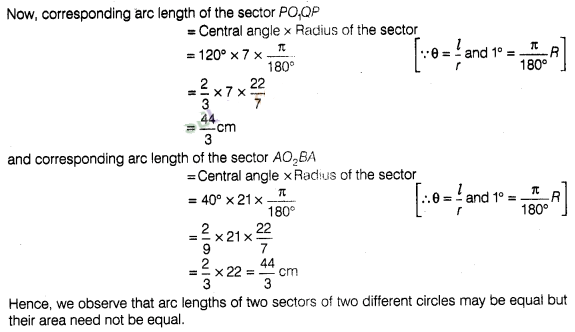
Hence, we observe that arc lengths of two sectors of two different circles may be equal but their area need not be equal.

Question 17:
Find the area of the shaded region given in figure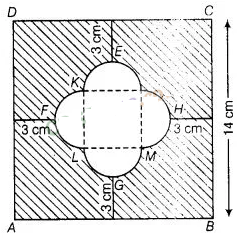

Solution:
Join JK, KL, LM and MJ,
Their are four equally semi-circles and LMJK formed a square.

Hence, the required of the shaded region is (180 – 8π)cm².

Question 18:
Find the number of revolutions made by a circular wheel of area 1.54 m² in rolling a distance of 176 m.
Solution:
Let the number of revolutions made by a circular wheel be n and the radius of circular wheel be r.

Hence, the required number of revolutions made by a circular wheel is 40.

Question 19:
Find the difference of the areas of two segments of a circle formed by a chord of length 5 cm subtending an angle of 90° at the centre.
Solution:
Let the radius of the circle be r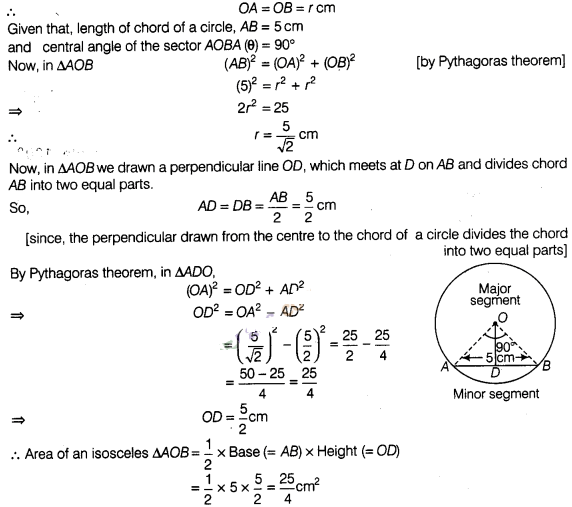

Question 20:
Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
Solution:
Given that, radius of the circle (r) = 21 cm and central angle of the sector AOBA (θ) = 120°

Hence, the required difference of two sectors is 462 cm²