Chapter 1 Real Numbers

NCERT Exemplar Class 10 Maths Chapter 1 Real Numbers

Exercise 1.1
Choose the correct answer from the given four options in the following questions:

Question 1
For some integer m, every even integer is of the form
(A) m
(B) m + 1
(C) 2m
(D) 2m +1
Solution:
(C) We know that, even integers are 2, 4, 6,….
So, it can be written in the form of 2m.
where, m = integer or m = …, -1, 0, 1, 2, 3, ….
∴ 2m = …., -2, 0, 2, 4, 6,….

Question 2
For some integer q, every odd integer is of the form
(A) q
(B) q+1
(C) 2q
(D) 2q + 1
Solution:
(D) We know that, odd integers are 1, 3, 5,…
So, it can be written in the form of 2q + 1
where q = integer
or q = …., -2, -1, 0, 1, 2, 3, ….
∴ 2q + 1 = …., -3, -1,1, 3, 5,….

Question 3
n² – 1 is divisible by 8, if n is
(A) an integer
(B) a natural number
(C) an odd integer
(D) an even integer
Solution:
(C) Let a = n² – 1 Here n can be even or odd.

Case I : n is even, i.e., n = 2k, where k is an integer.
⇒ a = (2k)² – 1
⇒ a = 4k² – 1
At k = -1, a = 4(-1)2 – 1 = 4 – 1 = 3,
which is not divisible by 8
At k = 0, a = 4(0)² – 1 = 0 – 1 = -1,
which is not divisible by 8
At k = 1, a = 4(1)(1 + 1) = 8,
which is divisible by 8.
Hence, we can conclude from above two cases that if n is odd, then n² – 1 is divisible by 8.

Question 4
If the HCF of 65 and 117 is expressible in the form 65m – 117, then the value of m is
(A) 4
(B) 2
(C) 1
(D) 3
Solution:
(B) By Euclid’s division algorithm, b = aq + r, 0 ≤ r < a
[∵ dividend = divisor x quotient + remainder]
⇒ 117 = 65 x 1 + 52
⇒ 65 = 52 x 1 + 13
⇒ 52 = 13 x 4 + 0
∴ HCF (65, 117) = 13 …(i)
Also, given that, HCF (65,117) = 65m -117 …(ii)
From (i) and (ii),
65m – 117 =13
⇒ 65m = 130
⇒ m = 2

Question 5
The largest number which divides 70 and 125, leaving remainders 5 and 8, respectively, is
(A) 13
(B) 65
(C) 875
(D) 1750
Solution:
(A) Since 5 and 8 are the remainders of 70 and 125, respectively.
Thus, after subtracting these remainders from the numbers,
we have the numbers (70 – 5) = 65, (125 – 8) = 117
which are divisible by the required number.
Now, required number = HCF of 65 and 117 For this, 117 = 65 x 1 + 52 [ ∵ dividend = divisor x quotient + remainder]
⇒ 65 = 52 x 1 + 13
⇒52 = 13 x 4 + 0
∴ HCF (65, 117) = 13
Hence, 13 is the largest number which divides 70 and 125, leaving remainders 5 and 8 respectively.

Question 6
If two positive integers a and b are written as a = x³y² and b = xy³; x, y are prime numbers, then HCF (a, b) is
(A) xy
(B) xy²
(C) x³y³
(D) x²y²
Solution:
(B) Given that, a = x³y² = x × x × x × y × y and b = xy³ = x × y × y × y
∴ HCF of a and b = HCF (x³y², xy³)
= x × y × y = xy²
[Since, HCF is the product of the smallest power of each common prime factor involved in the numbers]

Question 7
If two positive integers p and q can be expressed as p = ab², and q = ab; a, b being prime numbers, then LCM (p, q) is
(A) ab
(B) a²b²
(C) a³b²
(D) a³b³
Solution:
(C) Given that, p = ab² = a × b × b
and q = a³b = a × a × a × b
LCM of p and q = LCM (ab², a³b) = a x b x b x a x a = a³b²
[Since, LCM is the product of the greatest power of each prime factor involved in the numbers]

Question 8
The product of a non-zero rational and an irrational number is
(A) always irrational
(B) always rational
(C) rational or irrational
(D) one
Solution:
(A) Product of a non-zero rational and an irrational number is always irrational.

Question 9
The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is
(A) 10
(B) 100
(C) 504
(D) 2520
Solution:
Factors of numbers from 1 to 10
1 = 1
2 = 1 x 2
3 = 1 x 3
4 = 1 x 2 x 2
5 = 1 x 5
6 = 1 x 2 x 3
7 = 1 x 7
8 = 1 x 2 x 2 x 2
9 = 1 x 3 x 3
10 = 1 x 2 x 5
∴ LCM of numbers from 1 to 10
= LCM(1, 2, 3, 4, 5, 6, 7, 8, 9,10)
=1 x 2 x 2 x 2 x 3 x 3 x 5 x 7
= 2520

Question 10
The decimal expansion of the rational number will \(\frac { 14587 }{ 1250 }\) terminate after:
(A) one decimal place
(B) two decimal places
(C) three decimal places
(D) four decimal places
Solution: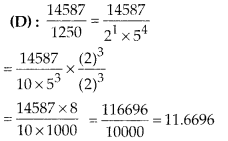

Hence, given rational number will terminate after four decimal places.

Exercise 1.2

Question 1
Write whether every positive integer can be of the form 4q + 2, where q is an integer. Justify your answer.
Solution:
No. By Euclid’s lemma, b = aq + r, 0 ≤ r < a
[∵ dividend = divisor x quotient + remainder]
Here, b is any positive integer and a = 4
∴ b = 4q + r for 0 ≤ r < 4
i.e., r = 0,1, 2, or 3
So, every positive integer can be of the form 4q, 4q + 1, 4q + 2 or 4q + 3.

Question 2
“The product of two consecutive positive integers is divisible by 2”. Is this statement true or false? Give reasons.
Solution:
True
Two consecutive integers can be n, (n + 1). So, one integer out of these two must be divisible by 2. Hence, product of two consecutive integers is divisible by 2.

Question 3
“The product of three consecutive positive integers is divisible by 6”. Is this statement true or false? Justify your answer.
Solution:
True
Three consecutive integers can be n, (n + 1) and (n +2).
So, one integer of these three must be divisible by 2 and another one must be divisible by 3. Hence, product of three consecutive integers is divisible by 6.

Question 4
Write whether the square of any positive integer can be of the form 3m + 2, where m is a natural number. Justify your answer.
Solution:
No. By Euclid’s lemm a, b = aq + r, 0 ≤ r < a
Here, b is any positive integer and a = 3 ⇒ b = 3q + r for 0 ≤ r < 3
So, any positive integer is of the form 3q, 3q + 1 or 3q + 2
Now, (3q)² = 9q² = 3m [where, m = 3q²]
and (3q + l)² = 9q² + 6q + 1 = 3(3q² + 2q) + 1
= 3m + 1 [where, m = 3q² + 2q]
Also, (3q + l)² = 9q² + 12q + 4
[∵ (a + b)² = a² + 2 ab + b²]
= 9q² + 12q + 3 + 1 = 3(3q² + 4q + l) + l
= 3m + 1 [where, m = 3q² + 4q + 1]
which is in the form of 3m and 3m + 1. Hence, square of any positive integer cannot be of the form 3m + 2.

Question 5
A positive integer is of the form 3q + 1, q being a natural number. Can you write its square in any form other than 3m + 1, i.e., 3m or 3m + 2 for some integer m? Justify your answer.
Solution:
No. Let a be any positive integer of the form 3q + 1, where q is a natural number.
Now, a = 3q + 1
Squaring both sides, we get a² = (3 q + 1)² = 9q² + 1 +6q = 3(3 q2 + 2q) + 1 = 3 m + 1,
where m = 3q² + 2q is an integer.
Hence, square of a positive integer of the form 3q + 1 is always in the form 3m + 1 for some integer m.

Question 6
The numbers 525 and 3000 are both divisible only by 3, 5, 15, 25 and 75. What is HCF (525, 3000)? Justify your answer.
Solution:
By Euclid’s lemma,
3000 = 525 x 5 + 375
[∵ dividend = divisor x quotient + remainder]
525 = 375 x 1 + 150 375 = 150 x 2 + 75 150 = 75 x 2 + 0
∴ HCF (525, 3000) = 75
The numbers 3, 5,15, 25 and 75 divides the numbers 525 and 3000 that means these all are common factors of 525 and 3000.
The highest common factor among these is 75.

Question 7
Explain why 3 x 5 x 7 + 7 is a composite number.
Solution:
We have, 3 x 5 x 7 +7 = 7 [3 x 5 +1], which is not a prime number because it has a factor 7,
i.e. it has more than two factors.
Hence, it is a composite number.

Question 8
Can two numbers have 18 as their HCF and 380 as their LCM? Give reasons.
Solution:
No, because HCF is always a factor of LCM but here 18 is not a factor of 380.

Question 9
Without actually performing the long division, find if \(\frac { 987 }{ 10500 }\) will have terminating or non-terminating (repeating) decimal expansion.
Give reasons for your answer.
Solution: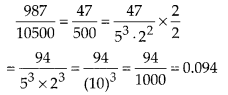

After simplification denominator has factor 5³. 2³ and which is of the type 2^m . 5ⁿ.
So, this is terminating decimal.

Question 10
A rational number in its decimal expansion is 327.7081. What can you say about the prime factors of q, when this number is expressed in
the form \(\frac { p }{ q }\) ? Give reasons.
Solution:
327.7081 is terminating decimal number.
So, it represents a rational number and also its denominator must have the form 2^m x 5ⁿ.
Thus, 327.7081 = \(\frac { 3277081 }{ 10000 }\) = \(\frac { p }{ q }\) (say)
∴ q = 10⁴ = 2 x 2 x 2 x 2 x 5 x 5 x 5 x 5 = 2⁴ x 5⁴ = (2 x 5)⁴
Hence, the prime factors of q are 2 and 5.

Exercise 1.3

Question 1
Show that the square of any positive integer is either of the form 4q or 4q + 1 for some integer q.
Solution:
Let a bean arbitrary positive integer. Then by Euclid’s division algorithm, corresponding to the positive integers n and 4, there exists non-negative integers n: and r,
such that
a = 4m + r, where 0 ≤ r < 4
⇒ a² =16m² ÷ r²– 8mr. where 0 ≤ r < 4 …(i)
[∵ (a + b)² = a² + 2ab + b²]

Case 1 : When r = 0, then putting r = 0 in
eq. (i), we get
a² = 16m² = 4(4m²) = 4q
where, q = 4m² is an integer.

Case II: When r = 1, then putting r = 1 in
eq. (i), we get
a² = 16m² + 1 + 8m
= 4(4m² + 2 in) + 1 = 4q + 1
where, q = (4m² + 2m) is an integer.

Case III : When r = 2, then putting r = 2 in eq. (i), we get
a² = 16m² + 4 + 16m = 4(4m² + 4m + 1) = 4 q
where, q = (4m² + 4m + 1) is an integer.

Case IV : When r = 3, then putting r = 3 in eq. (i), we get
a² = 16 m² + 9 + 24 m = 16m² + 24 m + 8 + 1 = 4(4m² + 6m + 2) + 1 = 4q + 1
where, q = (4m² + 6m + 2) is an integer.
Hence, the square of any positive integer is either of the form 4q or 4q + 1 for some integer q.

Question 2
Show that cube of any positive integer is of the form 4m, 4m + 1 or 4m + 3, for some integer m.
Solution:
Let a be an arbitrary positive integer. Then, by division algorithm, corresponding to the positive integers a and 4, there exist non-negative integers q and r such that
a = 4q + r, where 0 ≤ r < 4
⇒ a³ = (4q + r)³= 64q³ + r³ + 12qr² + A8q² r
[∵ (a + b)³ = a³ + b³ + 3ab² + 3a²b)
⇒ a³ = (64q³ + 48q²r + 12qr²) + r³ … (i)
where 0 ≤ r < 4

Case I : When r = 0, then putting r = 0 in eq. (i), we get
a³ = 64 q³ = A(16q³)
⇒ a³ = 4m, where, m = 16q³ is an integer.

Case II : When r = 1, then putting r = 1 in eq. (i), we get
a³ = 64q³ + 48q² + 12q + 1
= A(16q³ + 12q² + 3q) + 1 = 4m +1
where, m = (16q³ + 12q² + 3q) is an integer.

Case III : When r = 2, then putting r = 2 in eq. (i), we get
a³ = 64 q³ + 96 q² + 48q + 8
= 4(16q³ + 24q² + 12q + 2)
= 4m
where, m = (16q³ + 24q² +12q + 2) is an integer.

Case IV : When r = 3, then putting r = 3 in eq. (i), we get
a³ = 64q³ + 144q² + 108q + 27
= 64 q³ + 144q² + 108 q + 24 + 3
= A(16q³ + 36 q² + 27q + 6) + 3
= 4m + 3
where, m = (16q³ + 36q² + 27q + 6) is an integer. Hence, the cube of any positive integer is of the form 4m, 4m + 1 or 4m + 3 for some integer m.

Question 3
Show that the square of any positive integer cannot be of the form 5q + 2 or 5q + 3 for any integer q.
Solution:
Let a be an arbitrary positive integer.
Then, by Euclid’s division algorithm, corresponding to the positive integers a and 5, there exist non-negative integers m and r such that
a = 5m + r, where 0 ≤ r < 5
⇒ a² = (5m + r)² = 25 m² + r² + 10mr
[∵ (a + b)² = a² + 1ab + b²]
⇒ a² = 5(5m²+ 2mr) + r², where 0 < r < 5 …(i)

Case I : When r = 0, then putting r = 0 in eq. (i), we get
a² = 5(5 m²) = 5 q where q = 5m² is an integer.

Case II : When r = 1, then putting r = 1 in eq. (i), we get
a² = 5(5 m² + 2m) + 1
⇒ a² = 5q + 1
where q = (5m² + 2m) is an integer.

Case III : When r = 2, then putting r = 2 in eq. (i), we get
a² = 5(5 m² + 4m) + 4 = 5q + 4 where q = (5m² + 4m) is an integer.

Case IV : When r = 3, then putting r = 3 in eq. (i), we get
a² = 5(5m² + 6m) + 9 = 5(5 m² + 6m) + 5 + 4 = 5(5 m² + 6m + 1) + 4 = 5q + 4 where, q = (5m² + 6m + 1) is an integer.

Case V : When r = 4, then putting r = 4 in eq. (i), we get
a² = 5(5m²+ 8m) + 16 = 5(5 m² + 8m) + 15 + 1
⇒ a² = 5(5m² + 8m + 3) + 1 = 5q + 1 where q = (5m² + 8m + 3) is an integer.
Hence, the square of any positive integer cannot be of the form 5q + 2 or 5q + 3 for any integer q.

Question 4
Show that the square of any positive integer cannot be of the form 6m + 2 or 6m + 5 for any integer m.
Solution:
Let a be an arbitrary positive integer, then by Euclid’s division algorithm, corresponding to the positive integers a and 6, there exist non-negative integers q and r such that a = 6q + r, where 0 ≤ r < 6
⇒ a² = (6q + r)² = 36 q² + r² + 12qr
[∵ (a + b)² = a² + 2 ab + b²]
⇒ a² = 6(6q² + 2qr) + r² … (i)
where 0 ≤ r < 6

Case I: When r = 0, then putting r = 0 in eq. (i), we get
a² = 6(6 q² ) = 6 m
where m = 6q² is an integer.

Case II : When r = 1, then putting r = 1 in eq. (i), we get
a² = 6(6q² + 2 q) + 1 = 6 m + 1
where m = (6q² + 2q) is an integer.

Case III : When r = 2, then putting r = 2 in eq. (i), we get
a² = 6(6q² + 4q) + 4 = 6m + 4
where m = (6q² + 4q) is an integer.

Case IV : When r = 3, then putting r = 3 in eq. (i), we get
a² = 6(6q² + 6q) + 9 = 6(6q² + 6 q) + 6 + 3
⇒ a² = 6(6 q² + 6q + 1) + 3 = 6m + 3
where m = (6q² + 6q + 1) is an integer.

Case V : When r = 4, then putting r = 4 in eq. (i), we get
a² = 6(6 q² + 8 q) + 16 = 6(6 q² + 8q) + 12 + 4
⇒ a² = 6(6 q² + 8q + 2) + 4 = 6m + 4
where m = (6q² + 8q + 2) is an integer.

Case VI : When r = 5, then putting r = 5 in eq. (i), we get
a² = 6(6 q² + 10q) + 25 = 6(6 q² + 10 q) + 24 + 1
⇒ a² = 6(6 q² + 10 q + 4) + 1 = 6m + 1
where m = (6q² + 10q + 4) is an integer.
Hence, the square of any positive integer cannot be of the form 6m + 2 or 6m + 5 for any integer m.

Question 5
Show that the square of any odd integer is of the form 4q + 1, for some integer q.
Solution:
By Euclid’s division algorithm, we have a = bm + r, where 0 ≤ r < b … (i)
On putting b = 4 in eq. (i), we get
a = 4m + r, where 0 ≤ r < 4, i.e., r = 0,1, 2, 3 If r = 0
⇒ a = 4m, 4m is divisible by 2
⇒ 4m is even.
If r = 1 ⇒ a = 4m + 1, (4m + 1) is not divisible by 2.
If r = 2 ⇒ a = 4m + 2 = 2(2 m + 1), 2(2 m + 1) is divisible by 2 ⇒ 2(2m + 1) is even.
If r = 3 ⇒ a = 4m + 3, (4m + 3) is not divisible by 2.
So, for any positive integer m, (4m + 1) and (4m + 3) are odd integers.
Now, a² = (4m + 1)² = 16m² + 1 + 8m
[∵ (a + b)² = a² + 2ab + b²] = 4(4m² + 2m) + 1 = 4q + 1
It is a square which is of the form 4q +1, where q = (4m² + 2m) is an integer, and a²= (4m + 3)² = 16m² + 9 + 24m
[∵ (a + b)² = a² + 2ab + b²]
= 4(4m² + 6m + 2) + 1 = 4g + 1 It is a square which is of the form 4q +1, where q = (4m² + 6m + 2) is an integer.
Hence, for some integer q, the square of any odd integer is of the form 4q + 1.

Question 6
If n is an odd integer, then show that n² – 1 is divisible by 8.
Solution:
Let a = n² – 1 … (i)
Given that, n is an odd integer.
∴ n = 1, 3, 5,….
From eq. (i), at n = 1, a = (1)²– 1 = 1 – 1 = 0 which is divisible by 8.
From eq. (i), at n = 3, a = (3)² – 1 = 9 – 1 = 8 which is divisible by 8 From eq. (i), at n = 5
a = (5)² – 1 = 25 – 1= 24 = 3 x 8 which is divisible by 8 From eq. (i), at n = 7,
a = (7)² – 1= 49 – 1= 48 = 6 x 8 which is divisible by 8
Hence, (n² – 1) is divisible by 8, where n is an odd integer.

Question 7
Prove that if x and y are both odd positive integers, then x² + y² is even but not divisible by 4.
Solution:
Let x = 2m + 1 and y = 2m + 3 are odd positive integers, for every positive integer m.
Then, x² + y² = (2m + 1)² + (2m + 3)² = 4m² + 1 + 4m + 4m² + 9 + 12m
[∵ (a + b)² = a² + 2ab + b²]
= 8m² + 16m + 10
= 2(4m² + 8m + 5) or 4(2m² + 4m + 2) + 2
Hence, x² + y² is even for every positive integer m but not divisible by 4.

Question 8
Use Euclid’s division algorithm to find the HCF of 441, 567,693.
Solution:
Let a = 693, b = 567 and c = 441
By Euclid’s division algorithm,
a = bq + r … (i)
[∵ dividend = divisor x quotient + remainder]
First we take, a = 693 and b = 567 and find their HCF.
693 = 567 x 1 + 126
567 = 126 x 4 + 63
126 = 63 x 2 + 0
∴ HCF (693, 567) = 63
Now, we take c = 441 and (say) d = 63 then find their HCF.
Again, using Euclid’s division algorithm, c = dq + r
⇒ 441=63 x 7 + 0
∴ HCF (693, 567, 441) = 63

Question 9
Using Euclid’s division algorithm, find the largest number that divides 1251, 9377 and 15628 leaving remainders 1, 2 and 3, respectively.
Solution:
Since, 1, 2 and 3 are the remainders of 1251, 9377 and 15628, respectively. Thus, after subtracting these remainders from the numbers, we have the numbers 1251 – 1 = 1250, 9377 – 2 = 9375 and 15628 – 3 = 15625
which are divisible by the required number. Now, required number
= HCF (1250, 9375, 15625)
By Euclid’s division algorithm,
a = bq + r … (i)
[∵ dividend = divisor x quotient + remainder]
Let a = 15625 and b = 9375
15625 = 9375 x 1 + 6250 [from eq. (i)]
⇒ 9375 = 6250 x 1 +3125
⇒ 6250 = 3125 x2 + 0
∴ HCF (15625, 9375) = 3125
Now, we take c = 1250 and d = 3125, then again using Euclid’s division algorithm, d = cq + r
⇒ 3125 = 1250 x 2 + 625
⇒ 1250 = 625 x 2 + 0
∴ HCF (1250, 9375,15625) = 625
Hence, 625 is the largest number which divides 1251, 9377 and 15628 leaving remainders, 1, 2 and 3, respectively.

Question 10
Prove that √3 + √5 is irrational.
Solution:
Let us suppose √3 + √5 is rational.
Let √3 + √5 = a , where a is rational.
Therefore, √3 = a- √5 On squaring both sides, we get
(√3)² = (a – √5)²
⇒ 3 = a² + 5 – 2a√5
[∵ (a – b)² = a² + b² – 2ab]
⇒ 2a√5 = a² + 2
Therefore, √5 = \(\frac { { a }^{ 2 }+2 }{ 2a }\) , which is a contradiction as the right hand side is rational number while √5 is irrational.
Hence, √3 + √5 is irrational.

Question 11
Show that 12ⁿ cannot end with the digit 0 or 5 for any natural number n.
Solution:
If any number ends with the digit 0 or 5,
it is always divisible by 5.
If 12ⁿ ends with the digit zero or five it must be divisible by 5.
This is possible only if prime factorisation of
12ⁿ contains the prime number 5.
Now, 12 = 2 x 2 x 3 = 2² x 3
12ⁿ = (2² x 3)ⁿ = 2²ⁿ x 3ⁿ
since, there is no term containing 5.
Hence, there is no value of n ∈ N for which 12ⁿ ends with the digit zero or five.

Question 12
On a morning walk, three persons step off together and their steps measure 40 cm, 42 cm and 45 cm, respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
Solution:
We have to lind the LCM of 40 cm, 42 cm and 45 cm to get the required minimum distance.
For this, 40 = 2 x 2 x 2 x 5
42 = 2 x 3 x 7
and 45 = 3 x 3 x 5
∴ LCM(40,42,45) = 2 x 3 x 5 x 2 x 2 x 3 x 7
= 2520
Minimum distance each should walk is 2520 cm so that each can cover the same distance in complete steps.

Question 13
Write the denominator of the rational number \(\frac { 257 }{ 5000 }\) in the form 2^m x 5ⁿ, where m, n are non-negative integers. Hence, write its decimal expansion, without actual division.
Solution:
Denominator of the rational number \(\frac { 257 }{ 5000 }\) is 5000.
Now, 5000 = 2 x 2 x 2 x 5 x 5 x 5 x 5
= (2)³ x (5)⁴, which is of the type 2^m x 5ⁿ where m = 3 and n = 4 are non-negative integers.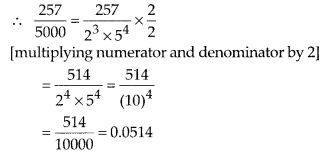

Hence, 0.0514 is the required decimal expansion of the rational number \(\frac { 257 }{ 5000 }\) and it is also a terminating decimal number.

Question 14
Prove that √p + √q is irrational, where p,q are primes.
Solution:
Let us suppose that √p + √q is rational.
Again, let √p + √q = a , where a is rational.
Therefore, √q = a – √p
On squaring both sides, we get q = a² + p – 2 a√p
[∵ (a – b)² = a² + b² – 2ab]
Therefore, \(\sqrt { p } =\quad \frac { { a }^{ 2 }+p-q }{ 2a }\)
which is a contradiction as the right hand side is rational number while √p is irrational, since p is a prime number.
Hence, √p + √q is irrational.

Exercise 1.4

Question 1
Show that the cube of a positive integer of the form 6q + r, q is an integer and r = 0, 1, 2, 3, 4, 5 is also of the form 6m + r.
Solution:
Let a be an arbitrary positive integer. Then,
by Euclid’s division algorithm, corresponding to the positive integers a and 6, there exist non-negative integers q and r such that
a = 6q + r, where 0 ≤ r < 6
⇒ a³ = (6q + r)³ = 216q³ + r³ + 3 . 6q . r(6q + r)
[∵ (a + b)³ = a³ + b³ + 3ab(a + b)]
⇒ a³ = (216q³ + 108q²r + 18qr²) + r³ … (i)
where 0 < r < 6

Case I : When r = 0, then putting r = 0 in eq. (i), we get
a³ = 216 q³ = 6(36q³) = 6m
where, m = 36q³ is an integer

Case II : When r = 1, then putting r = 1 in eq. (i), we get
a³ = (216 q³ + 108 q² + 18 q) + 1 = 6(36 q³ + 18 q² + 3q) + 1
⇒ a³ = 6m + 1,
where m = (36q³ + 18q² + 3q) is an integer.

Case III : When r = 2, then putting r = 2 in eq. (i), we get
a³ = (216 q³ + 216 q² + 72q) + 8 a³
= (216 q³ + 216 q² + 72q + 6) + 2
⇒ a³ = 6(36q³ + 36q² + 12q + 1) + 2
= 6m + 2 where, m = (36q³ + 36q²+ 12q + 1) is an integer.

Case IV : When r = 3, then putting r = 3 in eq. (i), we get
a³ = (216 q³+ 324q² + 162 q) + 27
= (216 q³ + 324q² + 162 q + 24) + 3
= 6(36 q³ + 54 q² + 27q + 4) + 3 = 6m + 3 where, m = (36q³ + 54q² + 27q + 4) is an integer.

Case V : When r = 4, then putting r = 4 in eq. (i), we get
a³ = (216q³ + 432q² + 288q) + 64 = 6(36 q³ + 72q² + 48 q) + 60 + 4 a³ = 6(36 q³ + 72q² + 48 q + 10) + 4 = 6m + 4
where, m = (36q³ + 72q² + 48q +10) is an integer.

Case VI : When r = 5, then putting r = 5 in eq. (i), we get
a3 = (216 q3 + 540q2 + 450q) + 125⇒ a3 = (216 q³+ 540q² + 450q) + 120 + 5
⇒ a³ = 6(36q³ + 90q² + 75q + 20) + 5
⇒ a³ = 6m + 5
where, m = (36 q³ + 90 q² + 75q + 20) is an integer.
Hence, the cube of a positive integer of the form 6q + r, q is an integer and r = 0,1, 2, 3, 4, 5 is also of the form 6m, 6m + 1, 6m + 2, 6m + 3, 6m + 4 and 6m + 5, i.e., 6m + r.

Question 2
Prove that one and only one out of n, n + 2 and n + 4 is divisible by 3, where n is any positive integer.
Solution:
On dividing n by 3, let q be the quotient and r be the remainder.
Then, by Euclid’s division algorithm, n = 3q + r, where 0 ≤ r < 3
⇒ n = 3q + r, where r = 0,1, 2
⇒ n = 3q or n = 3q + 1 or n = 3q + 2

Case I: If n = 3q which is divisible by 3.
But n + 2 and n + 4 are not divisible by 3.
So, in this case, only n is divisible by 3.

Case II: If n = 3q + 1, then (n + 2) = 3q + 3 = 3(q + 1),
which is divisible by 3 but n and n + 4 are not divisible by 3.
So, in this case, only (n + 2) is divisible by 3.

Case III: If n = 3q + 2, then (n + 4) = 3q + 6 = 3(q + 2),
which is divisible by 3 but n and (n + 2) are not divisible by 3.
So, in this case, only (n + 4) is divisible by 3.
Hence, one and only one out of n, (n + 2) and (n + 4) is divisible by 3.

Question 3
Prove that one of any three consecutive positive integers must be divisible by 3.
Solution:
Let three consecutive positive integers are n, n +1 and n + 2.
On dividing n by 3, let q be the quotient and r be the remainder.
Then, by Euclid’s division algorithm,
n = 3q + r, where 0 ≤ r < 3
⇒ n = 3q or n = 3q + 1 or n = 3q + 2

Case I: If n = 3q, which is divisible by 3
but (n + 1) and (n + 2) are not divisible by 3.
So, in this case, only n is divisible by 3.

Case II: If n = 3q + 1, then n + 2 = 3q + 3 = 3(q + 1) which is divisible by 3
but n and (n + 1) are not divisible by 3.
So, in this case, only (n + 2) is divisible by 3.

Case III: If n – 3q + 2, then n + 1 = 3q + 3 = 3(q + 1) which is divisible by 3
but n and (n + 2) are not divisible by 3.
So, in this case, only (n + 1) is divisible by 3.
Hence, one of any three consecutive positive integers must be divisible by 3.

Question 4
For any positive integer n, prove that n – n is divisible by 6.
Solution:
Let a = n³ – n
⇒ a = n – (n² – 1)
⇒ a = n – (n – 1)(n + 1)
[∵ (a² – b²) = (a – b)(a + b)]
⇒ a = (n – 1) n (n + 1)
We know that, if a number is divisible by both 2 and 3, then it is also divisible by 6.
n – 1, n and n + 1 are three consecutive integers.
Now, a = (n – 1 )n (n + 1) is product of three consecutive integers.
So, one out of these must be divisible by 2 and another one must be divisible by 3.
Therefore, a is divisible by both 2 and 3.
Thus, a = n³ – n is divisible by 6.

Question 5
Show that one and only one out of n, n + 4, n + 8,n+ 12 and n + 16 is divisible by 5, where n is any positive integer.
[Hint: Any positive integer can be written in the form 5q, 5q+1 ,5q + 2, 5q + 3, 5q +4 ].
Solution:
On dividing n by 5, let q be the quotient and r be the remainder.
Then n = 5q + r, where 0 ≤ r < 5
⇒ n = 5q + r, where r = 0,1, 2, 3, 4
⇒ n = 5q or 5q + 1 or 5q + 2 or 5q + 3 or 5q + 4

Case I: If n = 5q, then only n is divisible by 5.
Case II: If n = 5q + 1, then n + 4 = 5q + 1+ 4 = 5q + 5 = 5(q + 1) which is divisible by 5
So, in this case, only (n + 4) is divisible by 5

Case III: If n = 5q + 2, then
n + 8 = 5q + 10 = 5 (q + 2)
which is divisible by 5.
So, in this case, only (n + 8) is divisible by 5.

Case IV : If n = 5q + 3,
then n + 12 = 5q + 3 + 12 = + 15 = 5(q + 3)
which is divisible by 5
So, in this case, only (n + 12) is divisible by 5.

Case V : If n = 5q + 4, then
n + 16 = 5q + 4 + 16 = 5q + 20
= 5(q + 4) which is divisible by 5
So, in this case, only (n + 16) is divisible by 5.
Hence, one and only one out of n, n + 4, n + 8, n + 12 and n + 16 is divisible by 5, where n is any positive integer.